09 - Statystyki opisowe

Skale pomiarowe w statystyce¶

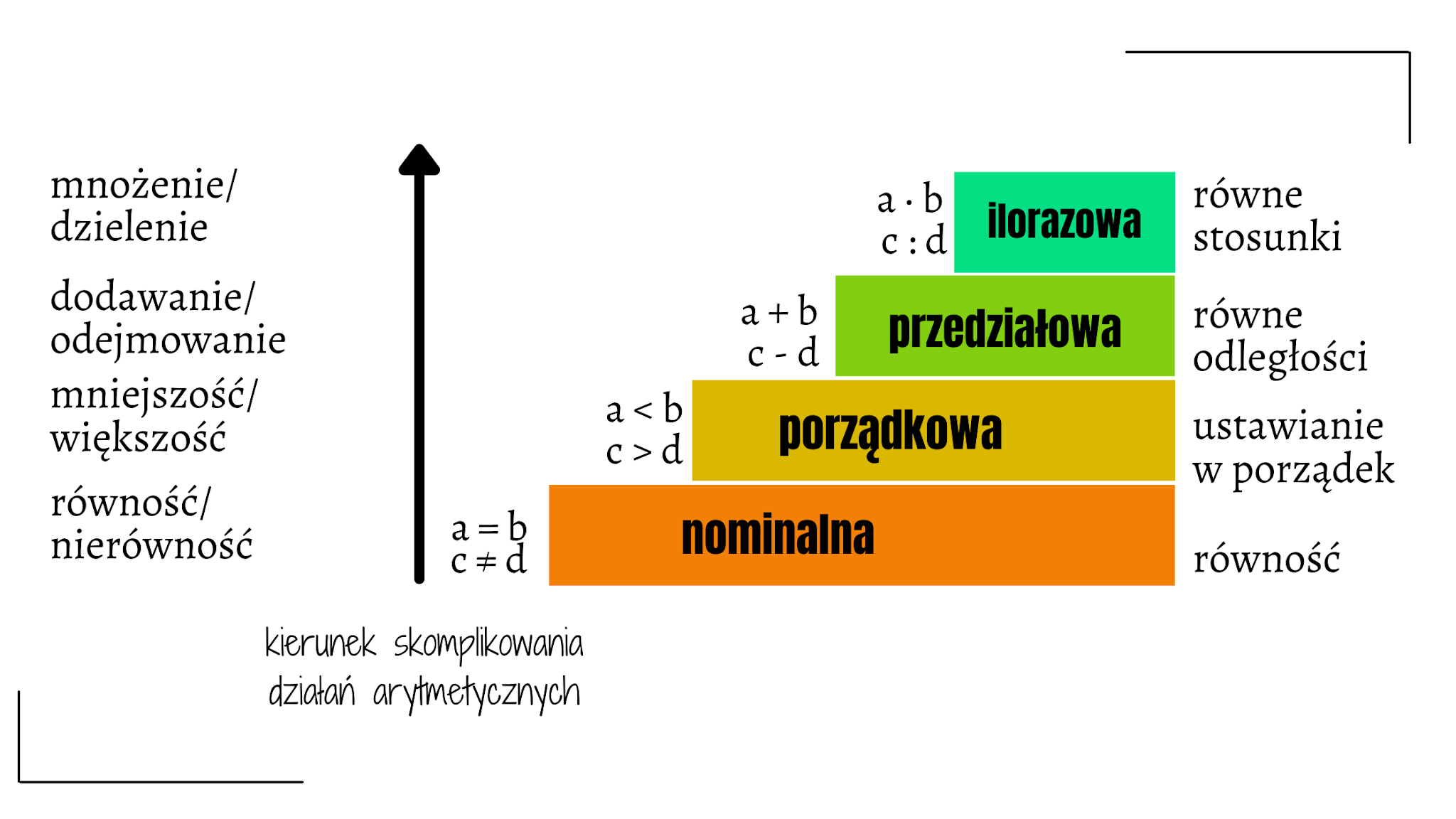
Skale pomiarowe określają, jakie operacje matematyczne i statystyczne można wykonywać na danych. Wyróżniamy cztery podstawowe typy skal:

Skala nominalna (nazewnicza)

Dane służą tylko do nazwania lub kategoryzacji.
Nie da się ustalić porządku między wartościami.
Możliwe operacje: zliczanie, tryb, analiza częstości.

Przykłady:

Typ Pokémona (type_1): “fire”, “water”, “grass” itp.
Gatunek, płeć, kolory.

import pandas as pd
df_pokemon = pd.read_csv("data/pokemon.csv")
df_pokemon["Type 1"].value_counts()

Type 1
Water       112
Normal       98
Grass        70
Bug          69
Psychic      57
Fire         52
Electric     44
Rock         44
Dragon       32
Ground       32
Ghost        32
Dark         31
Poison       28
Steel        27
Fighting     27
Ice          24
Fairy        17
Flying        4
Name: count, dtype: int64

Skala porządkowa

Dane dają się uporządkować, ale odległości między nimi nie są znane.
Możliwe operacje: mediana, kwantyle, testy rangowe (np. Spearmana).

Przykłady:

Poziom siły: “niski”, “średni”, “wysoki”
Oceny jakości: “słaby”, “dobry”, “bardzo dobry”

import seaborn as sns

titanic = sns.load_dataset("titanic")

print(titanic["class"].unique())

['Third', 'First', 'Second']
Categories (3, object): ['First', 'Second', 'Third']

Skala przedziałowa (interwałowa)

Dane są liczbowe, z równymi odstępami, ale brak zera absolutnego.
Można obliczać różnice, średnią, odchylenie standardowe.
Brak sensu dla ilorazów (np. „dwa razy więcej”).

Przykłady:

Temperatura w °C (ale nie w Kelwinach!). Dlaczego? Brak absolutnego zera — zero nie oznacza braku cechy, jest tylko umownym punktem odniesienia. 0°C nie oznacza braku temperatury; 20°C to nie jest 2 x 10°C.
Rok w kalendarzu (np. 1990). Dlaczego? Rok 0 nie oznacza początku czasu; 2000 to nie 2 x 1000.
Czas w systemie godzinowym (np. 13:00). Dlaczego? 0:00 to niebrak czasu, tylko ustalony punkt odniesienia.

Skala ilorazowa (stosunkowa)

Dane liczbowe, mają zero absolutne.
Można wykonywać wszystkie działania matematyczne, także dzielenie.

Nie wszystkie dane liczbowe (numeryczne) są w skali ilorazowej! Przykład: temperatura w stopniach Celsjusza nie jest w skali ilorazowej, bo 0°C nie oznacza braku temperatury. Natomiast temperatura w Kelwinach (K) już tak, ponieważ 0 K to absolutny brak energii cieplnej.

Przykłady:

Wzrost, waga, liczba punktów ataku Pokémona (attack), HP, speed.

df_pokemon[["HP", "Attack", "Speed"]].describe()

Tabela: Skale pomiarowe w statystyce¶

Skala	Przykład	Czy można porządkować?	Równe odstępy?	Zero absolutne?	Przykładowe operacje statystyczne
Nominalna	Typ Pokémona (`fire`, `water` itd.)	❌	❌	❌	Tryb, zliczenia, analiza częstości
Porządkowa	Klasa biletu (`First`, `Second`, `Third`)	✅	❌	❌	Mediana, kwantyle, testy rangowe
Przedziałowa	Temperatura w °C	✅	✅	❌	Średnia, odchylenie standardowe
Ilorazowa	HP, atak, wzrost	✅	✅	✅	Wszystkie operacje matematyczne/statystyki

Wniosek: Rodzaj skali wpływa na wybór metod statystycznych – np. test korelacji Pearsona wymaga danych ilorazowych lub przedziałowych, a test Chi² – danych nominalnych.

Quiz: Skale pomiarowe w statystyce¶

Odpowiedz na poniższe pytania, wybierając jedną poprawną odpowiedź. Rozwiązania znajdziesz na końcu.

1. Która ze skal umożliwia porządkowanie danych, ale nie ma równych odstępów?¶

A) Nominalna
B) Porządkowa
C) Przedziałowa
D) Ilorazowa

2. Przykładem zmiennej w skali nominalnej jest:¶

A) Temperatura w °C
B) Wzrost
C) Typ Pokémona (fire, grass, water)
D) Poziom zadowolenia (niski, średni, wysoki)

3. Która skala nie ma zera absolutnego, ale posiada równe odstępy?¶

A) Ilorazowa
B) Porządkowa
C) Przedziałowa
D) Nominalna

4. Jakie operacje są dozwolone na zmiennych w skali porządkowej?¶

A) Średnia i odchylenie standardowe
B) Tryb i korelacja Pearsona
C) Mediana i testy rangowe
D) Ilorazy i logarytmy

5. Zmienna `"class"` w zbiorze Titanic (`First`, `Second`, `Third`) to przykład:¶

A) Skali nominalnej
B) Skali ilorazowej
C) Skali przedziałowej
D) Skali porządkowej

Statystyka opisowa¶

Statystyka opisowa zajmuje się opisem rozkładu danych w próbie. Statystyki opisowe dają nam podstawowe miary podsumowujące dotyczące zbioru danych. Miary podsumowujące obejmują miary tendencji centralnej (średnia, mediana i tryb) oraz miary zmienności (wariancja, odchylenie standardowe, wartości minimalne/maksymalne, IQR (zakres międzykwartylowy), skośność i kurtoza).

W tym rozdziale¶

Teraz zajmiemy się opisywaniem naszych danych - jak również podstawami statystyki.

Istnieje wiele sposobów na opisanie rozkładu.

Tutaj omówimy:

Miary tendencji centralnej: jaka jest typowa wartość w tym rozkładzie?
Miary zmienności: jak bardzo wartości różnią się od siebie?
Miary skośności: jak silna jest asymetria rozkładu?
Miary kurtozy: jaka jest intensywność występowania wartości skrajnych?
Pomiar zależności między rozkładami za pomocą korelacji liniowych, rangowych.
Pomiar zależności między zmiennymi jakościowymi za pomocą kontyngencji.

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns 
import scipy.stats as stats

%matplotlib inline 
%config InlineBackend.figure_format = 'retina'

Tendencja centralna¶

Tendencja centralna odnosi się do „typowej wartości” w rozkładzie.

Tendencja centralna oznacza wartość centralną, która opisuje rozkład zmiennej. Może być również nazywana środkiem lub lokalizacją rozkładu. Najpopularniejszymi miarami tendencji centralnej są średnia, mediana i moda. Najpopularniejszą miarą tendencji centralnej jest średnia. W przypadku rozkładu skośnego lub gdy istnieje obawa o wartości odstające, preferowana może być mediana. Mediana jest więc bardziej wiarygodną miarą niż średnia.

Istnieje wiele sposobów mierzenia tego, co jest „typowe” - przeciętne:

Średnia arytmetyczna
Mediana (wartość środkowa)
Moda (dominanta)

Dlaczego jest to przydatne?¶

Zbiór danych może zawierać wiele obserwacji.
- Na przykład, $N = 5000$ odpowiedzi ankietowych dotyczących wysokości.
Jednym ze sposobów „opisania” tego rozkładu jest jego wizualizacja.
Ale pomocne jest również zredukowanie tego rozkładu do pojedynczej liczby.

Jest to z konieczności uproszczenie naszego zbioru danych!

Średnia arytmetyczna¶

Średnia arytmetyczna jest zdefiniowana jako suma wszystkich wartości w rozkładzie, podzielona przez liczbę obserwacji w tym rozkładzie.

liczby = [1, 2, 3, 4]
### obliczanie na piechotę...
sum(liczby)/len(liczby)

2.5

Najpopularniejszą miarą tendencji centralnej jest średnia.
Średnia jest również znana jako średnia prosta.
Oznaczana jest grecką literą $µ$ dla populacji i $\bar{x}$ dla próbki.
Możemy znaleźć średnią liczby elementów, dodając wszystkie elementy w zbiorze danych, a następnie dzieląc przez liczbę elementów w zbiorze danych.
Jest to najpopularniejsza miara tendencji centralnej, ale ma ona pewną wadę.
Na średnią wpływa obecność wartości odstających.
Sama średnia nie jest więc wystarczająca do podejmowania decyzji biznesowych.

\bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i

(1)

`numpy.mean`¶

Pakiet numpy posiada funkcję obliczającą średnią na liście lub numpy.ndarray.

np.mean(liczby)

np.float64(2.5)

Obliczanie `średniej` kolumny `pandas`¶

Jeśli pracujemy z DataFrame, możemy obliczyć średnią konkretnych kolumn.

df_gapminder = pd.read_csv("data/viz/gapminder_full.csv")
df_gapminder.head(2)

df_gapminder['life_exp'].mean()

np.float64(59.474439366197174)

Twoja kolej¶

Jak obliczyć „średnią” kolumny „gdp_cap”?

### Twój kod tutaj

Średnia i skośność¶

Skośność oznacza, że istnieją wartości wydłużające jeden z “ogonów” rozkładu.

Spośród miar tendencji centralnej, „średnia” jest najbardziej zależna od kierunku skośności.

Jak opisać poniższy skos?
Czy uważasz, że „średnia” byłaby wyższa czy niższa niż „mediana”?

sns.histplot(data = df_gapminder, x = "gdp_cap")
plt.axvline(df_gapminder['gdp_cap'].mean(), linestyle = "dotted");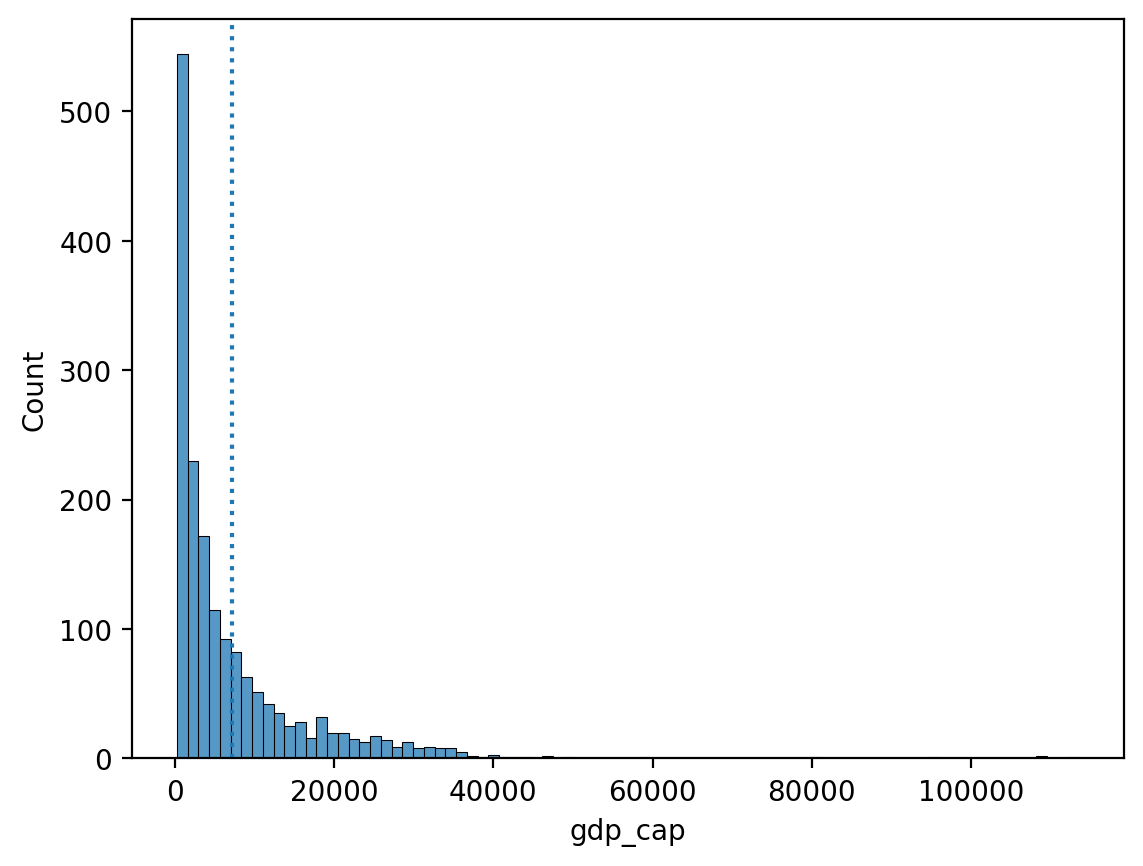

Twoja kolej¶

Czy można obliczyć średnią kolumny „kontynent”? Dlaczego lub dlaczego nie?

### Twój kod tutaj

Twoja kolej¶

Odejmij każdą obserwację w liczbach od średniej tej listy.
Następnie oblicz sumę tych odchyleń od średniej.

Jaka jest ich suma?

liczby = np.array([1, 2, 3, 4])
### Twój kod tutaj

Podsumowanie pierwszej części¶

Średnia jest jedną z najbardziej powszechnych miar tendencji centralnej.
Może być używana tylko dla ciągłych danych interwałowych/ratio.
Suma odchyleń od średniej jest równa 0.
Na „średnią” największy wpływ ma skośność i wartości odstające.

Mediana¶

Medianę oblicza się sortując wszystkie wartości od najmniejszej do największej, a następnie znajdując wartość pośrodku.

Mediana to liczba, która dzieli zbiór danych na dwie równe połowy.
Aby obliczyć medianę, musimy uporządkować nasz zbiór danych składający się z n liczb w kolejności rosnącej.
Mediana tego zbioru danych to liczba na pozycji (n+1)/2, jeśli n jest nieparzyste.
Jeśli n jest parzyste, mediana jest średnią z (n/2)trzeciej liczby i (n+2)/2 trzeciej liczby.
Mediana jest odporna na wartości odstające.
Tak więc, w przypadku rozkładu skośnego lub gdy istnieje obawa o wartości odstające, preferowana może być mediana.

df_gapminder['gdp_cap'].median()

np.float64(3531.8469885)

Porównanie `mediany` i `średniej`¶

Kierunek pochylenia ma mniejszy wpływ na medianę.

sns.histplot(data = df_gapminder, x = "gdp_cap")
plt.axvline(df_gapminder['gdp_cap'].mean(), linestyle = "dotted", color = "blue")
plt.axvline(df_gapminder['gdp_cap'].median(), linestyle = "dashed", color = "red");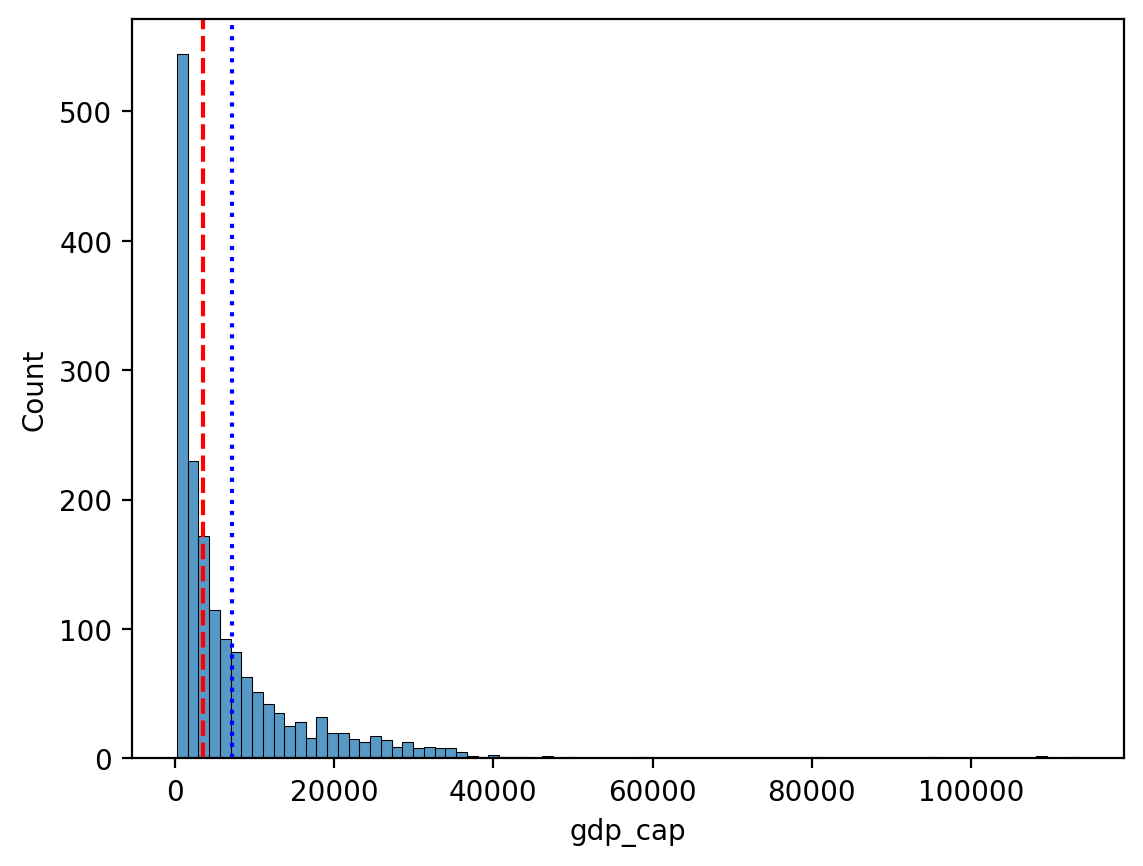

Twoja kolej¶

Czy można obliczyć medianę kolumny „kontynent”?

### Twoja odpowiedź tutaj

Moda¶

Moda jest najczęściej występującą wartością w zbiorze danych.

W przeciwieństwie do mediany lub średniej, moda może być używana z kategorycznymi danymi.

df_pokemon = pd.read_csv("data/pokemon.csv")
df_pokemon['Type 1'].mode()

0    Water
Name: Type 1, dtype: object

`mode()` zwraca wiele wartości?¶

Jeśli wiele wartości wiąże się dla najczęstszej, mode() zwróci je wszystkie.
Dzieje się tak dlatego, że technicznie rzecz biorąc, rozkład może mieć wiele wartości najczęstszych - modalnych!

df_gapminder['gdp_cap'].mode()

0          241.165876
1          277.551859
2          298.846212
3          299.850319
4          312.188423
            ...      
1699     80894.883260
1700     95458.111760
1701    108382.352900
1702    109347.867000
1703    113523.132900
Name: gdp_cap, Length: 1704, dtype: float64

Miary tendencji centralnej - podsumowanie¶

Miara	Może być użyta dla:	Ograniczenia
Średnia	Dane ciągłe	Wpływ na skośność i wartości odstające
Mediana	Dane ciągłe	Nie uwzględnia wartości wszystkich punktów danych w obliczeniach (tylko rangi)
Moda	Dane ciągłe i kategoryczne	Uwzględnia tylko najczęstsze; ignoruje inne wartości

Kwantyle¶

Kwantyle to statystyki opisowe - pozycyjne, które dzielą uporządkowany zbiór danych na równe części. Najczęściej spotykane kwantyle to:

Mediana (kwantyl rzędu 0.5),
Kwartyle (dzielą dane na 4 części),
Decyle (na 10 części),
Percentyle (na 100 części).

Definicja¶

Kwantyl rzędu $q \in (0,1)$ to taka wartość $x_q$ , że:

P(X \leq x_q) = q

(2)

Inaczej mówiąc: $q \cdot 100\%$ wartości w zbiorze danych jest mniejszych lub równych $x_q$ .

Wzór (dla uporządkowanego zbioru danych)¶

Dla próbki danych $x_1, x_2, \ldots, x_n$ uporządkowanej rosnąco, kwantyl rzędu $q$ wyznacza się jako:

Oblicz indeks pozycyjny:

i = q \cdot (n + 1)

(3)

Jeśli $i$ jest liczbą całkowitą, to kwantyl to $x_i$ .
Jeśli $i$ nie jest całkowite, interpolujemy liniowo pomiędzy sąsiednimi wartościami:

x_q = x_{\lfloor i \rfloor} + (i - \lfloor i \rfloor) \cdot (x_{\lceil i \rceil} - x_{\lfloor i \rfloor})

(4)

Uwaga: W praktyce stosuje się różne metody wyznaczania kwantyli — biblioteki takie jak NumPy czy Pandas mają różne tryby (np. method='linear', method='midpoint').

Przykład - obliczamy na piechotę¶

Dla danych:
$[3, 7, 8, 5, 12, 14, 21, 13, 18]$

Porządkujemy dane rosnąco:

$[3, 5, 7, 8, 12, 13, 14, 18, 21]$

Mediana (kwantyl rzędu 0.5):

Liczba elementów $n = 9$ , środkowy element to 5-ta wartość:

$\text{Mediana} = x_5 = 12$

Pierwszy kwartyl (Q1, kwantyl rzędu 0.25):

$i = 0.25 \cdot (9 + 1) = 2.5$

Interpolacja między $x_2 = 5$ i $x_3 = 7$ :

$Q_1 = 5 + 0.5 \cdot (7 - 5) = 6$

Trzeci kwartyl (Q3, kwantyl rzędu 0.75):

$i = 0.75 \cdot 10 = 7.5$

Interpolacja między $x_7 = 14$ i $x_8 = 18$ :

$Q_3 = 14 + 0.5 \cdot (18 - 14) = 16$

Decyle¶

Decyle dzielą dane na 10 równych części. Przykładowo:

D1 to 10-ty percentyl (kwantyl rzędu 0.1),
D5 to mediana (0.5),
D9 to 90-ty percentyl (0.9).

Wzór taki sam jak dla ogólnych kwantyli, wystarczy użyć odpowiedniego $q$ . Np. dla D3:

$q = \frac{3}{10} = 0.3$

Percentyle¶

Percentyle dzielą dane na 100 równych części. Np.:

P25 = Q1,
P50 = mediana,
P75 = Q3,
P90 to wartość, poniżej której znajduje się 90% danych.

Dzięki percentylom możemy lepiej zrozumieć rozkład danych – np. w testach standardowych często wynik podaje się jako percentyl (np. “85 percentyl” oznacza, że ktoś osiągnął wynik lepszy niż 85% populacji).

Kwantyle - podsumowanie¶

Nazwa	Symbol	Kwantyl ( q )	Znaczenie
Q1	Q1	0.25	25% danych ≤ Q1
Mediana	Q2	0.5	50% danych ≤ Mediana
Q3	Q3	0.75	75% danych ≤ Q3
Decyl 1	D1	0.1	10% danych ≤ D1
Decyl 9	D9	0.9	90% danych ≤ D9
Percentyl 95	P95	0.95	95% danych ≤ P95

Przykład - obliczamy kwantyle¶

# Dane przykładowe
dane = [3, 7, 8, 5, 12, 14, 21, 13, 18]
dane_sorted = sorted(dane)
print("Posortowane dane:", dane_sorted)

Posortowane dane: [3, 5, 7, 8, 12, 13, 14, 18, 21]

# Konwersja na obiekt Pandas Series
s = pd.Series(dane)

# Kwartyle
q1 = s.quantile(0.25)
median = s.quantile(0.5)
q3 = s.quantile(0.75)

# Decyle
d1 = s.quantile(0.1)
d9 = s.quantile(0.9)

# Percentyle
p95 = s.quantile(0.95)

print("Kwantyle:")
print(f"Q1 (25%): {q1}")
print(f"Mediana (50%): {median}")
print(f"Q3 (75%): {q3}")
print("\nDecyle:")
print(f"D1 (10%): {d1}")
print(f"D9 (90%): {d9}")
print("\nPercentyle:")
print(f"P95 (95%): {p95}")

Kwantyle:
Q1 (25%): 7.0
Mediana (50%): 12.0
Q3 (75%): 14.0

Decyle:
D1 (10%): 4.6
D9 (90%): 18.6

Percentyle:
P95 (95%): 19.799999999999997

plt.figure(figsize=(6, 4))
plt.boxplot(dane, vert=False, patch_artist=True, boxprops=dict(facecolor='lightblue'));
plt.title("Boxplot – Rozkład danych")
plt.xlabel("Wartości")
plt.grid(True, axis='x', linestyle='--', alpha=0.7)
plt.show()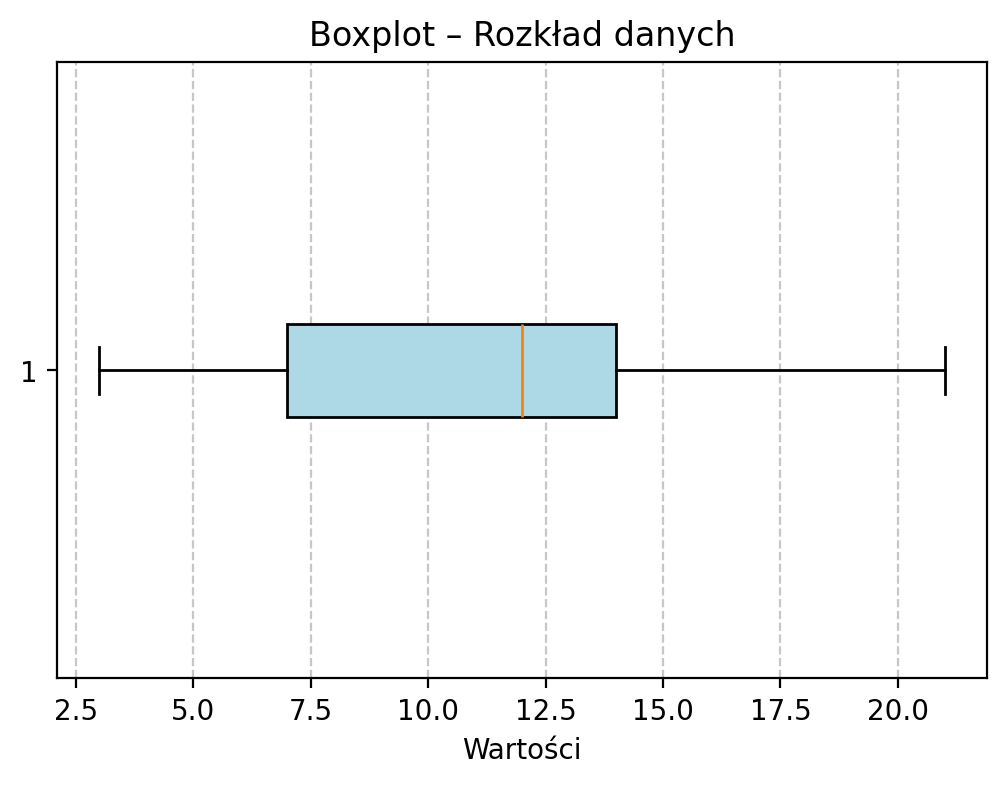

Twoja kolej!¶

Patrząc na w/w wyniki kwantyli oraz wykres pudełkowy postaraj się zinterpretować te miary.

Zmienność¶

Zmienność (lub rozproszenie) odnosi się do stopnia, w jakim wartości w rozkładzie są rozproszone, tj. różnią się od siebie.

Rozproszenie jest wskaźnikiem tego, jak daleko od środka możemy znaleźć wartości danych. Najpopularniejszymi miarami rozproszenia są wariancja, odchylenie standardowe i rozstęp międzykwartylowy (IQR). Wariancja jest standardową miarą rozrzutu. Odchylenie standardowe jest pierwiastkiem kwadratowym z wariancji. Wariancja i odchylenie standardowe to dwie użyteczne miary rozrzutu.

`średnia` ukrywa wariancję¶

Oba rozkłady mają tę samą średnią, ale różne odchylenia standardowe.

### Tworzymy rozkłady
d1 = np.random.normal(loc = 0, scale = 1, size = 1000)
d2 = np.random.normal(loc = 0, scale = 5, size = 1000)
### Wykresy
fig, axes = plt.subplots(1, 2, sharex=True, sharey=True);
p1 = axes[0].hist(d1, alpha = .5)
p2 = axes[1].hist(d2, alpha = .5)
axes[0].set_title("Niższa wariancja");
axes[1].set_title("Wyższa wariancja");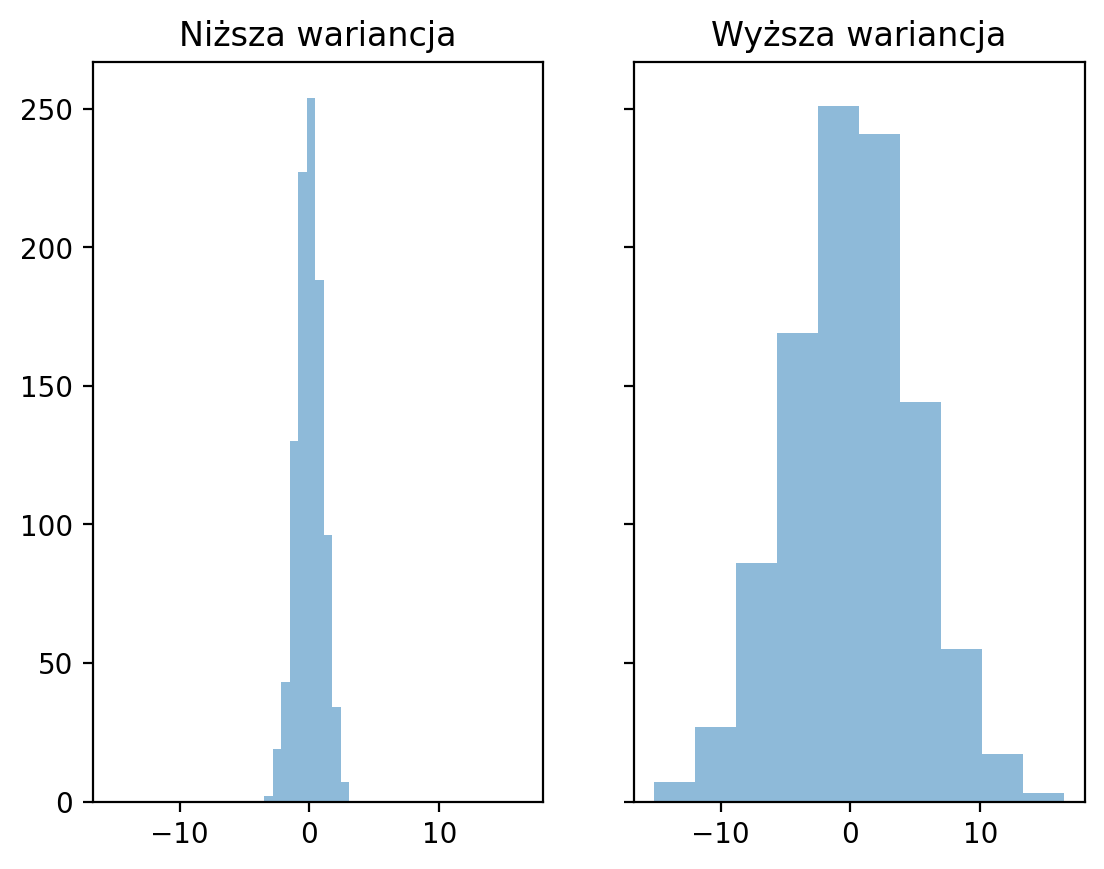

Wykrywanie zmienności¶

Istnieją co najmniej trzy główne podejścia do kwantyfikacji zmienności:

Zakres: różnica między wartością „maksymalną” i „minimalną”.
Zakres międzykwartylowy (IQR): Zakres środkowych 50% danych.
Wariancja i Odchylenie standardowe: typowa wartość, o jaką wyniki odbiegają od średniej.

Rozstęp¶

Rozstęp jest różnicą pomiędzy wartością maksymalną i minimalną.

Intuicyjne, ale uwzględnia tylko dwie wartości w całej dystrybucji.

d1.max() - d1.min()

np.float64(6.580628568373348)

d2.max() - d2.min()

np.float64(31.571899756007486)

IQR¶

Rozstęp międzykwartylowy (IQR) to różnica między wartością w 75% percentylu a wartością w 25% percentylu.

Koncentruje się na środkowych 50%, ale nadal uwzględnia tylko dwie wartości.

IQR jest obliczany przy użyciu granic danych znajdujących się między 1. a 3. kwartylem.
Przedział międzykwartylowy (IQR) można obliczyć w następujący sposób: $IQR = Q3 - Q1$
W ten sam sposób, w jaki mediana jest bardziej odporna niż średnia, IQR jest bardziej odporną miarą rozrzutu niż wariancja i odchylenie standardowe i dlatego powinien być preferowany w przypadku małych lub asymetrycznych rozkładów.
Jest to solidna miara rozrzutu.

## Obliczamy kwantyle - kwartyle Q1 oraz Q3
q3, q1 = np.percentile(d1, [75 ,25])
q3 - q1

np.float64(1.3316655702366968)

## Obliczamy kwantyle - kwartyle Q1 oraz Q3
q3, q1 = np.percentile(d2, [75 ,25])
q3 - q1

np.float64(6.309359612149275)

Wariancja i odchylenie standardowe¶

Wariancja mierzy rozproszenie zestawu punktów danych wokół ich średniej wartości. Jest to średnia kwadratów poszczególnych odchyleń. Wariancja daje wyniki w oryginalnych jednostkach podniesionych do kwadratu.

s^2 = \frac{1}{n - 1} \sum_{i=1}^{n} (x_i - \bar{x})^2

(5)

Odchylenie standardowe (SD) mierzy typową wartość, o jaką wyniki w rozkładzie odbiegają od średniej.

s = \sqrt{s^2} = \sqrt{\frac{1}{n - 1} \sum_{i=1}^{n} (x_i - \bar{x})^2}

(6)

gdzie: • $n$ – liczba elementów w próbie • $\bar{x}$ – średnia arytmetyczna próby

O czym należy pamiętać:

SD jest pierwiastkiem kwadratowym z wariancji.
W rzeczywistości istnieją dwie miary SD:
SD populacji: gdy mierzysz całą populację zainteresowania (bardzo rzadko).
- SD próbki: gdy mierzysz próbkę (typowy przypadek); skupimy się na tym.

SD, objaśnione¶

Najpierw oblicz sumę odchyleń kwadratowych.
- Jakie jest całkowite odchylenie kwadratowe od „średniej”?
Następnie podziel przez n - 1: znormalizuj do liczby obserwacji.
- Ile wynosi średnie kwadratowe odchylenie od „średniej”?
Na koniec weź pierwiastek kwadratowy:
- Jakie jest średnie odchylenie od „średniej”?

Odchylenie standardowe reprezentuje typowe lub „średnie” odchylenie od „średniej”.

Obliczanie SD w `pandas`¶

df_pokemon['Attack'].std()

np.float64(32.45736586949845)

df_pokemon['HP'].std()

np.float64(25.53466903233207)

Uwaga na `np.std`¶

Domyślnie, numpy.std oblicza odchylenie standardowe populacji!
Należy zmodyfikować parametr ddof, aby obliczyć próbkowe odchylenie standardowe.

Jest to bardzo częsty błąd.

### SD populacji
d1.std()

np.float64(1.012275006518212)

### SD próby
d1.std(ddof = 1)

np.float64(1.0127815239412115)

Współczynnik zmienności (CV)¶

Współczynnik zmienności (CV) jest równy odchyleniu standardowemu podzielonemu przez średnią.
Jest również znany jako „względne odchylenie standardowe”.

CV = \frac{s}{\bar{x}} \cdot 100%

(7)

X = [2, 4, 4, 4, 5, 5, 7, 9]
mean = np.mean(X)

# Wariancja i odchylenie standardowe z scipy (dla próby!)
var_sample = stats.tvar(X)      # wariancja próby
std_sample = stats.tstd(X)      # odchylenie standardowe próby

# Współczynnik zmienności (dla próby)
cv_sample = (std_sample / mean) * 100

print(f"Średnia: {mean}")
print(f"Wariancja próby (scipy): {var_sample}")
print(f"Odchylenie standardowe próby (scipy): {std_sample}")
print(f"Współczynnik zmienności (scipy): {cv_sample:.2f}%")

Średnia: 5.0
Wariancja próby (scipy): 4.571428571428571
Odchylenie standardowe próby (scipy): 2.138089935299395
Współczynnik zmienności (scipy): 42.76%

Odchylenie międzykwartylowe¶

Odchylenie międzykwartylowe (czasami nazywane zakresem półinterkwartylowym) jest definiowane jako połowa zakresu międzykwartylowego:

\text{Odchylenie IQR} = \frac{Q3 - Q1}{2}

(8)

Wartość ta pokazuje średnią odległość od mediany do kwartyli i jest solidną miarą zmienności.

Małe odchylenie międzykwartylowe oznacza, że środkowe 50% danych znajduje się blisko mediany.
Duże odchylenie międzykwartylowe oznacza, że środkowe 50% danych jest bardziej rozproszone.

Jest ono mniej wrażliwe na wartości odstające niż odchylenie standardowe lub zakres!

Twoja kolej!¶

Oblicz STD i CV dla prędkości (Speed) pokemonów legendarnych i nie-legendarnych. Jakie jest odchylenie IQR?

# Twój kod tutaj!

# %load ./solutions/solution8.py

Miary kształtu rozkładu¶

Teraz przyjrzymy się miarom kształtu rozkładu. Istnieją dwie miary statystyczne, które mogą nam powiedzieć o kształcie rozkładu. Są to skośność i kurtoza. Miary te mogą być wykorzystane do przekazania informacji o kształcie rozkładu zbioru danych.

Skośność¶

Skośność jest miarą symetrii rozkładu, a dokładniej jej braku.
Jest używana do określenia braku symetrii względem średniej zbioru danych.
Jest to charakterystyka odchylenia od średniej.
Służy do wskazania kształtu rozkładu danych.

Skośność to miara asymetrii rozkładu danych względem średniej. Mówi nam, czy dane są bardziej „rozciągnięte” w jedną ze stron.

Interpretacja:

Skośność > 0 – prawostronna (dodatnia): długi ogon z prawej strony (większe wartości są bardziej rozproszone)
Skośność < 0 – lewostronna (ujemna): długi ogon z lewej strony (mniejsze wartości są bardziej rozproszone)
Skośność ≈ 0 – rozkład symetryczny (np. rozkład normalny)

Wzór (dla próby):

A = \frac{n}{(n-1)(n-2)} \sum_{i=1}^{n} \left( \frac{x_i - \bar{x}}{s} \right)^3

(9)

gdzie: • $n$ – liczba obserwacji • $\bar{x}$ – średnia próby • $s$ – odchylenie standardowe próby

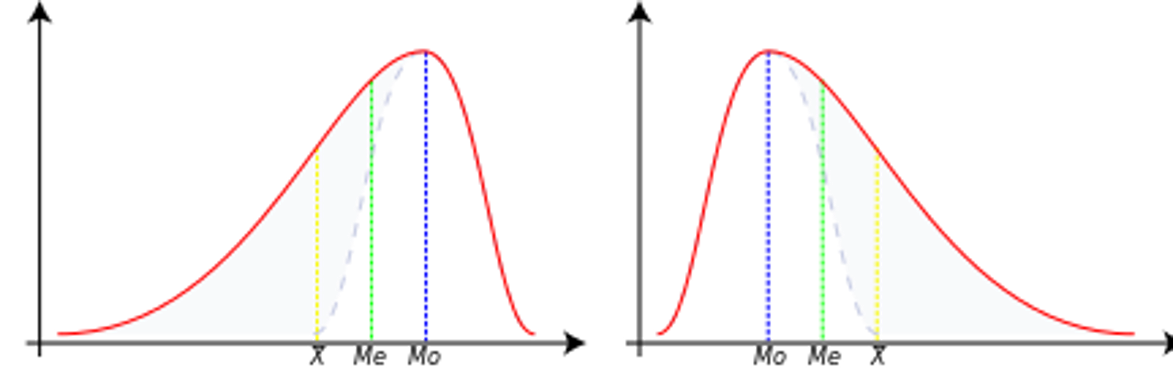
Ujemna skośność¶

W tym przypadku dane są przekrzywione lub przesunięte w lewo.
Przez przekrzywienie w lewo rozumiemy, że lewy ogon jest długi w stosunku do prawego ogona.
Wartości danych mogą rozciągać się dalej w lewo, ale koncentrują się po prawej stronie.
Mamy więc do czynienia z długim ogonem, a zniekształcenia są powodowane przez bardzo małe wartości, które ciągną średnią w dół i jest ona mniejsza niż mediana.
W tym przypadku mamy Średnia < Mediana < Moda

Zerowa skośność¶

Oznacza to, że zbiór danych jest symetryczny.
Zbiór danych jest symetryczny, jeśli wygląda tak samo po lewej i prawej stronie punktu środkowego.
Zbiór danych ma kształt dzwonu lub jest symetryczny.
Idealnie symetryczny zestaw danych będzie miał skośność równą zero.
Tak więc rozkład normalny, który jest idealnie symetryczny, ma skośność równą 0.
W tym przypadku mamy Średnia = Mediana = Moda

Dodatnia skośność¶

Zbiór danych jest przekrzywiony lub przesunięty w prawo.
Przez przekrzywienie w prawo rozumiemy, że prawy ogon jest długi w stosunku do lewego ogona.
Wartości danych są skoncentrowane po prawej stronie.
Istnieje długi ogon po prawej stronie, który jest spowodowany bardzo dużymi wartościami, które podciągają średnią w górę i jest ona większa niż mediana.
Mamy więc Średnia > Mediana > Moda

X = [2, 4, 4, 4, 5, 5, 7, 9]

# Obliczanie skośności
skewness = stats.skew(X)
print(f"Skośność zbioru danych: {skewness:.4f}")

Skośność zbioru danych: 0.6562

Twoja kolej¶

Postaraj się zinterpretować w/w wynik oraz obliczyć przykładowe wskaźniki skośności dla obu grup pokemonów Legendarnych i Nie-legendarnych - dla zmiennej Speed.

# Twój kod tutaj

Skośność międzykwartylowa¶

Skośność IQR jest solidną, nieparametryczną miarą skośności, która wykorzystuje pozycje kwartyli zamiast średniej i odchylenia standardowego. Jest ona szczególnie przydatna do wykrywania asymetrii w rozkładach danych, zwłaszcza w przypadku występowania wartości odstających.

Wzór na skośność IQR to:

IQR\ Skośność = \frac{(Q3 - Mediana) - (Mediana - Q1)}{Q3 - Q1}

(10)

Metoda ta jest mniej wrażliwa na wartości odstające i bardziej solidna niż skośność oparta na momentach, co czyni ją idealną do analizy danych eksploracyjnych.

Twoja kolej!¶

Spróbuj obliczyć współczynnik skośności IQR dla punktów za prędkość (Speed) dla obu typów (legendarne i nie-legendarne) pokemonów.

# Twój kod tutaj!

# %load ./solutions/solution9.py
# Skośność IQR dla punktów za atak (Attack) dla kilku generacji pokemonów

Kurtoza¶

W przeciwieństwie do tego, co podają niektóre podręczniki, kurtoza nie mierzy „spłaszczenia”, „szczytowości” rozkładu.

Kurtoza zależy od intensywności skrajnych wartości, więc mierzy to, co dzieje się w „ogonach” rozkładu, kształt „wierzchołka” nie ma żadnego znaczenia!

Kurtoza próby:

\text{Kurtoza} = \frac{1}{n} \sum_{i=1}^{n} \left( \frac{x_i - \bar{x}}{s} \right)^4

(11)

\text{Kurtoza znormalizowana} = \text{Kurtoza} - 3

(12)

Zakres referencyjny dla kurtozy¶

Standardem referencyjnym jest rozkład normalny, który ma kurtozę równą 3.
Często zamiast kurtozy prezentowana jest eksces, gdzie eksces to po prostu kurtoza - 3.

Krzywa mezokurtyczna¶

Rozkład normalny ma kurtozę dokładnie 3 (eksces dokładnie 0).
Każdy rozkład z kurtozą ≈3 (eksces ≈ 0) nazywany jest mezokurtycznym.

Krzywa platykurtyczna¶

Rozkład z kurtozą < 3 (eksces < 0) nazywany jest platykurtycznym.
W porównaniu do rozkładu normalnego, jego centralny szczyt jest niższy i szerszy, a jego ogony są krótsze i cieńsze.

Krzywa leptokurtyczna¶

Rozkład z kurtozą > 3 (eksces > 0) nazywany jest leptokurtycznym.
W porównaniu do rozkładu normalnego, jego centralny szczyt jest wyższy i ostrzejszy, a jego ogony są dłuższe i grubsze.

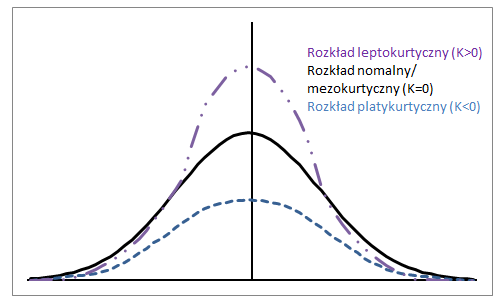
from scipy.stats import kurtosis
dane = [2, 4, 4, 4, 5, 5, 7, 9]
# Obliczanie kurtozy (domyślnie znormalizowana, czyli -3 już odjęte)
kurtoza_znormalizowana = kurtosis(dane)
# Jeśli chcesz surową (bez odejmowania 3), ustaw fisher=False
kurtoza_surowa = kurtosis(dane, fisher=False)
print("Kurtoza znormalizowana:", kurtoza_znormalizowana)
print("Kurtoza surowa:", kurtoza_surowa)

Kurtoza znormalizowana: -0.21875
Kurtoza surowa: 2.78125

Kurtoza międzykwartylowa¶

IQR Kurtoza to solidna, nieparametryczna miara kurtozy, która koncentruje się na ogonach rozkładu przy użyciu przedziałów międzykwartylowych. Jest szczególnie przydatna do wykrywania intensywności wartości ekstremalnych w rozkładach danych, zwłaszcza gdy występują wartości odstające.

Wzór na kurtozę IQR to:

IQR\ Kurtoza = \frac{Q3 - Q1}{2*(C90 - C10)}

(13)

Gdzie:

$Q1$ to pierwszy kwartyl (25 percentyl),
$Q3$ to trzeci kwartyl (75. percentyl),
$C90$ to 90. percentyl,
$C10$ to 10. percentyl.

Interpretacja:

Kurtoza IQR różni się od tradycyjnej kurtozy pod względem interpretacji. Podczas gdy tradycyjna kurtoza koncentruje się na intensywności ogonów rozkładu (np. ciężkie lub lekkie ogony), kurtoza IQR jest solidną miarą, która podkreśla względny rozrzut przedziału międzykwartylowego (IQR) i symetrię rozkładu wokół mediany.

Twoja kolej!¶

Spróbuj obliczyć współczynnik kurtozy IQR dla ataku legendarnych pokemonów.

# Twój kod tutaj!

# %load ./solutions/solution10.py
# Kurtoza IQR dla ataku (Attack) legendarnych pokemonów
from scipy.stats import kurtosis
legendary_attack = df_pokemon[df_pokemon['Legendary'] == True]['Attack']

q1 = legendary_attack.quantile(0.25)
q3 = legendary_attack.quantile(0.75)
c10 = legendary_attack.quantile(0.10)
c90 = legendary_attack.quantile(0.90)

iqr_kurtoza = (q3 - q1) / (2 * (c90 - c10))
kurtoza = kurtosis(legendary_attack)
print(f"Kurtoza klasyczna dla ataku legendarnych pokemonów: {kurtoza:.3f}")
print(f"Kurtoza IQR dla ataku legendarnych pokemonów: {iqr_kurtoza:.3f}")

Kurtoza klasyczna dla ataku legendarnych pokemonów: -0.266
Kurtoza IQR dla ataku legendarnych pokemonów: 0.207

Podsumowanie statystyk¶

Świetnym narzędziem do tworzenia eleganckich podsumowań statystyk opisowych w formacie markdown (idealnym do Jupyter Notebooków) jest pandas, szczególnie w połączeniu z funkcją .describe() oraz tabulate.

Przykład z pandas + tabulate (ładna tabela w Markdown):

from scipy.stats import skew, kurtosis
from tabulate import tabulate

def markdown_summary(df, round_decimals=3):
    summary = df.describe().T  # transponujemy, żeby zmienne były w wierszach
    # Dodajemy skośność i kurtozę
    summary['skośność'] = df.skew()
    summary['kurtoza'] = df.kurt()
    # Zaokrąglenie wyników
    summary = summary.round(round_decimals)
    # Tabelka z wynikami!
    return tabulate(summary, headers='keys', tablefmt='github')

# Wybieramy tylko kolumny numeryczne do analizy
ilosciowe = df_pokemon.select_dtypes(include='number')

# Używamy naszej funkcji
print(markdown_summary(ilosciowe))

|            |   count |    mean |     std |   min |    25% |   50% |    75% |   max |   skośność |   kurtoza |
|------------|---------|---------|---------|-------|--------|-------|--------|-------|------------|-----------|
| #          |     800 | 362.814 | 208.344 |     1 | 184.75 | 364.5 | 539.25 |   721 |     -0.001 |    -1.166 |
| Total      |     800 | 435.102 | 119.963 |   180 | 330    | 450   | 515    |   780 |      0.153 |    -0.507 |
| HP         |     800 |  69.259 |  25.535 |     1 |  50    |  65   |  80    |   255 |      1.568 |     7.232 |
| Attack     |     800 |  79.001 |  32.457 |     5 |  55    |  75   | 100    |   190 |      0.552 |     0.17  |
| Defense    |     800 |  73.842 |  31.184 |     5 |  50    |  70   |  90    |   230 |      1.156 |     2.726 |
| Sp. Atk    |     800 |  72.82  |  32.722 |    10 |  49.75 |  65   |  95    |   194 |      0.745 |     0.298 |
| Sp. Def    |     800 |  71.902 |  27.829 |    20 |  50    |  70   |  90    |   230 |      0.854 |     1.628 |
| Speed      |     800 |  68.278 |  29.06  |     5 |  45    |  65   |  90    |   180 |      0.358 |    -0.236 |
| Generation |     800 |   3.324 |   1.661 |     1 |   2    |   3   |   5    |     6 |      0.014 |    -1.24  |

Aby zrobić tabelkę podsumowującą przekrojowo (czyli w podziale na grupy), trzeba skorzystać z metody groupby() na DataFrame, a potem np. describe() lub własnej funkcji agregującej.

Załóżmy, że chcesz pogrupować dane według kolumny “Type 1” (czyli np. typ pokémona: Fire, Water itd.), a potem podsumować zmienne ilościowe (średnia, odchylenie, min, max itd.).

# Grupowanie po kolumnie 'Type 1' i podsumowanie statystyczne kolumn numerycznych
grupowe_podsumowanie = df_pokemon.groupby('Type 1')[ilosciowe.columns].describe()
print(grupowe_podsumowanie)

              #                                                               \
          count        mean         std    min     25%    50%     75%    max   
Type 1                                                                         
Bug        69.0  334.492754  210.445160   10.0  168.00  291.0  543.00  666.0   
Dark       31.0  461.354839  176.022072  197.0  282.00  509.0  627.00  717.0   
Dragon     32.0  474.375000  170.190169  147.0  373.00  443.5  643.25  718.0   
Electric   44.0  363.500000  202.731063   25.0  179.75  403.5  489.75  702.0   
Fairy      17.0  449.529412  271.983942   35.0  176.00  669.0  683.00  716.0   
Fighting   27.0  363.851852  218.565200   56.0  171.50  308.0  536.00  701.0   
Fire       52.0  327.403846  226.262840    4.0  143.50  289.5  513.25  721.0   
Flying      4.0  677.750000   42.437209  641.0  641.00  677.5  714.25  715.0   
Ghost      32.0  486.500000  209.189218   92.0  354.75  487.0  709.25  711.0   
Grass      70.0  344.871429  200.264385    1.0  187.25  372.0  496.75  673.0   
Ground     32.0  356.281250  204.899855   27.0  183.25  363.5  535.25  645.0   
Ice        24.0  423.541667  175.465834  124.0  330.25  371.5  583.25  713.0   
Normal     98.0  319.173469  193.854820   16.0  161.25  296.5  483.00  676.0   
Poison     28.0  251.785714  228.801767   23.0   33.75  139.5  451.25  691.0   
Psychic    57.0  380.807018  194.600455   63.0  201.00  386.0  528.00  720.0   
Rock       44.0  392.727273  213.746140   74.0  230.75  362.5  566.25  719.0   
Steel      27.0  442.851852  164.847180  208.0  305.50  379.0  600.50  707.0   
Water     112.0  303.089286  188.440807    7.0  130.00  275.0  456.25  693.0   

          Total              ...   Speed        Generation            \
          count        mean  ...     75%    max      count      mean   
Type 1                       ...                                       
Bug        69.0  378.927536  ...   85.00  160.0       69.0  3.217391   
Dark       31.0  445.741935  ...   98.50  125.0       31.0  4.032258   
Dragon     32.0  550.531250  ...   97.75  120.0       32.0  3.875000   
Electric   44.0  443.409091  ...  101.50  140.0       44.0  3.272727   
Fairy      17.0  413.176471  ...   60.00   99.0       17.0  4.117647   
Fighting   27.0  416.444444  ...   86.00  118.0       27.0  3.370370   
Fire       52.0  458.076923  ...   96.25  126.0       52.0  3.211538   
Flying      4.0  485.000000  ...  121.50  123.0        4.0  5.500000   
Ghost      32.0  439.562500  ...   84.25  130.0       32.0  4.187500   
Grass      70.0  421.142857  ...   80.00  145.0       70.0  3.357143   
Ground     32.0  437.500000  ...   90.00  120.0       32.0  3.156250   
Ice        24.0  433.458333  ...   80.00  110.0       24.0  3.541667   
Normal     98.0  401.683673  ...   90.75  135.0       98.0  3.051020   
Poison     28.0  399.142857  ...   77.00  130.0       28.0  2.535714   
Psychic    57.0  475.947368  ...  104.00  180.0       57.0  3.385965   
Rock       44.0  453.750000  ...   70.00  150.0       44.0  3.454545   
Steel      27.0  487.703704  ...   70.00  110.0       27.0  3.851852   
Water     112.0  430.455357  ...   82.00  122.0      112.0  2.857143   

                                               
               std  min   25%  50%   75%  max  
Type 1                                         
Bug       1.598433  1.0  2.00  3.0  5.00  6.0  
Dark      1.353609  2.0  3.00  5.0  5.00  6.0  
Dragon    1.431219  1.0  3.00  4.0  5.00  6.0  
Electric  1.604697  1.0  2.00  4.0  4.25  6.0  
Fairy     2.147160  1.0  2.00  6.0  6.00  6.0  
Fighting  1.800601  1.0  1.50  3.0  5.00  6.0  
Fire      1.850665  1.0  1.00  3.0  5.00  6.0  
Flying    0.577350  5.0  5.00  5.5  6.00  6.0  
Ghost     1.693203  1.0  3.00  4.0  6.00  6.0  
Grass     1.579173  1.0  2.00  3.5  5.00  6.0  
Ground    1.588454  1.0  1.75  3.0  5.00  5.0  
Ice       1.473805  1.0  2.75  3.0  5.00  6.0  
Normal    1.575407  1.0  2.00  3.0  4.00  6.0  
Poison    1.752927  1.0  1.00  1.5  4.00  6.0  
Psychic   1.644845  1.0  2.00  3.0  5.00  6.0  
Rock      1.848375  1.0  2.00  3.0  5.00  6.0  
Steel     1.350319  2.0  3.00  3.0  5.00  6.0  
Water     1.558800  1.0  1.00  3.0  4.00  6.0  

[18 rows x 64 columns]

Analiza przekrojowa¶

Spróbujmy obliczyć wszystkie te statystyki według grup, tj. przeprowadźmy analizę opisową dla punktów ataku według legendarności (dla legendarnych i nie legendarnych pokemonów).

grouped_attack = df_pokemon.groupby('Legendary')['Attack']
grouped_summary = grouped_attack.describe()
# dodajmy skośność i kurtozę:
grouped_summary['Skośność'] = grouped_attack.apply(lambda x: x.skew())
grouped_summary['Kurtoza'] = grouped_attack.apply(lambda x: x.kurt())
from tabulate import tabulate
print(tabulate(grouped_summary, headers='keys', tablefmt='github'))

| Legendary   |   count |     mean |     std |   min |   25% |   50% |   75% |   max |   Skośność |   Kurtoza |
|-------------|---------|----------|---------|-------|-------|-------|-------|-------|------------|-----------|
| False       |     735 |  75.6694 | 30.4902 |     5 |  54.5 |    72 |    95 |   185 |   0.523333 |  0.145037 |
| True        |      65 | 116.677  | 30.348  |    50 | 100   |   110 |   131 |   190 |   0.50957  | -0.18957  |

Analiza korelacji¶

Do tej pory skupialiśmy się na jednostkowych danych: pojedynczym rozkładzie.
A co jeśli chcemy opisać, jak dwa rozkłady odnoszące się do siebie nawzajem?

Korelacje ilościowe¶

Zależności liniowe: `wysokość`¶

Klasycznym przykładem ciągłych danych jest wysokość rodzica i dziecka.
Dane te zostały zebrane przez Karla Pearsona](https://www.kaggle.com/datasets/abhilash04/fathersandsonheight).

df_height = pd.read_csv("data/wrangling/height.csv")
df_height.head(2)

Wykreślanie danych Pearsona dotyczących wysokości¶

sns.scatterplot(data = df_height, x = "Father", y = "Son", alpha = .5);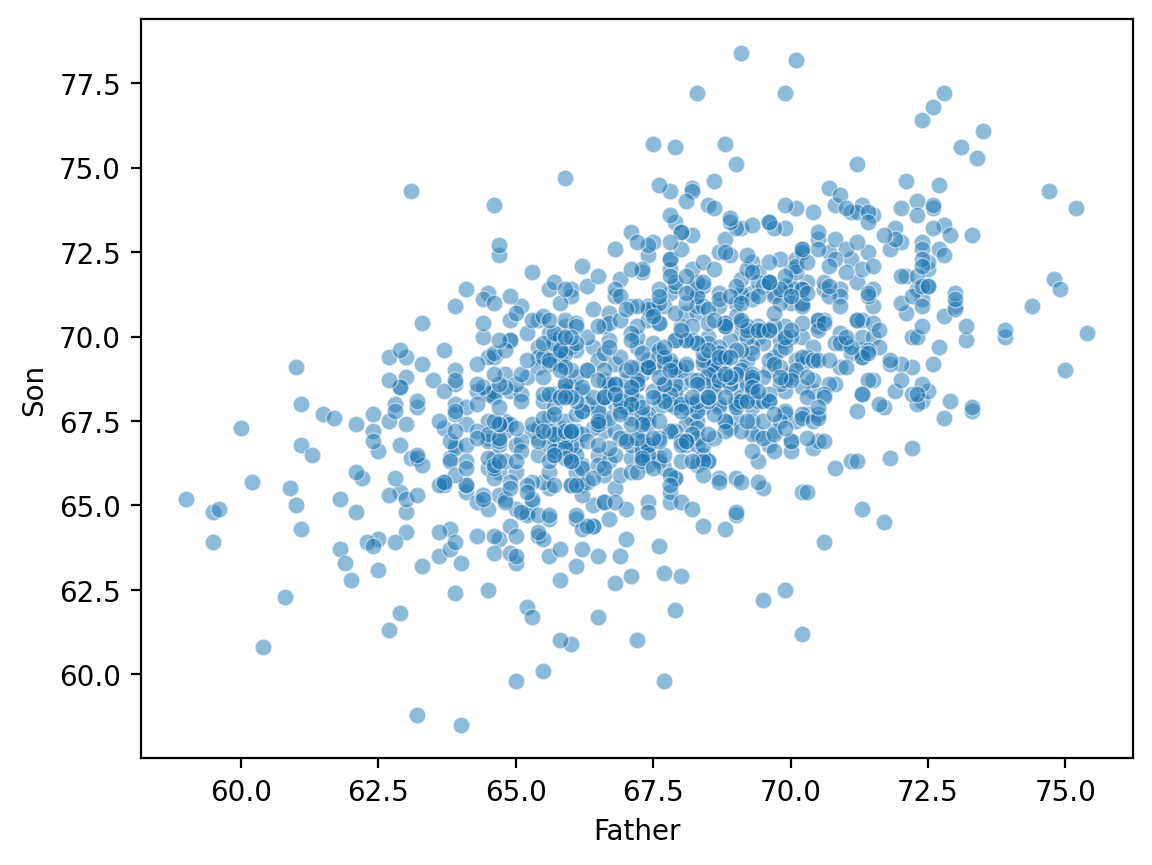

Wprowadzenie do korelacji liniowych¶

Współczynnik korelacji jest liczbą z przedziału $[-1, 1]$ , która opisuje związek pomiędzy parą zmiennych.

W szczególności, współczynnik korelacji Pearsona (lub $r$ Pearsona) opisuje (domniemaną) liniową zależność.

Dwie kluczowe właściwości:

Znak: czy związek jest dodatni (+) czy ujemny (-).
Wielkość: siła związku liniowego.

r = \frac{ \sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y}) }{ \sqrt{ \sum_{i=1}^{n} (x_i - \bar{x})^2 } \sqrt{ \sum_{i=1}^{n} (y_i - \bar{y})^2 } }

(14)

Gdzie:

$r$ – współczynnik korelacji Pearsona
$x_i$ , $y_i$ – wartości zmiennych
$\bar{x}$ , $\bar{y}$ – średnie arytmetyczne
$n$ – liczba obserwacji

Współczynnik korelacji Pearsona mierzy siłę i kierunek liniowej zależności między dwiema zmiennymi ciągłymi. Jego wartość zawiera się w przedziale od –1 do 1:

1 → idealna dodatnia korelacja liniowa
0 → brak korelacji liniowej
–1 → idealna ujemna korelacja liniowa

Współczynnik ten nie mówi o zależnościach nieliniowych i jest wrażliwy na wartości odstające.

ss.pearsonr(df_height['Father'], df_height['Son'])

PearsonRResult(statistic=np.float64(0.5011626808075912), pvalue=np.float64(1.2729275743661585e-69))

Twoja kolej¶

Używając scipy.stats.pearsonr (tutaj ss.pearsonr), oblicz $r$ Pearsona dla związku między Attack i Defense Pokemonów.

Czy związek ten jest pozytywny czy negatywny?
Jak silny jest ten związek?

### Twój kod tutaj

Ograniczenia $r$ Pearsona¶

$r$ Pearsona zakłada liniową zależność i próbuje ilościowo określić jej siłę i kierunek.
Jednak wiele zależności jest nieliniowych!
Jeśli nie wizualizujemy naszych danych, poleganie wyłącznie na $r$ Pearsona może wprowadzić nas w błąd.

Nieliniowe dane z $r = 0$ ¶

x = np.arange(1, 40)
y = np.sin(x)
p = sns.lineplot(x = x, y = y);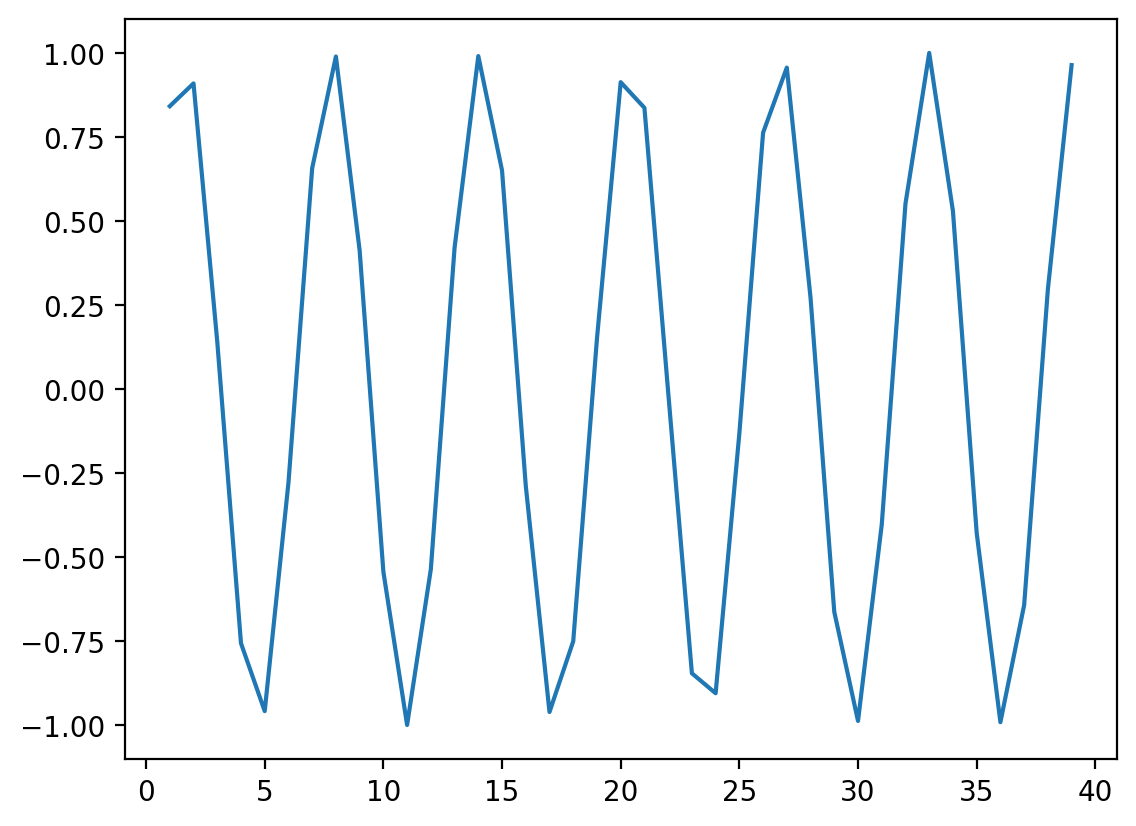

### r jest równe 0 mimo, ze widać zalezności!
ss.pearsonr(x, y)

PearsonRResult(statistic=np.float64(-0.04067793461845847), pvalue=np.float64(0.8057827185936635))

Gdy $r$ jest niezmienny względem rzeczywistej relacji¶

Wszystkie te zbiory danych mają w przybliżeniu ten sam współczynnik korelacji.

df_anscombe = sns.load_dataset("anscombe")
sns.relplot(data = df_anscombe, x = "x", y = "y", col = "dataset");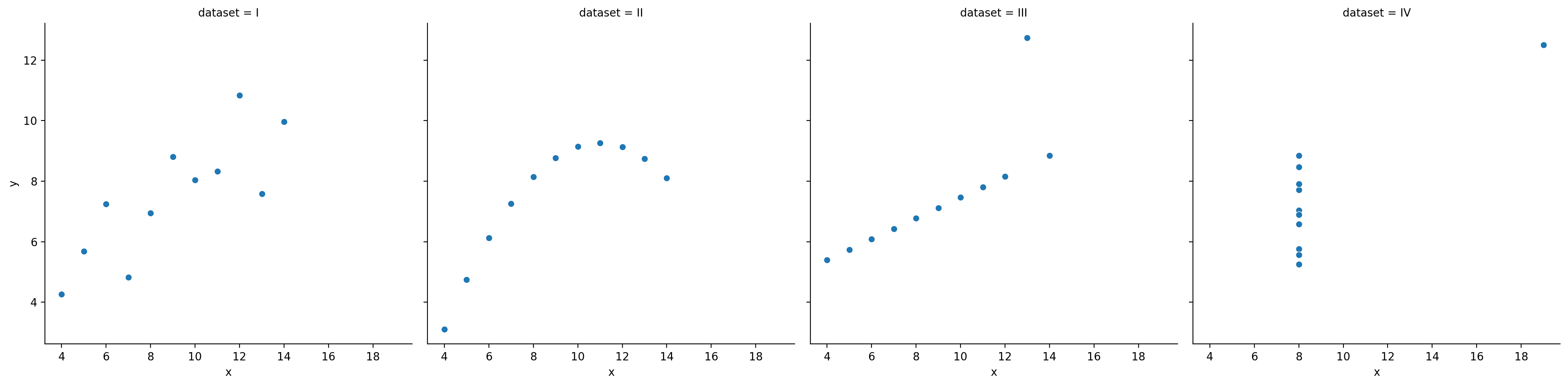

Heatmapa¶

# Oblicz macierz korelacji
corr = df_pokemon.corr(numeric_only=True)
plt.figure(figsize=(10, 8))

# rysujemy macierz korelacji - heatmapę:
sns.heatmap(corr, 
 annot=True, # pokazuj współczynniki
 fmt=".2f", # sformatuj je
 cmap="coolwarm", # paleta kolorów
 vmin=-1, vmax=1, # stała skala
 square=True, # kwadratowe komórki
 linewidths=0.5, 
 cbar_kws={"shrink": .75})  

# Tytuł i układ
plt.title("Macierz korelacji liniowych", fontsize=16)
plt.tight_layout()

# Pokaż wykres
plt.show()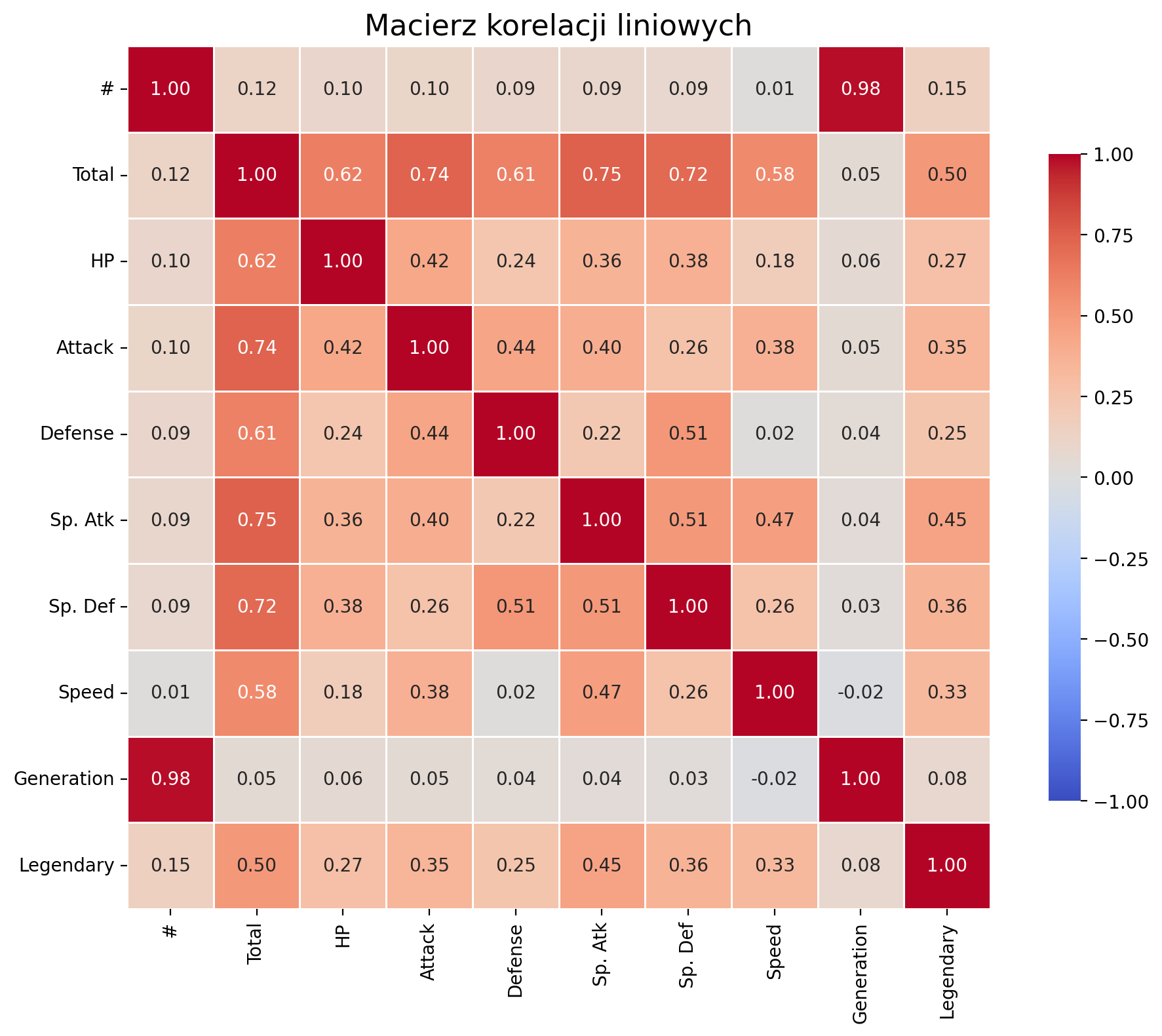

Twoja kolej¶

Postaraj się na danych Pokemonów obliczyć zalezność między Atakiem i Obroną. Zwizualizuj zalezność na wykresie rozrzutu.

## Twój kod tutaj

Korelacje rangowe¶

Korelacje rangowe to miary siły i kierunku monotonicznego (rosnącego lub malejącego) związku między dwiema zmiennymi. Zamiast wartości liczbowych wykorzystują rangi, czyli pozycje w uporządkowanym zbiorze.

Są mniej wrażliwe na wartości odstające i nie wymagają liniowości (tak jak korelacja Pearsona).

Typy korelacji rangowych¶

$ρ$ (rho) Spearmana

Opiera się na rangach danych.
Wartość: od –1 do 1
Dobrze działa dla danych związków monotonicznych, ale nieliniowych.

\rho = 1 - \frac{6 \sum d_i^2}{n(n^2 - 1)}

(15)

Gdzie:

$d_i$ – różnice rang pomiędzy obserwacjami,
$n$ – liczba obserwacji.

$τ$ (tau) Kendall’a

Mierzy liczbę par uporządkowanych zgodnie vs. przeciwnie.
Bardziej konserwatywna niż Spearman – częściej daje mniejsze wartości.
Również od –1 do 1.

\tau = \frac{(C - D)}{\frac{1}{2}n(n - 1)}

(16)

Gdzie:

$τ$ — współczynnik korelacji Kendalla,
$C$ — liczba par zgodnych (concordant pairs),
$D$ — liczba par niezgodnych (discordant pairs),
$n$ — liczba obserwacji,
$\frac{1}{2}n(n - 1)$ — liczba wszystkich możliwych par obserwacji.

Co to są pary zgodne i niezgodne?

Para zgodna (concordant): jeśli $x_i$ < $x_j$ i $y_i$ < $y_j$ , lub $x_i$ > $x_j$ i $y_i$ > $y_j$
Para niezgodna (discordant): jeśli $x_i$ < $x_j$ i $y_i$ > $y_j$ , lub $x_i$ > $x_j$ i $y_i$ < $y_j$

Kiedy stosować korelacje rangowe?¶

Gdy dane nie są normalnie rozłożone.
Gdy podejrzewasz zależność nieliniową, ale monotoniczną.
Gdy masz rangi, np. oceny, miejsce w rankingu, poziom preferencji.

Rodzaj korelacji	Opis	Kiedy stosować
Spearmana (ρ)	Zależność monotoniczna, oparta na rangach	Gdy dane są nieliniowe lub mają odstające
Kendalla (τ)	Liczy proporcje par zgodnych i niezgodnych	Gdy ważna jest odporność na wiązania - remisy rang

Interpretacja wartości korelacji¶

Zakres wartości	Interpretacja korelacji
0.8 – 1.0	bardzo silna dodatnia
0.6 – 0.8	silna dodatnia
0.4 – 0.6	umiarkowana dodatnia
0.2 – 0.4	słaba dodatnia
0.0 – 0.2	bardzo słaba lub brak korelacji
< 0	analogicznie – korelacja ujemna

Porównanie współczynników korelacji¶

Właściwość	Pearson (r)	Spearman (ρ)	Kendall (τ)
Co mierzy?	Związek liniowy	Związek monotoniczny (na rangach)	Związek monotoniczny (na parach)
Typ danych	Ilościowe, rozkład normalny	Rangi lub dane porządkowe/ilościowe	Rangi lub dane porządkowe/ilościowe
Wrażliwość na odstające	Wysoka	Mniejsza	Niska
Zakres wartości	–1 do 1	–1 do 1	–1 do 1
Wymagana liniowość	Tak	Nie	Nie
Odporność na wiązania	Niska	Średnia	Wysoka
Interpretacja	Siła i kierunek związku liniowego	Siła i kierunek monotonicznego związku	Proporcja par zgodnych vs niezgodnych
Test istotności	Tak (`scipy.stats.pearsonr`)	Tak (`spearmanr`)	Tak (`kendalltau`)

Krótkie podsumowanie:

Pearson – najlepszy, gdy dane są normalne i zależność jest liniowa.
Spearman – działa lepiej dla nieliniowych zależności monotonicznych.
Kendall – bardziej konserwatywny, często używany w badaniach społecznych, mniejsza wrażliwość na małe zmiany w danych.

Heatmapa korelacji rangowych¶

corr_kendall = df_pokemon.corr(method='kendall', numeric_only=True)
plt.figure(figsize=(10, 8))
sns.heatmap(corr, 
            annot=True,         
            fmt=".2f",          
            cmap="coolwarm",    
            vmin=-1, vmax=1,    
            square=True,       
            linewidths=0.5,   
            cbar_kws={"shrink": .75})  

plt.title("Macierz korelacji rangowych", fontsize=16)
plt.tight_layout()
plt.show()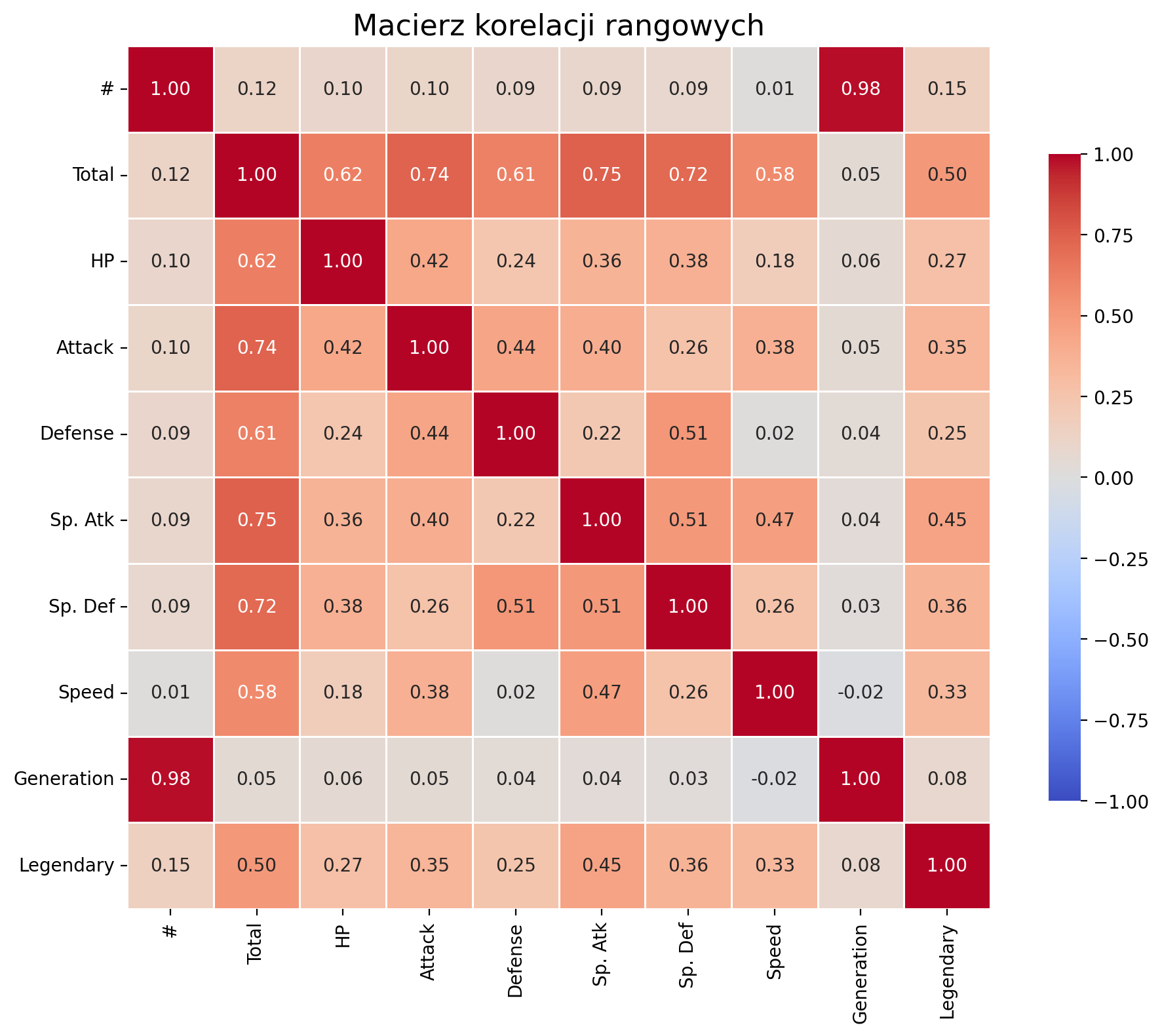

Twoja kolej¶

Dla zbioru danych o Pokemonach znajdź takie pary zmiennych, dla których najodpowiedniejsze będzie zastosowanie po jednej z miar korelacji ilościowej. Oblicz je, a następnie zwizualizuj.

from scipy.stats import pearsonr, spearmanr, kendalltau

## Twój kod tutaj

Korelacja zmiennych jakościowych¶

Zmienna jakościowa (kategoryczna) to taka, która przyjmuje wartości opisowe, reprezentujące kategorie — np. typ Pokémona (Fire, Water, Grass), płeć, status (Legendary vs Normal), itp.

Zmiennych takich nie można bezpośrednio analizować metodami korelacji dla liczb (Pearson, Spearman, Kendall). Zamiast tego stosuje się inne techniki.

Tabela kontyngencji¶

Tabela kontyngencji (ang. contingency table) to specjalna tabela krzyżowa, która pokazuje liczebność (czyli liczbę przypadków) dla wszystkich możliwych kombinacji dwóch zmiennych kategorycznych.

To podstawowe narzędzie do analizy zależności pomiędzy cechami jakościowymi.

Test Chi-kwadrat niezależności¶

Test Chi-kwadrat sprawdza, czy istnieje statystycznie istotna zależność między dwiema zmiennymi kategorycznymi.

Idea:

Porównujemy:

wartości zaobserwowane (z tabeli kontyngencji),
z wartościami oczekiwanymi, gdyby zmienne były niezależne.

\chi^2 = \sum \frac{(O_{ij} - E_{ij})^2}{E_{ij}}

(17)

Gdzie:

$O_{ij}$ – liczba zaobserwowana w komórce ( $i$ , $j$ ),
$E_{ij}$ – liczba oczekiwana w komórce ( $i$ , $j$ ), przy założeniu niezależności.

Tabela: Przykład kontyngencji – Type 1 vs Legendary

Type 1	Legendary = False	Legendary = True
Fire	18	5
Water	25	3
Grass	20	2
...	...	...

Interpretacja wyniku testu Chi-kwadrat:

Wartość	Znaczenie
Wysoka wartość χ²	Duża różnica między obserwacją a oczekiwaniem
Niska wartość p	Silna podstawa do odrzucenia hipotezy niezależności
p < 0.05	Istotna statystycznie zależność między zmiennymi

Korelacje jakościowe¶

V Cramer’a¶

V Cramér’a to miara siły zależności między dwiema zmiennymi jakościowymi (kategorycznymi). Bazuje na teście Chi-kwadrat, ale wynik jest przeskalowany do zakresu 0–1, dzięki czemu łatwo interpretuje się siłę związku.

V = \sqrt{ \frac{\chi^2}{n \cdot (k - 1)} }

(18)

Gdzie:

$\chi^2$ – statystyka testu chi-kwadrat,
$n$ – liczba obserwacji,
$k$ – mniejsza z liczby kategorii (wiersze/kolumny) w tabeli kontyngencji.

Współczynnik Phi ( $φ$ )¶

Zastosowanie:

Obie zmienne muszą być dychotomiczne (np. Tak/Nie, 0/1), a więc tabela musi mieć najmniejszy rozmiar 2x2!
Idealny do analizy np. płeć vs czy kupił, typ vs legendary.

\phi = \sqrt{ \frac{\chi^2}{n} }

(19)

Gdzie:

$\chi^2$ – statystyka testu chi-kwadrat dla tabeli 2×2,
$n$ – liczba obserwacji.

T Tschuprow’a¶

T Tschuprow’a to miara zależności, która jest stosunkowo podobna do V Cramér’a, ale ma inną skalę. Używana głównie w przypadkach, kiedy liczba kategorii w dwóch zmiennych jest zróżnicowana. Jest to bardziej zaawansowana miara, którą można stosować w szerszym zakresie tabel kontyngencji.

T = \sqrt{\frac{\chi^2}{n \cdot (k - 1)}}

(20)

Gdzie:

$\chi^2$ – statystyka testu chi-kwadrat,
$n$ – liczba obserwacji,
$k$ – mniejsza liczba kategorii (wiersze lub kolumny) w tabeli kontyngencji.

Zastosowanie: T Tschuprow’a jest użyteczne, gdy mamy do czynienia z tabelami kontyngencji o różnej liczbie kategorii w wierszach i kolumnach.

Podsumowanie - korelacje jakościowe¶

Miara	Co mierzy	Zastosowanie	Zakres wartości	Interpretacja siły
V Cramér’a	Siła związku między zmiennymi nominalnymi	Dowolne kategorie	0 – 1	0.1–słaba, 0.3–umiark., >0.5–silna
Phi ( $φ$ )	Siła związku w tabeli 2×2	Dwie zmienne binarne	-1 – 1	Podobnie jak korelacja
T Tschuprow’a	Siła zależności, alternatywa do Cramér’s V	Tabele o podobnej liczbie kategorii	0 – 1	Rzadziej używana
Chi² ( $χ²$ )	Test statystyczny niezależności	Wszystkie zmienne kategoryczne	0 – ∞	Im wyższy, tym silniejsza różnica

Przykład¶

Zbadajmy, czy typ Pokémona (type_1) jest zależny od tego, czy Pokémon jest legendarny (legendary).

Wykorzystamy bibliotekę scipy.

W tej bibliotece masz już wbudowane funkcje do obliczania różnych miar korelacji jakościowych.

from scipy.stats.contingency import association

# Tabela kontyngencji
ct = pd.crosstab(df_pokemon["Type 1"], df_pokemon["Legendary"])

# Obliczanie miary V Cramér'a
V = association(ct, method="cramer") # https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.contingency.association.html#association

print(f"V Cramer'a: {V}") # zinterpretuj!

V Cramer'a: 0.3361928228447545

Twoja kolej¶

Jaka wizualizacja byłaby najodpowiedniejsza do przedstawienia zalezności ilościowej, rangowej, a jaka do jakościowej?

Spróbuj na podstawie danych Pokemonów zastanowić się, jakie pary zmiennych mogłyby mieć jaki typ analizy.

## Twój kod i dyskusja tutaj

Heatmapa korelacji jakościowych¶

#!git clone https://github.com/ayanatherate/dfcorrs.git  #tylko raz!

from dfcorrs.cramersvcorr import Cramers
cram=Cramers()
cram.corr(df_pokemon)
cram.corr(df_pokemon, plot_htmp=True)

Podsumowanie¶

Istnieje wiele sposobów na opisanie naszych danych:

Pomiar tendencji centralnej.
Pomiar ich zmienności; skośności i kurtozy.
Pomiar tego, jakie korelacje zachodzą między naszymi danymi.

Wszystkie z nich są przydatne i wszystkie są również eksploracyjną analizą danych (EDA).

Odpowiedzi testu dot. skal:¶

SAD 2025

08 - Data preprocessing

09 - Statystyki opisowe

Skale pomiarowe w statystyce¶

Tabela: Skale pomiarowe w statystyce¶

Quiz: Skale pomiarowe w statystyce¶

1. Która ze skal umożliwia porządkowanie danych, ale nie ma równych odstępów?¶

2. Przykładem zmiennej w skali nominalnej jest:¶

3. Która skala nie ma zera absolutnego, ale posiada równe odstępy?¶

4. Jakie operacje są dozwolone na zmiennych w skali porządkowej?¶

5. Zmienna "class" w zbiorze Titanic (First, Second, Third) to przykład:¶

Statystyka opisowa¶

W tym rozdziale¶

Tendencja centralna¶

Dlaczego jest to przydatne?¶

Średnia arytmetyczna¶

numpy.mean¶

Obliczanie średniej kolumny pandas¶

Twoja kolej¶

Średnia i skośność¶

Twoja kolej¶

Twoja kolej¶

Podsumowanie pierwszej części¶

Mediana¶

Porównanie mediany i średniej¶

Twoja kolej¶

Moda¶

mode() zwraca wiele wartości?¶

Miary tendencji centralnej - podsumowanie¶

Kwantyle¶

Definicja¶

Wzór (dla uporządkowanego zbioru danych)¶

Przykład - obliczamy na piechotę¶

Decyle¶

Percentyle¶

Kwantyle - podsumowanie¶

Przykład - obliczamy kwantyle¶

Twoja kolej!¶

Zmienność¶

średnia ukrywa wariancję¶

Wykrywanie zmienności¶

Rozstęp¶

IQR¶

Wariancja i odchylenie standardowe¶

SD, objaśnione¶

Obliczanie SD w pandas¶

Uwaga na np.std¶

Współczynnik zmienności (CV)¶

Odchylenie międzykwartylowe¶

Twoja kolej!¶

Miary kształtu rozkładu¶

Skośność¶

Ujemna skośność¶

Zerowa skośność¶

Dodatnia skośność¶

Twoja kolej¶

Skośność międzykwartylowa¶

Twoja kolej!¶

Kurtoza¶

Zakres referencyjny dla kurtozy¶

Krzywa mezokurtyczna¶

Krzywa platykurtyczna¶

Krzywa leptokurtyczna¶

Kurtoza międzykwartylowa¶

Twoja kolej!¶

Podsumowanie statystyk¶

Analiza przekrojowa¶

Analiza korelacji¶

Korelacje ilościowe¶

Zależności liniowe: wysokość¶

Wykreślanie danych Pearsona dotyczących wysokości¶

Wprowadzenie do korelacji liniowych¶

Twoja kolej¶

Ograniczenia rrr Pearsona¶

Nieliniowe dane z r=0r = 0r=0¶

Gdy rrr jest niezmienny względem rzeczywistej relacji¶

Heatmapa¶

Twoja kolej¶

Korelacje rangowe¶

Typy korelacji rangowych¶

Kiedy stosować korelacje rangowe?¶

Interpretacja wartości korelacji¶

5. Zmienna `"class"` w zbiorze Titanic (`First`, `Second`, `Third`) to przykład:¶

`numpy.mean`¶

Obliczanie `średniej` kolumny `pandas`¶

Porównanie `mediany` i `średniej`¶

`mode()` zwraca wiele wartości?¶

`średnia` ukrywa wariancję¶

Obliczanie SD w `pandas`¶

Uwaga na `np.std`¶

Zależności liniowe: `wysokość`¶

Ograniczenia $r$ Pearsona¶

Nieliniowe dane z $r = 0$ ¶

Gdy $r$ jest niezmienny względem rzeczywistej relacji¶

Współczynnik Phi ( $φ$ )¶