10 - Sampling - SAD 2025

Ważne biblioteki¶

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns 
import pandas as pd
import scipy.stats as ss
from matplotlib.patches import Circle
import matplotlib.patches as patches

%matplotlib inline 
%config InlineBackend.figure_format = 'retina'

## Koncepcja samplingu

exec(open('sampling_pic.py').read())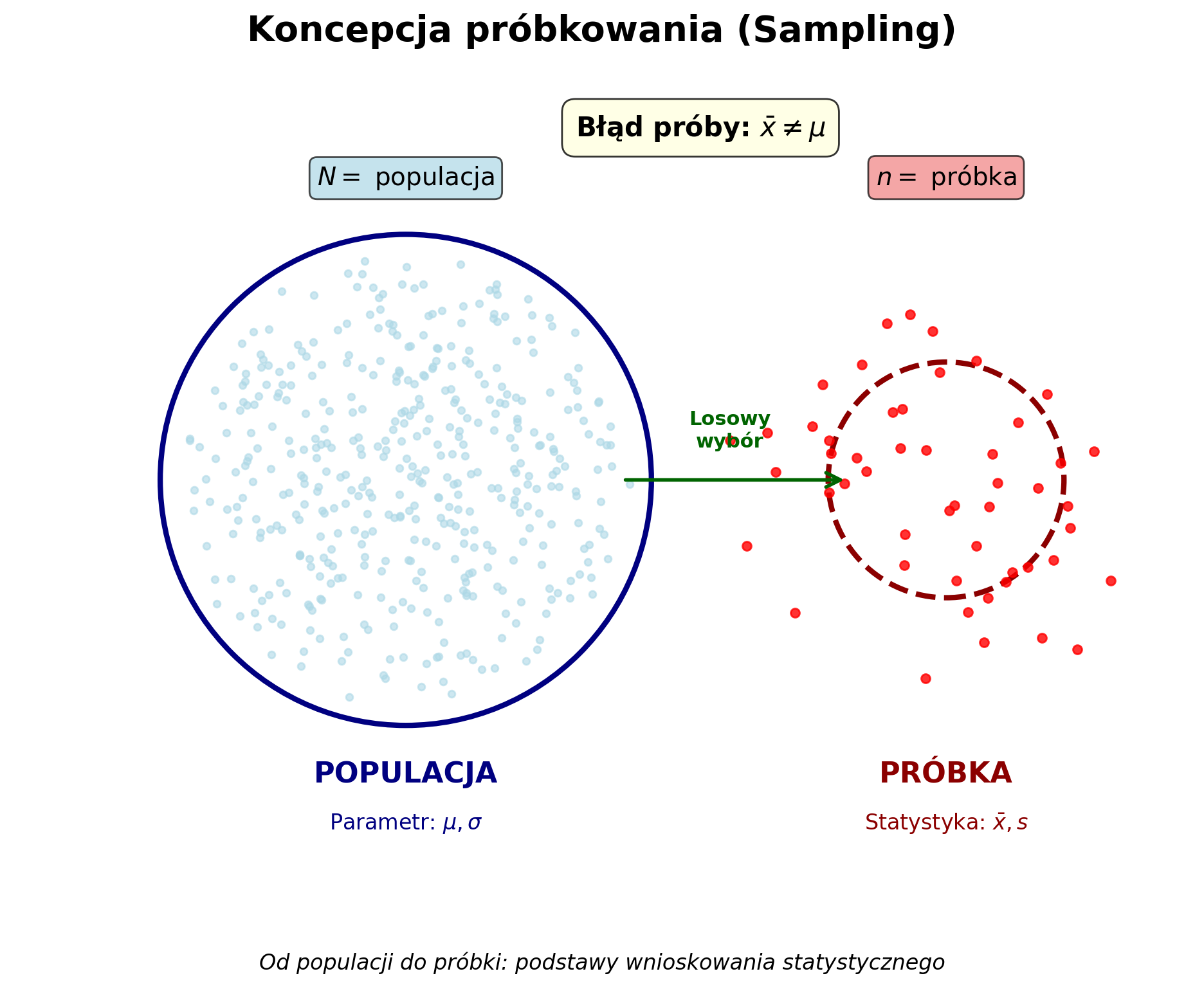

Cele tego rozdziału¶

Jest to ostatni wykład przed przejściem do modelowania statystycznego.

Ma on kilka celów:

Przejście od czysto statystyki opisowej (średnia itp.) do wnioskowania statystycznego.
- Rozróżnienie między próbkami a populacjami.
- Rozpoznawanie błędu próby.
Błąd standardowy i podstawy rozkładów próbnych.

Statystyka opisowa a wnioskowanie statystyczne¶

W „zestawie narzędzi” statystyki znajdują się co najmniej dwie półki:

Statystyka opisowa: opisuje posiadane dane (np. średnia, mediana, odchylenie standardowe itp.).
Statystyka matematyczna: próbuje uogólnić posiadane dane na szerszą populację.

Próbki a populacje¶

W statystyce populacja to zbiór potencjalnych obserwacji, które nas interesują. Pełen n z N zbiór.

Rzadko zdarza się, abyśmy mogli obserwować całą populację, która nas interesuje, chyba że jest ona bardzo wąska.

Na przykład „wszyscy ludzie na świecie” to bardzo szeroka populacja.
Nawet „wszyscy studenci PG” to duża populacja.

Dlatego zazwyczaj opieramy się na próbie.

Próba to rzeczywisty zbiór obserwacji pobranych z populacji.

Wyzwanie związane z uogólnianiem¶

Aby dokonać uogólnienia, próbki muszą być losowe i reprezentatywne.

W przeciwnym razie możemy nadmiernie reprezentować lub niedostatecznie reprezentować niektóre subpopulacje.

Niestety, wiele próbek to „próbki wygodne” – czyli te, które są dostępne w danym momencie.

Pytanie 1.¶

Jaki przykład z wcześniejszej części zajęć pokazuje, jak niereprezentatywna próba może prowadzić do obciążonych modeli?

Błąd próby: kolejne wyzwanie¶

Nawet jeśli próba jest reprezentatywna, nigdy nie jest identyczna z populacją bazową.

Błąd próby oznacza, że statystyki obliczone na podstawie próby (np. średnia) rzadko (o ile w ogóle) będą identyczne z parametrem populacji bazowej.

Średnia z próby¶

Średnia próby ( $\bar{X}$ ) rzadko, jeśli w ogóle, będzie identyczna ze średnią populacji ( $\mu$ ).

Symulacja 1.¶

## Najpierw należy utworzyć „populację”.
np.random.seed(10)
pop = np.random.normal(loc = 0, scale = 3, size = 1000)
pop.mean()

np.float64(-0.04366990684641133)

## Teraz pobierz próbkę z tej populacji za pomocą np.sample
sample = np.random.choice(pop, size = 100)
sample.mean()

np.float64(-0.17870546982513766)

Pytanie 2.¶

Co by było, gdybyśmy pobrali kilka próbek z naszej populacji, wszystkie tej samej wielkości, i obliczyli średnią każdej próbki?

Jak moglibyśmy nazwać ten zestaw statystyk próbek?
Jak myślisz, co byłoby prawdą w odniesieniu do „średniej” tego zestawu statystyk próbek?

Odpowiedź¶

Nazywa się to rozkładem próbkowym.

Ten rozkład próbkowy będzie miał rozkład normalny wokół rzeczywistej średniej populacyjnej!

Wprowadzenie do rozkładów z próby¶

Rozkład z próby to rozkład statystyk próbnych (np. średniej) pobranych ze wszystkich możliwych prób o wielkości $n$ .

Rozkłady próbkowe w praktyce¶

Najpierw symulujemy naszą podstawową populację bazową.

np.random.seed(seed=10)
pop = np.random.normal(loc = 65, scale = 3, size = 5000)
g = sns.histplot(pop)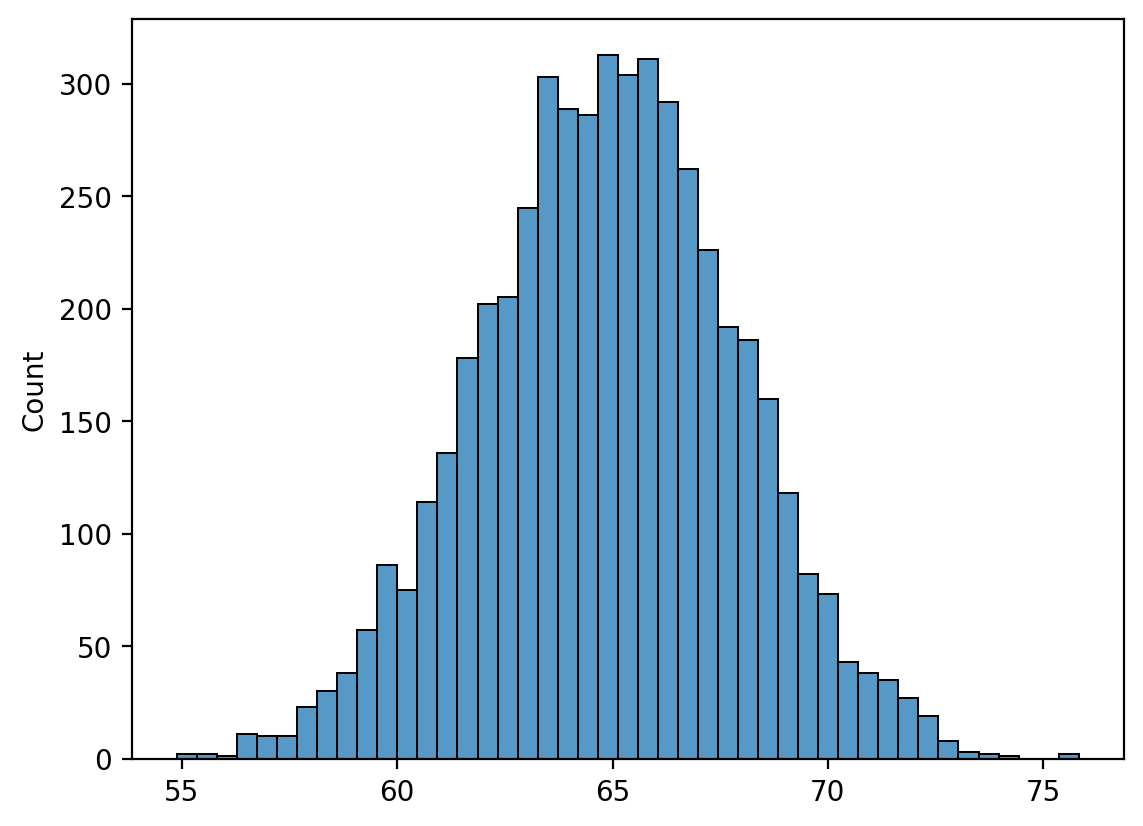

Tworzenie rozkładu próby¶

Teraz pobieramy próbki z tej populacji 300 razy, przy czym wielkość każdej próbki wynosi $n = 5$ .

Co zauważamy w rozkładzie średnich tych próbek? (Należy pamiętać, że nie jest to „prawdziwy” rozkład próby, ponieważ nie obejmuje on wszystkich możliwych próbek).

sample_means_n5 = []
for _ in range(300):
    sample = np.random.choice(pop, size = 5, replace = False)
    sample_means_n5.append(sample.mean())
    
g = sns.histplot(sample_means_n5)
plt.xlabel("Średnia z próby (n = 5)")
plt.axvline(pop.mean(), linestyle = "dotted", color = "red");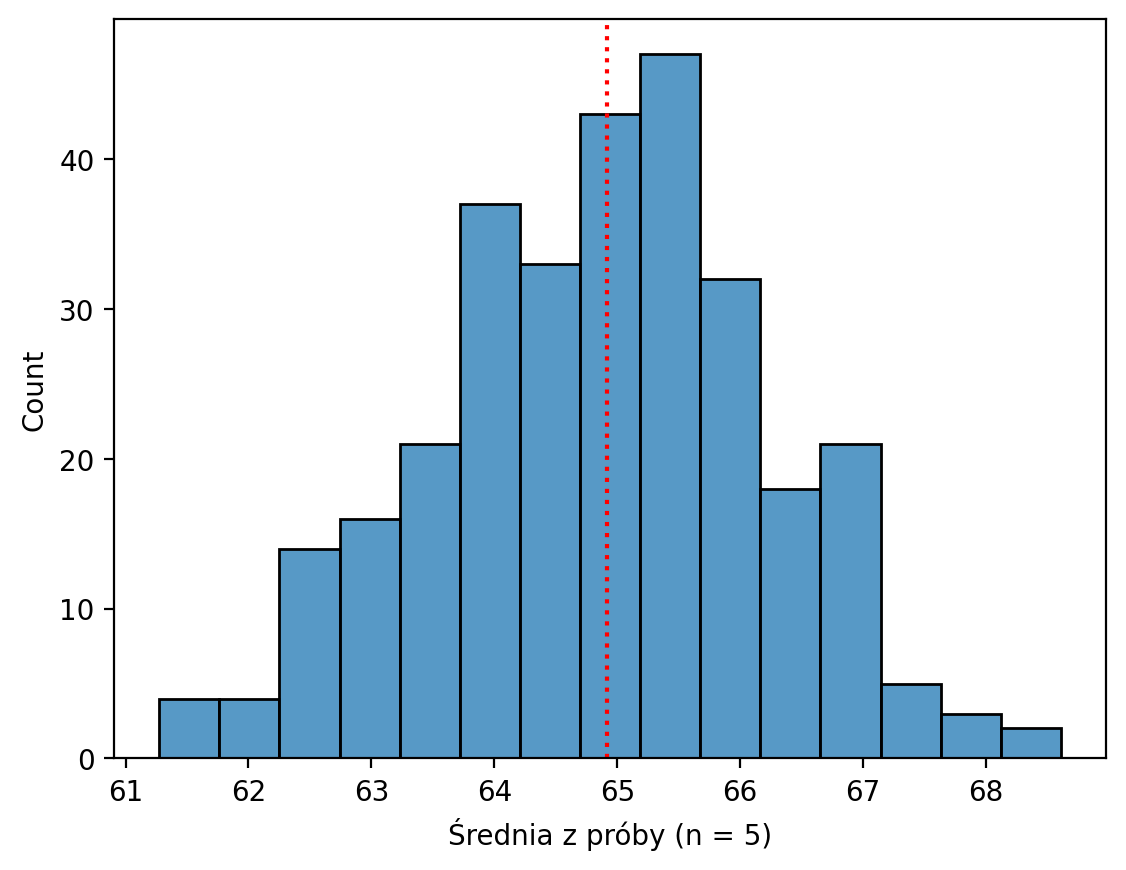

Dlaczego $n$ ma znaczenie¶

Porównajmy teraz kilka rozkładów:

Populacja pierwotna
Rozkład próby przy $n = 15$
Rozkład próby przy $n = 40$

Tworzenie nowego rozkładu próbkowania, gdzie $n=40$ ¶

sample_means_n40 = []
for _ in range(300):
    sample = np.random.choice(pop, size = 40, replace = False)
    sample_means_n40.append(sample.mean())

Wizualizacja obok siebie¶

Co zauważamy w rozkładzie próbkowania, gdy $n$ staje się większe?

# Teraz wizualizujemy je wszystkie razem.
f, (ax1, ax2, ax3) = plt.subplots(1, 3, sharex = True)
f.set_figwidth(9)
og = ax1.hist(pop, alpha = .5)
ax1.title.set_text("Populacja bazowa")
og_s1 = ax2.hist(sample_means_n5, alpha = .5)
ax2.title.set_text("Średnie z próbek (n = 5)")
og_s2 = ax3.hist(sample_means_n40, alpha = .5)
ax3.title.set_text("Średnie z próbek (n = 40)")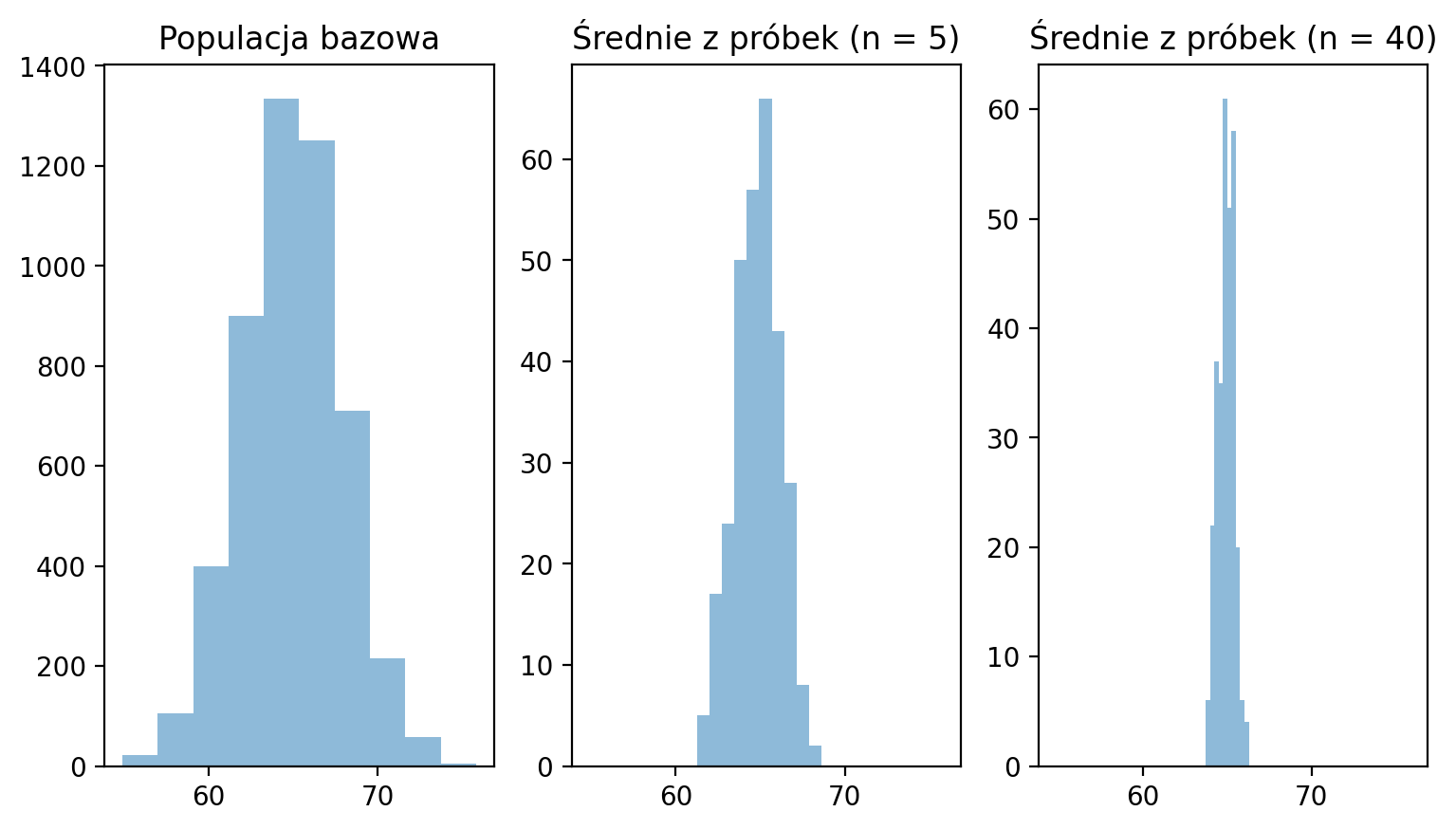

Dlaczego $n$ ma znaczenie (powtórka)¶

Wraz ze wzrostem wartości $n$ :

Rozkład próby staje się coraz bardziej normalny.
Wariancja naszego rozkładu próby maleje.

Jest to w istocie centralne twierdzenie graniczne.

Im większa próba, tym bardziej rozkład statystyki z próby zbliża się do rozkładu normalnego, nawet jeśli zmienna, którą mierzymy, nie posiada rozkładu normalnego.

Dotyczy to nawet rozkładów asymetrycznych!

Kwantyfikacja wariancji rozkładu próbkowego¶

Większa wartość $n$ powinna zwiększyć nasze przekonanie, że statystyka próbkowa jest dobrym przybliżeniem parametru populacyjnego.

Większa wartość $n$ oznacza mniejszą wariancję naszego rozkładu próbkowego.
To z kolei oznacza, że każda dana statystyka próbkowa jest stosunkowo bliska parametrowi populacyjnemu.

Jak możemy kwantyfikować wielkość wariancji w naszym hipotetycznym rozkładzie próbkowym?

Wprowadzenie pojęcia błędu standardowego¶

Błąd standardowy pozwala nam zmierzyć wariancję naszego rozkładu próbkowego.

Błąd standardowy (SE) definiuje się jako:

$\Large SE = \frac{s}{\sqrt{n}}$

Gdzie $s$ jest odchyleniem standardowym próby.

Pytanie 3.¶

Czym różni się błąd standardowy od odchylenia standardowego?

Błąd standardowy zależy od $n$ ¶

Odchylenie standardowe jest niezmienne względem wielkości naszej próby.
Błąd standardowy maleje wraz ze wzrostem wielkości próby ( $n$ ).
- SE odzwierciedla zarówno odchylenie standardowe, jak i $n$ .

Ns = np.linspace(1, 100, num = 100)
for sigma in [10, 20, 30, 40]:
    se = sigma / np.sqrt(Ns)
    plt.plot(Ns, se, label = r"$\sigma$ = {x}".format(x=sigma))  # Dodaj 'r' przed stringiem
plt.legend();
plt.xlabel("N");
plt.ylabel("Błąd standardowy");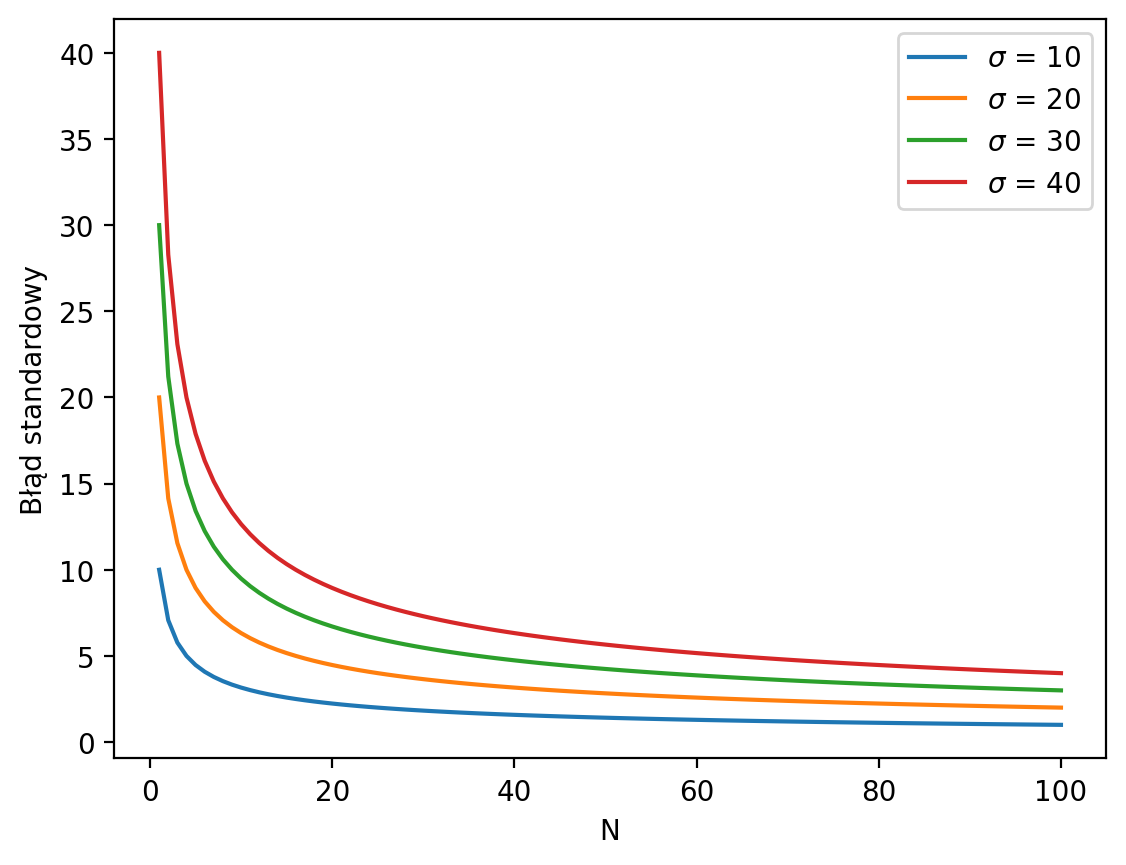

Obliczanie SE za pomocą `pandas`¶

pandas udostępnia funkcję (sem) do obliczania błędu standardowego średniej (SE) bezpośrednio w kolumnie.

df_height = pd.read_csv("data/wrangling/height.csv")
df_height['Father'].sem()

np.float64(0.08363032857029366)

Raportowanie błędu standardowego¶

Powszechną metodą wykorzystania błędu standardowego jest raportowanie go wraz ze średnią z próby:

Średnia z naszej próby wyniosła 25 USD, ± 3,5 (SE).

Symbol „±” oznacza po prostu pewną niepewność dotyczącą naszej statystyki próby.

## Koncepcja samplingu
exec(open('sampling_srednie.py').read())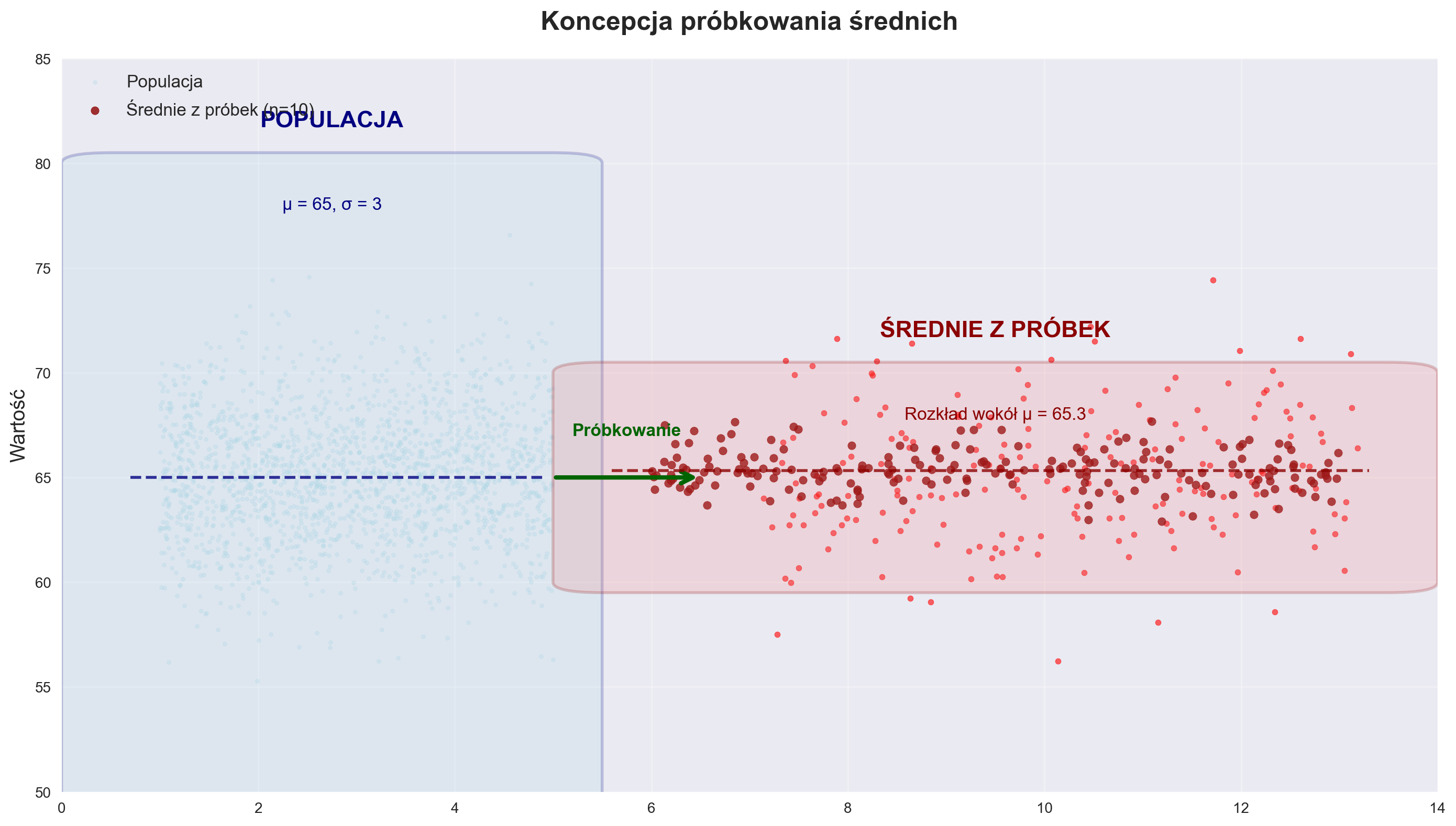

============================================================
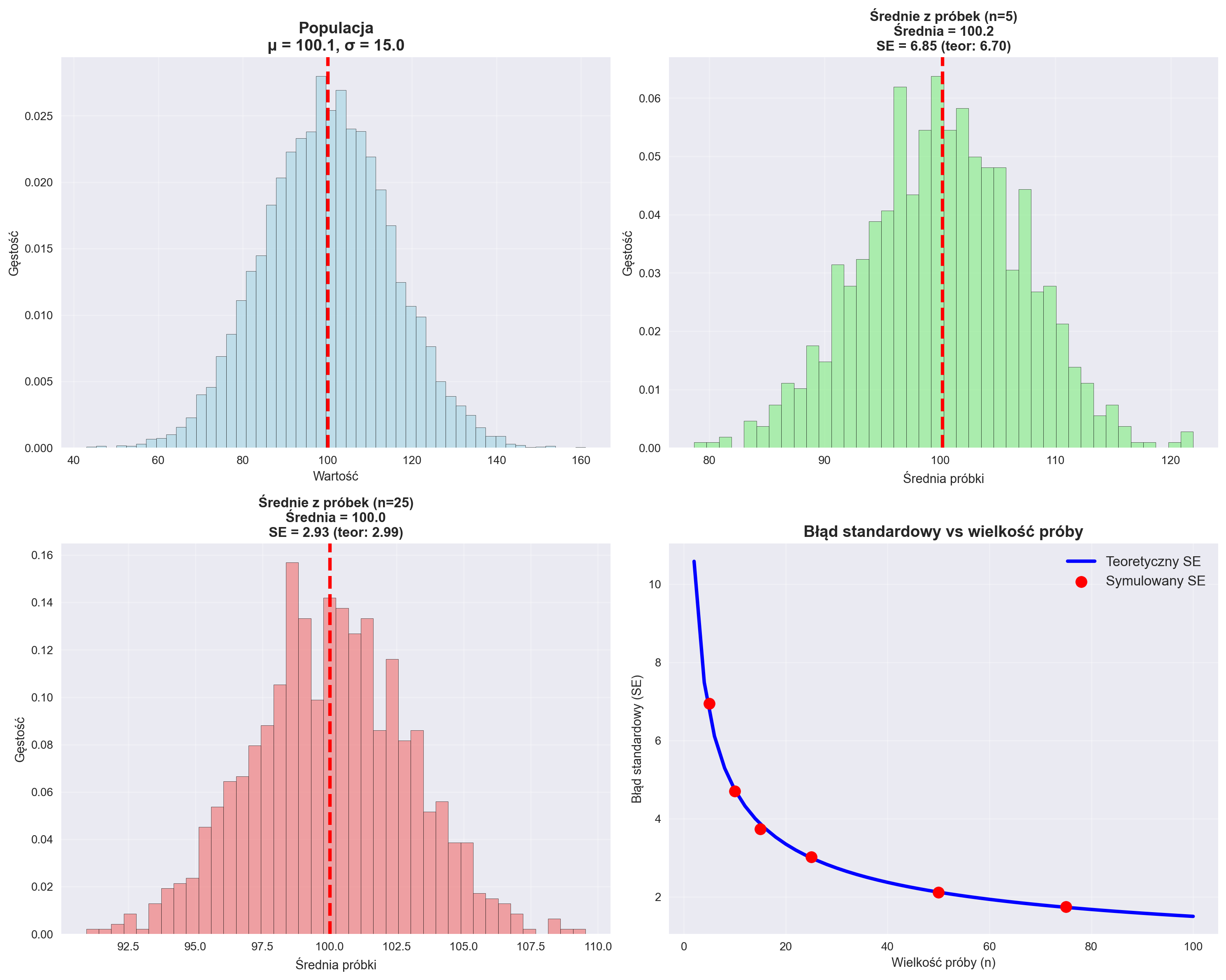
PODSUMOWANIE SYMULACJI PRÓBKOWANIA ŚREDNICH
============================================================
Populacja: μ = 100.15, σ = 14.97
Liczba symulacji: 1000 dla każdej wielkości próby

WYNIKI:
n=5:  Średnia próbkowa = 100.21, SE = 6.85
n=25: Średnia próbkowa = 100.02, SE = 2.93

WERYFIKACJA WZORU SE = σ/√n:
n=5:  SE teoretyczny = 6.70, SE empiryczny = 6.85
n=25: SE teoretyczny = 2.99, SE empiryczny = 2.93

Stosunek SE: 2.34 (teoretyczny: 2.24)

Podsumowanie - średnia z próby¶

To kończy nasze krótkie wprowadzenie do statystyki matematycznej.

Jego celem było przede wszystkim przedstawienie kilku kluczowych pojęć:

Błąd próby: statystyka próby ≠ parametr populacji.
Rozkłady próby: rozkład wszystkich statystyk próby z prób o wielkości $n$ .
Błąd standardowy: kwantyfikacja wariancji w naszym rozkładzie próby.

Wszystkie te pojęcia pomogą w przyszłych dyskusjach na temat modelowania statystycznego.

Rozkład normalny - teoria w kontekście Symulacji 1.¶

Definicja rozkładu normalnego¶

Rozkład normalny (zwany także rozkładem Gaussa) to jeden z najważniejszych rozkładów prawdopodobieństwa w statystyce. Jest to rozkład ciągły, który charakteryzuje się charakterystyczną krzywą w kształcie dzwonu.

Funkcja gęstości prawdopodobieństwa¶

Rozkład normalny opisuje wzór:

f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2}

(1)

gdzie:

$\mu$ – średnia (parametr położenia)
$\sigma$ – odchylenie standardowe (parametr skali)
$\sigma^2$ – wariancja

Zapisujemy to jako: $X \sim \mathcal{N}(\mu, \sigma^2)$

Właściwości rozkładu normalnego¶

Symetryczność – krzywa jest symetryczna względem średniej $\mu$
Kształt dzwonu – ma charakterystyczny kształt przypominający dzwon
Asymptoty – „ogony" krzywej zbliżają się do zera, ale nigdy jej nie osiągają
Reguła 68-95-99,7 (reguła trzech sigm):
- $68\%$ obserwacji mieści się w przedziale $[\mu - \sigma, \mu + \sigma]$
- $95\%$ obserwacji mieści się w przedziale $[\mu - 2\sigma, \mu + 2\sigma]$
- $99{,}7\%$ obserwacji mieści się w przedziale $[\mu - 3\sigma, \mu + 3\sigma]$

W kontekście Symulacji 1¶

W naszej symulacji:

Tworzymy populację z rozkładu normalnego: $\mathcal{N}(\mu=0, \sigma^2=9)$ , czyli $\sigma=3$
Pobieramy z niej próbki i obliczamy ich średnie
Rozkład średnich z próbek również będzie normalny (zgodnie z CTG)

Centralne Twierdzenie Graniczne (CTG)¶

Najważniejsze twierdzenie w kontekście rozkładu normalnego:

Niezależnie od kształtu rozkładu populacji, rozkład średnich z próbek o wystarczająco dużej wielkości $n$ będzie zbliżony do rozkładu normalnego.

Matematycznie:

\bar{X} \sim \mathcal{N}\left(\mu, \frac{\sigma^2}{n}\right)

(2)

gdzie:

$\bar{X}$ – średnia z próby
$\mu$ – średnia populacji
$\frac{\sigma^2}{n}$ – wariancja rozkładu próby (maleje wraz ze wzrostem $n$ !)

Błąd standardowy średniej¶

Błąd standardowy średniej to odchylenie standardowe rozkładu próby średnich:

SE(\bar{X}) = \sqrt{\frac{\sigma^2}{n}} = \frac{\sigma}{\sqrt{n}}

(3)

Standardowy rozkład normalny¶

Szczególny przypadek: $\mathcal{N}(0, 1)$ – rozkład o średniej 0 i odchyleniu standardowym 1.

Standaryzacja:

Z = \frac{X - \mu}{\sigma} \sim \mathcal{N}(0, 1)

(4)

Standaryzacja dla średniej z próby:

Z = \frac{\bar{X} - \mu}{\frac{\sigma}{\sqrt{n}}} = \frac{\bar{X} - \mu}{SE(\bar{X})} \sim \mathcal{N}(0, 1)

(5)

# Parametry rozkładu normalnego
mu = 0  # średnia
sigma = 1  # odchylenie standardowe

# Zakres wartości x
x = np.linspace(-4, 4, 1000)
y = stats.norm.pdf(x, mu, sigma)

# Tworzenie wykresu
fig, ax = plt.subplots(1, 1, figsize=(10, 6))

# Rysowanie krzywej gęstości
ax.plot(x, y, 'b-', linewidth=2, label=f'$\\mathcal{{N}}({mu}, {sigma}^2)$')

# Zakreskowanie obszarów zgodnie z regułą 68-95-99.7
# 68% - 1 sigma
x_1sigma = x[(x >= mu - sigma) & (x <= mu + sigma)]
y_1sigma = stats.norm.pdf(x_1sigma, mu, sigma)
ax.fill_between(x_1sigma, y_1sigma, alpha=0.3, color='green', 
                label='68% (±1σ)')

# 95% - 2 sigma  
x_2sigma = x[(x >= mu - 2*sigma) & (x <= mu + 2*sigma)]
y_2sigma = stats.norm.pdf(x_2sigma, mu, sigma)
ax.fill_between(x_2sigma, y_2sigma, alpha=0.2, color='orange',
                label='95% (±2σ)')

# 99.7% - 3 sigma
x_3sigma = x[(x >= mu - 3*sigma) & (x <= mu + 3*sigma)]
y_3sigma = stats.norm.pdf(x_3sigma, mu, sigma)
ax.fill_between(x_3sigma, y_3sigma, alpha=0.1, color='red',
                label='99.7% (±3σ)')

# Dodanie linii pionowych dla σ
for i in range(1, 4):
    ax.axvline(mu + i*sigma, color='gray', linestyle='--', alpha=0.7)
    ax.axvline(mu - i*sigma, color='gray', linestyle='--', alpha=0.7)
    ax.text(mu + i*sigma, 0.02, f'+{i}σ', ha='center', va='bottom')
    ax.text(mu - i*sigma, 0.02, f'-{i}σ', ha='center', va='bottom')

# Dodanie linii dla średniej
ax.axvline(mu, color='black', linestyle='-', linewidth=2, alpha=0.8)
ax.text(mu, 0.42, 'μ = 0', ha='center', va='bottom', fontsize=12, fontweight='bold')

# Formatowanie wykresu
ax.set_xlabel('Wartość zmiennej (x)', fontsize=12)
ax.set_ylabel('Gęstość prawdopodobieństwa f(x)', fontsize=12)
ax.set_title('Rozkład normalny $\\mathcal{N}(0, 1)$ z regułą 68-95-99.7', fontsize=14, fontweight='bold')
ax.legend(loc='upper right')
ax.grid(True, alpha=0.3)
ax.set_ylim(0, 0.45)

plt.tight_layout()
plt.show()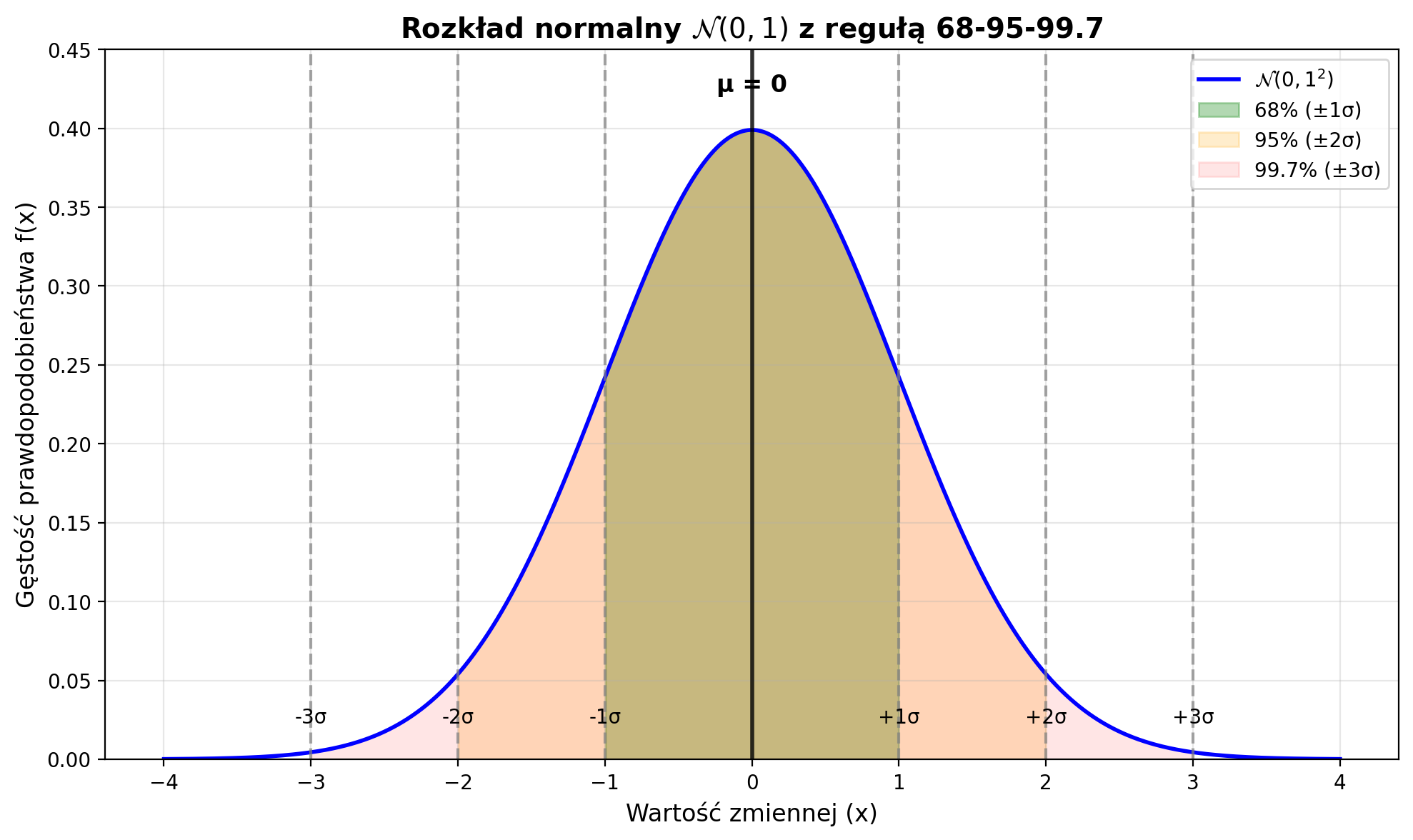

Rozkład t-Studenta¶

Rozkład t-Studenta (zwany także rozkładem Studenta) to jeden z najważniejszych rozkładów w statystyce praktycznej, szczególnie gdy nie znamy prawdziwego odchylenia standardowego populacji.

Dlaczego potrzebujemy rozkładu t-Studenta?¶

W praktyce rzadko znamy prawdziwe odchylenie standardowe populacji $\sigma$ . Zamiast tego musimy je estymować z próby używając $s$ (odchylenie standardowe próby).

Problem z rozkładem normalnym: Gdy używamy szacunku $s$ zamiast prawdziwego $\sigma$ , statystyka:

Z = \frac{\bar{X} - \mu}{\frac{s}{\sqrt{n}}}

(6)

nie ma już rozkładu normalnego $\mathcal{N}(0,1)$ !

Definicja rozkładu t-Studenta¶

Gdy populacja ma rozkład normalny, a $s$ jest odchyleniem standardowym z próby, to:

t = \frac{\bar{X} - \mu}{\frac{s}{\sqrt{n}}} \sim t_{n-1}

(7)

ma rozkład t-Studenta z $df = n-1$ stopniami swobody.

Funkcja gęstości prawdopodobieństwa¶

f(t) = \frac{\Gamma\left(\frac{\nu+1}{2}\right)}{\sqrt{\nu\pi}\,\Gamma\left(\frac{\nu}{2}\right)} \left(1+\frac{t^2}{\nu}\right)^{-\frac{\nu+1}{2}}

(8)

gdzie:

$\nu = n-1$ – liczba stopni swobody
$\Gamma$ – funkcja gamma

Właściwości rozkładu t-Studenta¶

Symetryczny względem zera (podobnie jak rozkład normalny)
Grubsze ogony niż rozkład normalny (większe prawdopodobieństwo wartości ekstremalnych)
Kształt zależy od stopni swobody $\nu = n-1$
Zbieżność do rozkładu normalnego: gdy $n \to \infty$ , rozkład $t_{\nu} \to \mathcal{N}(0,1)$

Parametry rozkładu¶

Średnia: $E[t] = 0$ (dla $\nu > 1$ )
Wariancja: $\text{Var}(t) = \frac{\nu}{\nu-2}$ (dla $\nu > 2$ )
Odchylenie standardowe: $\sigma_t = \sqrt{\frac{\nu}{\nu-2}}$

Zastosowania w praktyce¶

Rozkład t-Studenta używamy gdy:

Nie znamy prawdziwego odchylenia standardowego populacji $\sigma$
Próba jest względnie mała (zwykle $n < 30$ )
Chcemy konstruować przedziały ufności dla średniej
Przeprowadzamy testy t-Studenta

Przykładowy przedział ufności dla średniej:

\bar{x} \pm t_{\alpha/2, n-1} \cdot \frac{s}{\sqrt{n}}

(9)

gdzie $t_{\alpha/2, n-1}$ to wartość krytyczna z rozkładu t-Studenta.

Stopnie swobody w rozkładzie t-Studenta¶

Co to są stopnie swobody?¶

Stopnie swobody (degrees of freedom, df) to kluczowe pojęcie w statystyce, które określa liczbę niezależnych informacji dostępnych do oszacowania parametru statystycznego.

Definicja matematyczna¶

Stopnie swobody to liczba obserwacji w próbie minus liczba parametrów, które musimy oszacować z tej próby.

W przypadku średniej z próby:

df = n - 1

(10)

gdzie:

$n$ – wielkość próby
1 – liczba oszacowanych parametrów (średnia $\bar{x}$ )

Dlaczego odejmujemy 1?¶

Gdy obliczamy odchylenie standardowe próby $s$ , używamy wzoru:

s = \sqrt{\frac{\sum_{i=1}^{n}(x_i - \bar{x})^2}{n-1}}

(11)

Kluczowa obserwacja:

Mamy $n$ obserwacji: $x_1, x_2, \ldots, x_n$
Ale gdy znamy średnią $\bar{x}$ oraz $(n-1)$ odchyleń od średniej, to ostatnie odchylenie jest automatycznie określone!

Przykład intuicyjny¶

Wyobraź sobie próbę z $n = 3$ obserwacjami: $x_1, x_2, x_3$ .

Jeśli wiemy, że:

$\bar{x} = 5$
$(x_1 - \bar{x}) = -2$
$(x_2 - \bar{x}) = +1$

To automatycznie $(x_3 - \bar{x}) = +1$ , ponieważ suma odchyleń od średniej musi wynosić zero:

\sum_{i=1}^{n}(x_i - \bar{x}) = 0

(12)

Wpływ na rozkład t-Studenta¶

Im mniejsze stopnie swobody:

Tym grubsze ogony ma rozkład t-Studenta
Tym większa niepewność w naszych oszacowaniach
Tym bardziej ostrożni musimy być w wnioskach

Matematycznie:

\text{Var}(t) = \frac{\nu}{\nu-2} \text{ gdzie } \nu = df

(13)

Praktyczne znaczenie¶

Wielkość próby ( $n$ )	Stopnie swobody ( $df = n-1$ )	Charakterystyka rozkładu
$n = 2$	$df = 1$	Bardzo grube ogony, duża niepewność
$n = 5$	$df = 4$	Zauważalnie grubsze ogony niż normalny
$n = 30$	$df = 29$	Bardzo blisko rozkładu normalnego
$n = \infty$	$df = \infty$	Identyczny z rozkładem normalnym

Dlaczego to ważne?¶

Przedziały ufności są szersze dla małych $df$
Wartości krytyczne są większe dla małych $df$
Testy statystyczne są bardziej konserwatywne dla małych $df$

Przykład wartości krytycznych:

Dla $df = 4$ : $t_{0{,}025} = 2{,}78$
Dla $df = 29$ : $t_{0{,}025} = 2{,}05$
Dla rozkładu normalnego: $z_{0{,}025} = 1{,}96$

Wniosek: Im mniejsza próba, tym więcej “zapasu bezpieczeństwa” potrzebujemy w naszych wnioskach!

Wzór ogólny dla stopni swobody¶

W różnych kontekstach statystycznych:

df = n - k

(14)

gdzie:

$n$ – liczba obserwacji
$k$ – liczba oszacowanych parametrów

Przykłady:

Średnia z próby: $df = n - 1$ (oszacowujemy $\mu$ )
Regresja liniowa: $df = n - p - 1$ (oszacowujemy $p$ współczynników + wyraz wolny)
Test chi-kwadrat: $df = (r-1)(c-1)$ (w tabeli kontyngencji)

# Porównanie rozkładu normalnego z rozkładem t-Studenta
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# Parametry
x = np.linspace(-4, 4, 1000)

# Rozkład normalny standardowy
y_normal = stats.norm.pdf(x, 0, 1)

# Rozkłady t-Studenta z różnymi stopniami swobody
y_t1 = stats.t.pdf(x, df=1)
y_t3 = stats.t.pdf(x, df=3)
y_t10 = stats.t.pdf(x, df=10)
y_t30 = stats.t.pdf(x, df=30)

# Tworzenie wykresu
fig, ax = plt.subplots(1, 1, figsize=(12, 8))

# Rysowanie krzywych
ax.plot(x, y_normal, 'k-', linewidth=2, label='$\\mathcal{N}(0,1)$ (rozkład normalny)')
ax.plot(x, y_t1, 'r--', linewidth=2, label='$t_1$ (df = 1)')
ax.plot(x, y_t3, 'b--', linewidth=2, label='$t_3$ (df = 3)') 
ax.plot(x, y_t10, 'g--', linewidth=2, label='$t_{10}$ (df = 10)')
ax.plot(x, y_t30, 'm--', linewidth=2, label='$t_{30}$ (df = 30)')

# Zakreskowanie obszaru dla ilustracji grubszych ogonów
x_tail = x[x >= 2]
y_normal_tail = stats.norm.pdf(x_tail, 0, 1)
y_t3_tail = stats.t.pdf(x_tail, df=3)

ax.fill_between(x_tail, 0, y_normal_tail, alpha=0.3, color='gray', 
                label='Ogon rozkładu normalnego')
ax.fill_between(x_tail, 0, y_t3_tail, alpha=0.3, color='blue',
                label='Ogon rozkładu t (df=3)')

# Dodanie linii pionowych
ax.axvline(0, color='black', linestyle='-', alpha=0.3)
ax.axvline(2, color='red', linestyle=':', alpha=0.7)
ax.axvline(-2, color='red', linestyle=':', alpha=0.7)

# Annotacje
ax.annotate('Grubsze ogony\nw rozkładzie t', 
            xy=(2.5, 0.02), xytext=(3, 0.15),
            arrowprops=dict(arrowstyle='->', color='red'),
            fontsize=10, ha='center')

# Formatowanie wykresu
ax.set_xlabel('Wartość zmiennej', fontsize=12)
ax.set_ylabel('Gęstość prawdopodobieństwa', fontsize=12)
ax.set_title('Porównanie rozkładu normalnego z rozkładem t-Studenta', fontsize=14, fontweight='bold')
ax.legend(loc='upper right')
ax.grid(True, alpha=0.3)
ax.set_ylim(0, 0.4)

plt.tight_layout()
plt.show()

# Tabela porównawcza wariancji
print("Porównanie wariancji:")
print("Rozkład normalny N(0,1): σ² = 1.000")
for df in [1, 2, 3, 5, 10, 30]:
    if df > 2:
        var_t = df / (df - 2)
        print(f"Rozkład t-Studenta (df={df}): σ² = {var_t:.3f}")
    else:
        print(f"Rozkład t-Studenta (df={df}): σ² = nieskończona")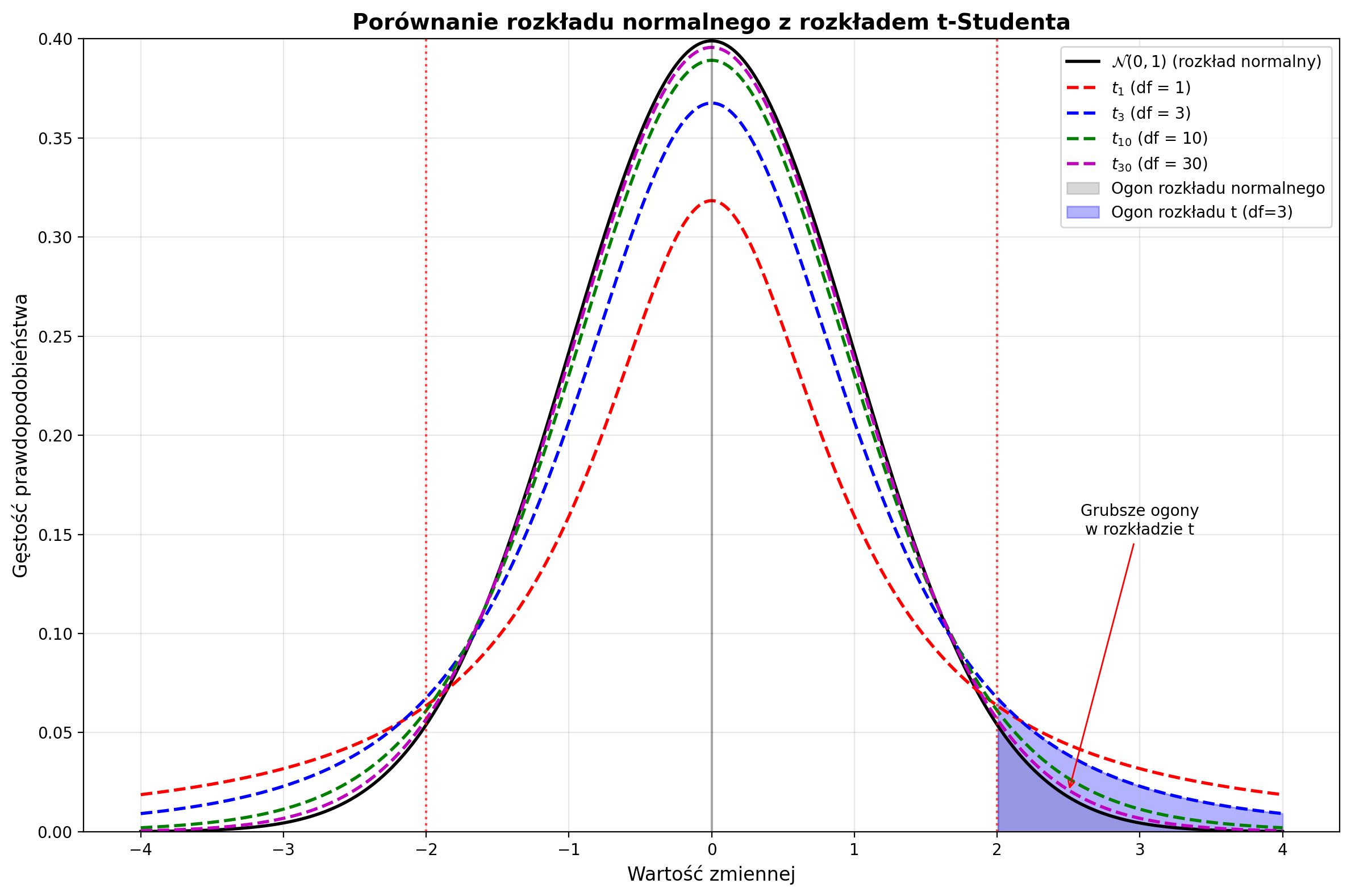

Porównanie wariancji:
Rozkład normalny N(0,1): σ² = 1.000
Rozkład t-Studenta (df=1): σ² = nieskończona
Rozkład t-Studenta (df=2): σ² = nieskończona
Rozkład t-Studenta (df=3): σ² = 3.000
Rozkład t-Studenta (df=5): σ² = 1.667
Rozkład t-Studenta (df=10): σ² = 1.250
Rozkład t-Studenta (df=30): σ² = 1.071

Proporcja z próby¶

Symulacja 2.¶

Załóżmy, że koszykarz wykonuje 10 rzutów (n=10) i trafia z prawdopodobieństwem 0,4 (prawdopodobieństwo sukcesu p=0,4).

Jeśli ten koszykarz wykona to ćwiczenie raz, możemy obliczyć liczbę sukcesów w następujący sposób

Rozkład dwumianowy w Symulacji 2.¶

W Symulacji 2. analizujemy klasyczny przykład rozkładu dwumianowego (ang. binomial distribution), który modeluje liczbę sukcesów w sekwencji niezależnych prób Bernoulliego.

Definicja i wzór¶

Rozkład dwumianowy opisuje prawdopodobieństwo uzyskania dokładnie $k$ sukcesów w $n$ niezależnych próbach, gdzie każda próba ma prawdopodobieństwo sukcesu równe $p$ .

Funkcja masy prawdopodobieństwa:

P(X = k) = \binom{n}{k} p^k (1-p)^{n-k}

(15)

gdzie:

$X$ – zmienna losowa oznaczająca liczbę sukcesów
$n = 10$ – liczba rzutów (prób)
$k \in \{0, 1, 2, \ldots, n\}$ – konkretna liczba trafień
$p = 0{,}4$ – prawdopodobieństwo trafienia w pojedynczym rzucie
$\binom{n}{k} = \frac{n!}{k!(n-k)!}$ – współczynnik dwumianowy

Parametry rozkładu¶

Dla rozkładu dwumianowego $X \sim \text{Binomial}(n, p)$ :

Wartość oczekiwana: $E[X] = np = 10 \times 0{,}4 = 4$
Wariancja: $\text{Var}(X) = np(1-p) = 10 \times 0{,}4 \times 0{,}6 = 2{,}4$
Odchylenie standardowe: $\sigma = \sqrt{np(1-p)} = \sqrt{2{,}4} \approx 1{,}55$

# Generuje losowe dwumianowe próbki
scoring_success_1 = np.random.binomial(n=10, p=0.4, size=1)
prob_1 = scoring_success_1 / 10

# Dziennie
scoring_success_10 = np.random.binomial(n=10, p=0.4, size=10)
prob_10 = scoring_success_10 / 10

# Tygodniowo
scoring_success_50 = np.random.binomial(n=10, p=0.4, size=50)
prob_50 = scoring_success_50 / 10

# Miesięcznie
scoring_success_200 = np.random.binomial(n=10, p=0.4, size=200)
prob_200 = scoring_success_200 / 10

# Rocznie
scoring_success_2600 = np.random.binomial(n=10, p=0.4, size=2600)
prob_2600 = scoring_success_2600 / 10

# Rysujemy histogramy
fig, axs = plt.subplots(4, 1, figsize=(10, 20))

axs[0].hist(prob_10, bins=5, edgecolor='k', alpha=0.7)
axs[0].set_title('Dzienne prawdopodobieństwo sukcesu')
axs[0].set_xlabel('Proporcja z próby')
axs[0].set_ylabel('Liczebność')

axs[1].hist(prob_50, bins=10, edgecolor='k', alpha=0.7)
axs[1].set_title('Tygodniowe prawdopodobieństwo sukcesu')
axs[1].set_xlabel('Proporcja z próby')
axs[1].set_ylabel('Liczebność')

axs[2].hist(prob_200, bins=10, edgecolor='k', alpha=0.7)
axs[2].set_title('Miesięczne prawdopodobieństwo sukcesu')
axs[2].set_xlabel('Proporcja z próby')
axs[2].set_ylabel('Liczebność')

axs[3].hist(prob_2600, bins=10, edgecolor='k', alpha=0.7)
axs[3].set_title('Roczne prawdopodobieństwo sukcesu')
axs[3].set_xlabel('Proporcja z próby')
axs[3].set_ylabel('Liczebność')

plt.tight_layout()
plt.show()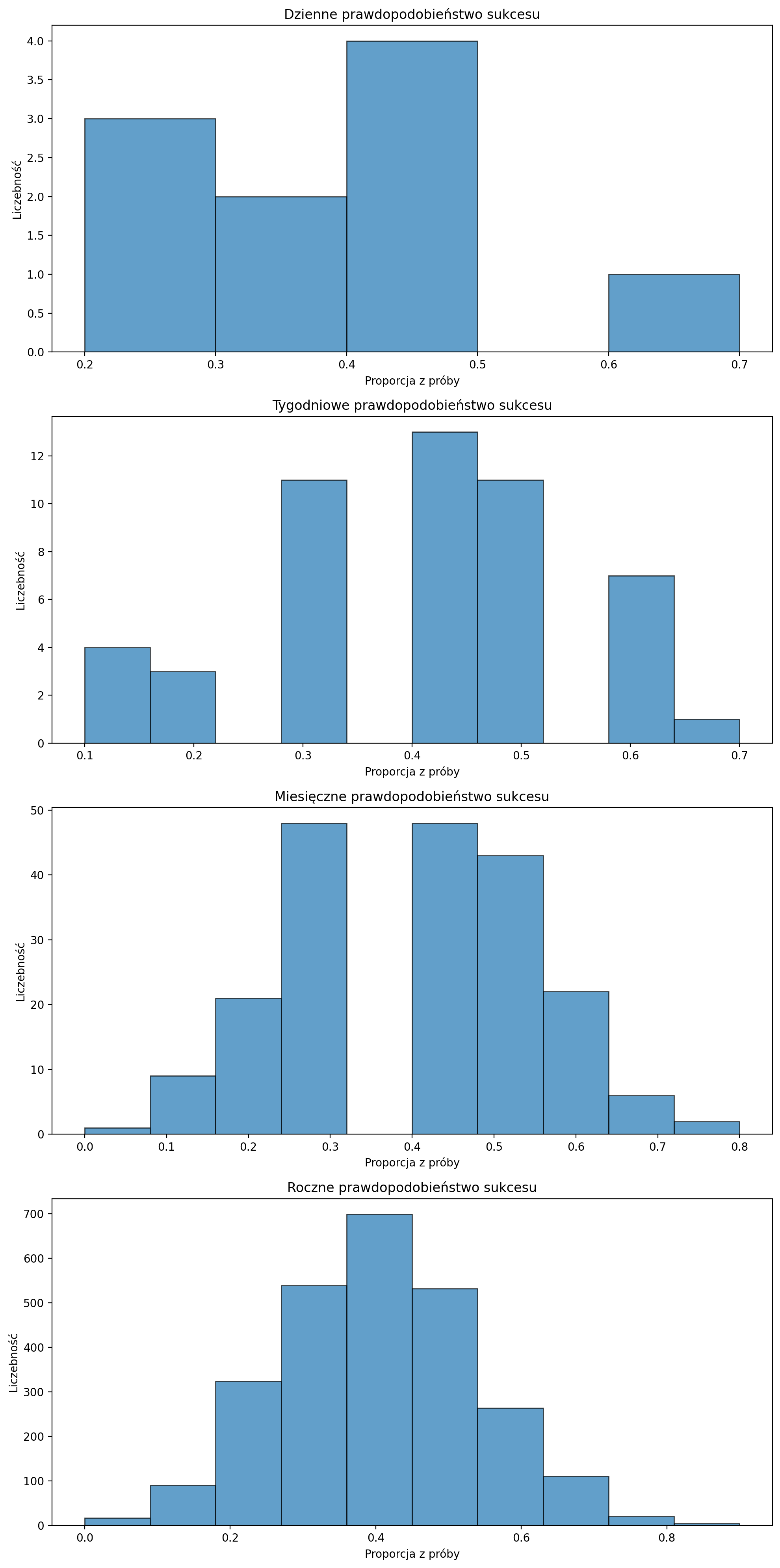

Proporcja z próby¶

W symulacji obliczamy proporcję sukcesów:

\hat{p} = \frac{X}{n}

(16)

gdzie $\hat{p}$ jest estymatorem prawdziwego prawdopodobieństwa $p = 0{,}4$ .

Centralne Twierdzenie Graniczne dla proporcji¶

Gdy liczba niezależnych eksperymentów rośnie, rozkład proporcji $\hat{p}$ zbliża się do rozkładu normalnego:

\hat{p} \xrightarrow{d} \mathcal{N}\left(p, \frac{p(1-p)}{n}\right)

(17)

czyli:

\hat{p} \sim \mathcal{N}\left(0{,}4, \frac{0{,}4 \times 0{,}6}{10}\right) = \mathcal{N}(0{,}4, 0{,}024)

(18)

Błąd standardowy proporcji:

SE(\hat{p}) = \sqrt{\frac{p(1-p)}{n}} = \sqrt{\frac{0{,}4 \times 0{,}6}{10}} = \sqrt{0{,}024} \approx 0{,}155

(19)

To właśnie obserwujemy na histogramach – wraz ze wzrostem liczby symulacji rozkład proporcji staje się coraz bardziej normalny i skupiony wokół prawdziwej wartości $p = 0{,}4$ .

Reguła 5¶

Przybliżenie normalne jest dokładne, gdy spełnione są warunki:

np \geq 5 \quad \text{i} \quad n(1-p) \geq 5

(20)

W naszym przypadku:

$np = 10 \times 0{,}4 = 4 < 5$ (nie spełnione)
$n(1-p) = 10 \times 0{,}6 = 6 \geq 5$ (spełnione)

To właśnie obserwujemy na histogramach – wraz ze wzrostem liczby symulacji rozkład proporcji staje się coraz bardziej normalny i skupiony wokół prawdziwej wartości $p = 0{,}4$ .

## Koncepcja samplingu - proporcje

exec(open('sampling_proporcje.py').read())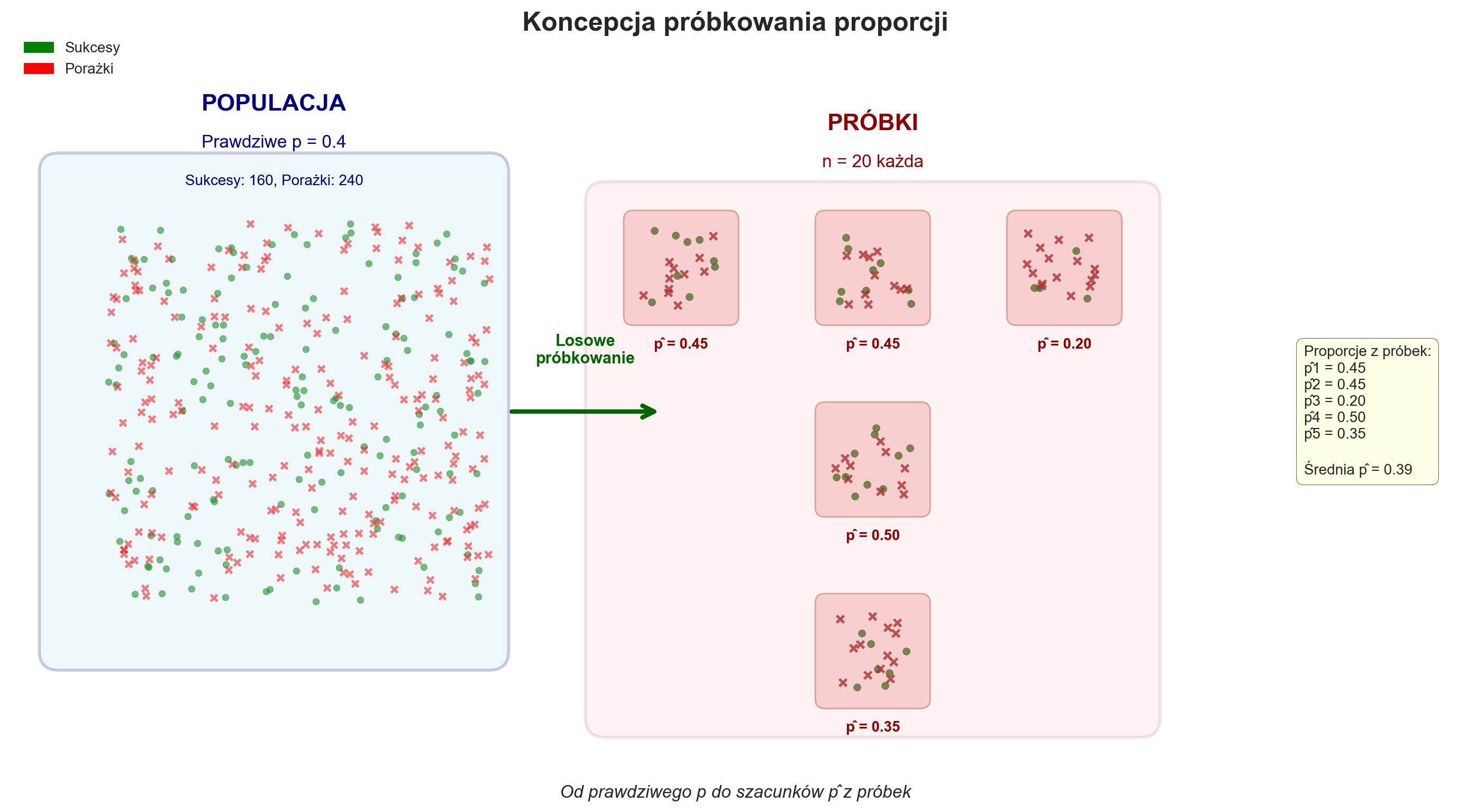

======================================================================
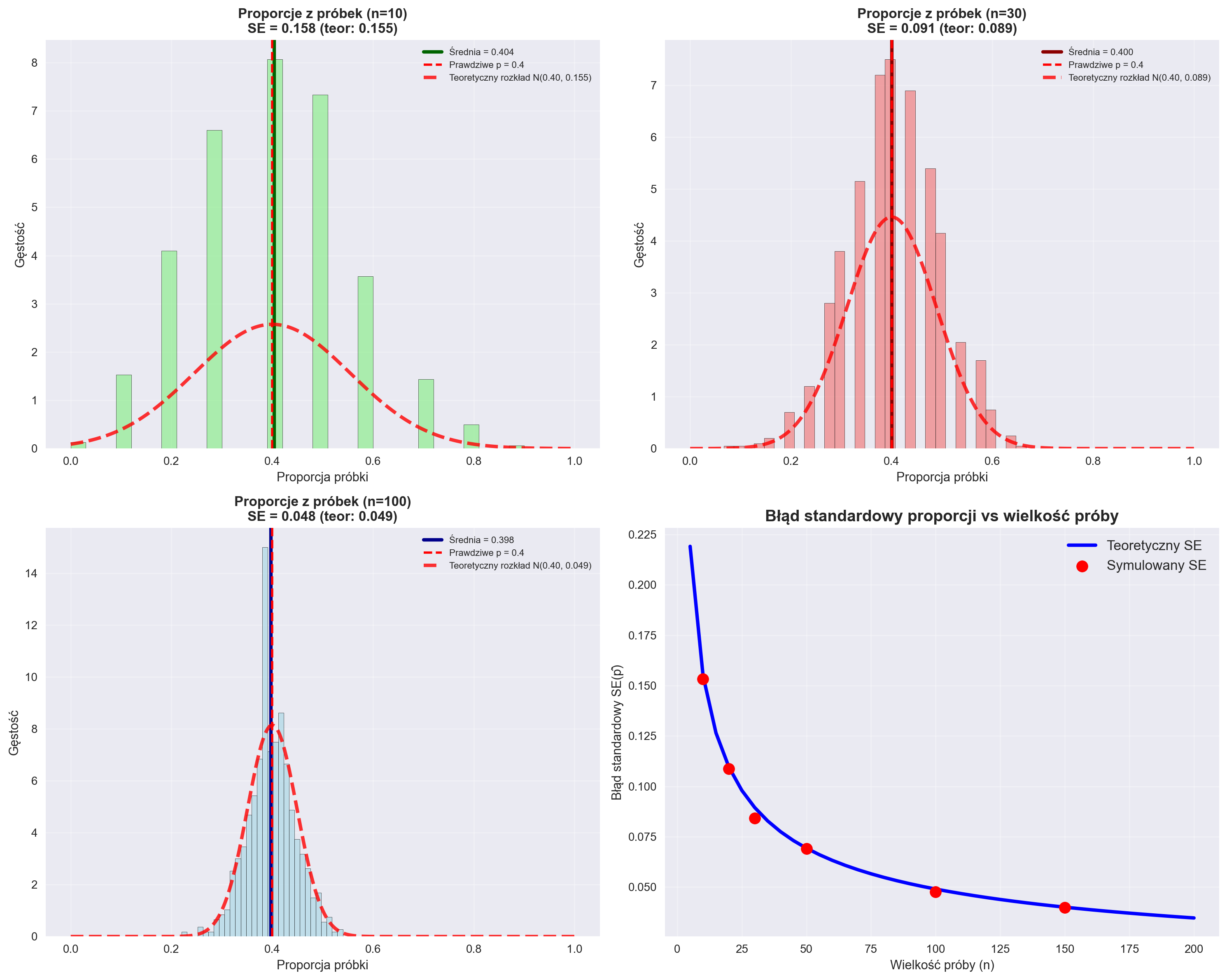
PODSUMOWANIE SYMULACJI PRÓBKOWANIA PROPORCJI
======================================================================
Prawdziwe p = 0.4
Liczba symulacji: 1000 dla każdej wielkości próby

WYNIKI:
n=10:  Średnia p̂ = 0.404, SE = 0.158
n=30:  Średnia p̂ = 0.400, SE = 0.091
n=100: Średnia p̂ = 0.398, SE = 0.048

WERYFIKACJA WZORU SE(p̂) = √[p(1-p)/n]:
n=10:  SE teoretyczny = 0.155, SE empiryczny = 0.158
n=30:  SE teoretyczny = 0.089, SE empiryczny = 0.091
n=100: SE teoretyczny = 0.049, SE empiryczny = 0.048

SPRAWDZENIE REGUŁY 5:
n=10: np = 4.0, n(1-p) = 6.0 → Reguła 5: ✗
n=30: np = 12.0, n(1-p) = 18.0 → Reguła 5: ✓
n=100: np = 40.0, n(1-p) = 60.0 → Reguła 5: ✓

SAD 2025

09 - Statystyki opisowe

SAD 2025

11 - Estymacja parametrów

10 - Sampling

Ważne biblioteki¶

Cele tego rozdziału¶

Statystyka opisowa a wnioskowanie statystyczne¶

Próbki a populacje¶

Wyzwanie związane z uogólnianiem¶

Pytanie 1.¶

Błąd próby: kolejne wyzwanie¶

Średnia z próby¶

Symulacja 1.¶

Pytanie 2.¶

Odpowiedź¶

Wprowadzenie do rozkładów z próby¶

Rozkłady próbkowe w praktyce¶

Tworzenie rozkładu próby¶

Dlaczego nnn ma znaczenie¶

Tworzenie nowego rozkładu próbkowania, gdzie n=40n=40n=40¶

Wizualizacja obok siebie¶

Dlaczego nnn ma znaczenie (powtórka)¶

Kwantyfikacja wariancji rozkładu próbkowego¶

Wprowadzenie pojęcia błędu standardowego¶

Pytanie 3.¶

Błąd standardowy zależy od nnn¶

Obliczanie SE za pomocą pandas¶

Raportowanie błędu standardowego¶

Podsumowanie - średnia z próby¶

Rozkład normalny - teoria w kontekście Symulacji 1.¶

Definicja rozkładu normalnego¶

Funkcja gęstości prawdopodobieństwa¶

Właściwości rozkładu normalnego¶

W kontekście Symulacji 1¶

Centralne Twierdzenie Graniczne (CTG)¶

Błąd standardowy średniej¶

Standardowy rozkład normalny¶

Rozkład t-Studenta¶

Dlaczego potrzebujemy rozkładu t-Studenta?¶

Definicja rozkładu t-Studenta¶

Funkcja gęstości prawdopodobieństwa¶

Właściwości rozkładu t-Studenta¶

Parametry rozkładu¶

Zastosowania w praktyce¶

Stopnie swobody w rozkładzie t-Studenta¶

Co to są stopnie swobody?¶

Definicja matematyczna¶

Dlaczego odejmujemy 1?¶

Przykład intuicyjny¶

Wpływ na rozkład t-Studenta¶

Praktyczne znaczenie¶

Dlaczego to ważne?¶

Wzór ogólny dla stopni swobody¶

Proporcja z próby¶

Symulacja 2.¶

Rozkład dwumianowy w Symulacji 2.¶

Definicja i wzór¶

Parametry rozkładu¶

Proporcja z próby¶

Centralne Twierdzenie Graniczne dla proporcji¶

Reguła 5¶

Dlaczego $n$ ma znaczenie¶

Tworzenie nowego rozkładu próbkowania, gdzie $n=40$ ¶

Dlaczego $n$ ma znaczenie (powtórka)¶

Błąd standardowy zależy od $n$ ¶

Obliczanie SE za pomocą `pandas`¶