11 - Estymacja parametrów

Estymacja punktowa i przedziałowa¶

Estymacja średniej¶

exec(open('est_p.py').read())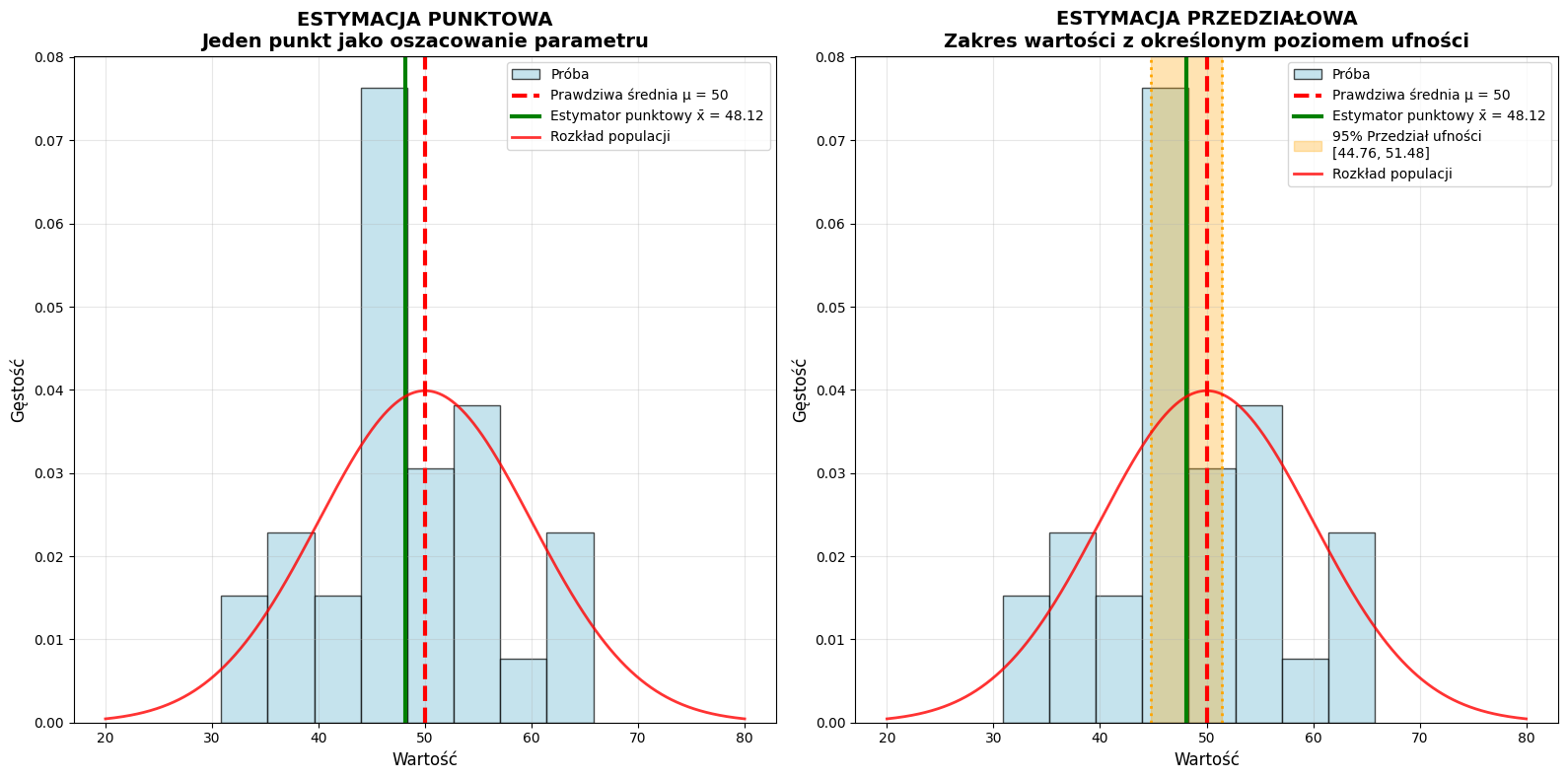

============================================================
PODSTAWOWE KONCEPCJE ESTYMACJI
============================================================

1. ESTYMACJA PUNKTOWA:
   • Jeden punkt jako oszacowanie parametru populacji
   • Przykład: x̄ = 48.12 jako estymator μ = 50

2. ESTYMACJA PRZEDZIAŁOWA:
   • Zakres wartości z określonym poziomem ufności
   • Przykład: 95% P.U. = [44.76, 51.48]

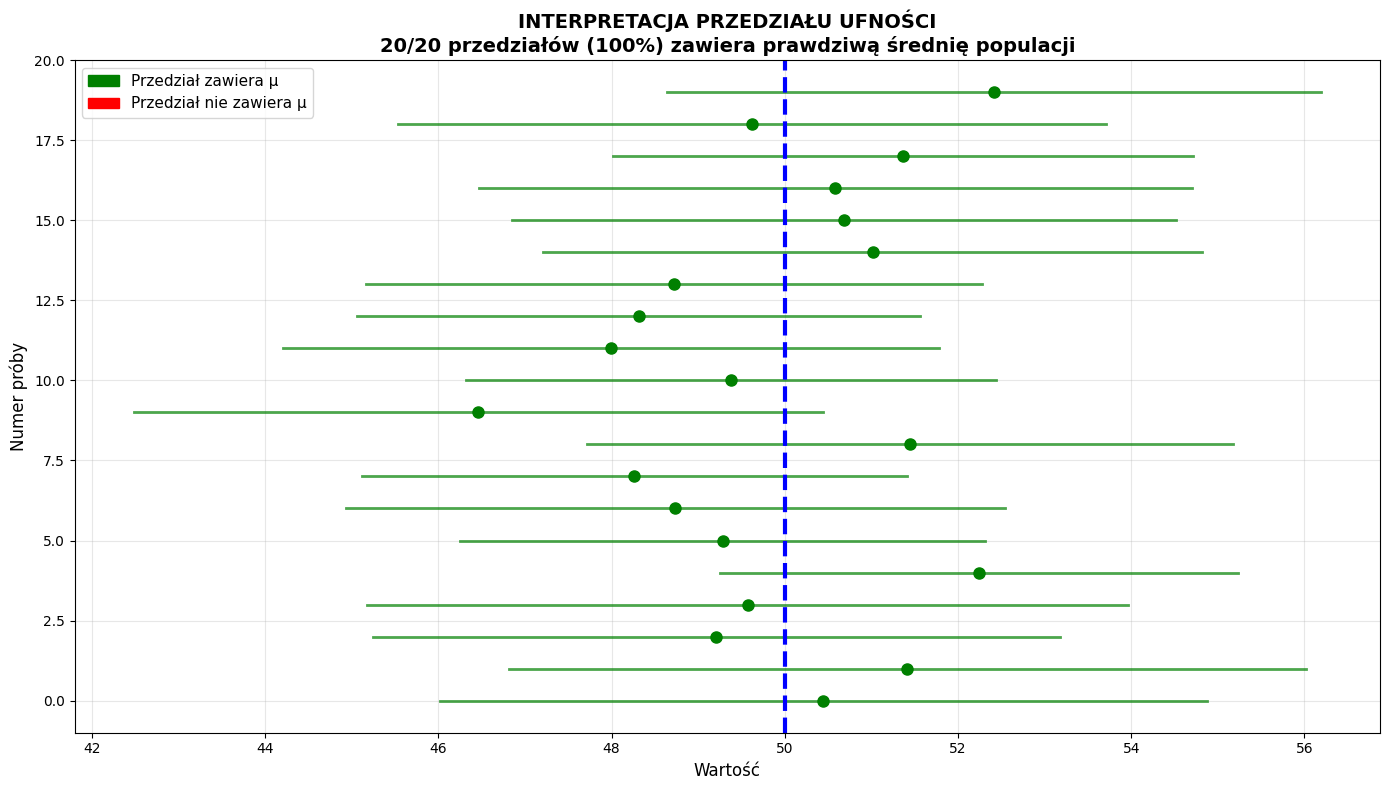
3. INTERPRETACJA PRZEDZIAŁU UFNOŚCI:
   • Jeśli powtórzymy procedurę 100 razy,
   • około 95 przedziałów będzie zawierało prawdziwą μ
   • W naszej symulacji: 100% przedziałów zawierało μ
============================================================

Zadanie 1.¶

Twoim zadaniem jest przeanalizowanie danych ankietowych dostępnych pod poniższym linkiem: surveydata3.csv. Analiza obejmuje oszacowanie średniej z przedziałami ufności, błędem standardowym, minimalną wielkością próby dla określonej dokładności oraz oszacowanie proporcji.

Dane są ładowane z pliku CSV dostępnego pod następującym linkiem: surveydata3.csv.
Zbiór danych zawiera 753 wiersze i 55 kolumn, w tym różne zmienne demograficzne i odpowiedzi ankietowe.
Szczegółowy opis zbioru danych można znaleźć tutaj.

Instrukcje

Załaduj dane:

Załaduj dane z pliku CSV.
Oblicz średnią liczbę godzin snu na dobę.
Oblicz odsetek osób, które chcą kupić gadżety Udacity.

Oszacowanie średniej:

Oblicz średnią liczby godzin snu na dobę studentów Udemy.
Oblicz przedział ufności dla średniej.
Oblicz błąd standardowy.
Oblicz minimalną wielkość próby wymaganą do osiągnięcia określonej dokładności (np. 3%).
Wizualizuj wyniki za pomocą wykresu pudełkowego (średnia, błędy standardowe, przedział ufności).

import pandas as pd
import matplotlib.pyplot as plt

url = 'https://raw.githubusercontent.com/juanspinzon/survey-data/refs/heads/main/clean_surveydata3.xlsx?raw=true'
df = pd.read_excel(url, engine='openpyxl')
dane = df["sleep hours per night"]
dane = dane.dropna()
print(dane.head())

plt.hist(dane,bins=10);

2    7.0
3    7.0
4    8.0
5    6.0
6    8.0
Name: sleep hours per night, dtype: float64

# twoje rozwiązanie tutaj

# Odkomentuj następującą linię, aby zobaczyć rozwiązanie:
# %load ./solutions/solution11.py

Estymacja wariancji¶

Dlaczego stosujemy rozkład chi-kwadrat (χ²) w estymacji wariancji?¶

Podstawowe wyjaśnienie¶

Rozkład chi-kwadrat pojawia się naturalnie przy estymacji wariancji z bardzo konkretnego powodu matematycznego. Oto proste wyjaśnienie:

1. Punkt wyjścia - rozkład normalny¶

Jeśli mamy próbkę z rozkładu normalnego:

X_1, X_2, \ldots, X_n \sim N(\mu, \sigma^2)

(1)

2. Standaryzacja obserwacji¶

Każdą obserwację możemy wystandaryzować:

Z_i = \frac{X_i - \mu}{\sigma} \sim N(0,1)

(2)

3. Suma kwadratów zmiennych standardowych¶

Gdy podnosimy do kwadratu i sumujemy standardowe zmienne normalne:

\sum_{i=1}^{n} Z_i^2 = \sum_{i=1}^{n} \left(\frac{X_i - \mu}{\sigma}\right)^2 \sim \chi^2(n)

(3)

To już jest rozkład chi-kwadrat z $n$ stopniami swobody.

4. Problem w praktyce - nieznana średnia¶

W praktyce nie znamy $\mu$ , więc używamy $\bar{X}$ :

\sum_{i=1}^{n} \left(\frac{X_i - \bar{X}}{\sigma}\right)^2

(4)

5. Kluczowe twierdzenie Fishera¶

Twierdzenie Fishera mówi, że:

\frac{\sum_{i=1}^{n}(X_i - \bar{X})^2}{\sigma^2} = \frac{(n-1)s^2}{\sigma^2} \sim \chi^2(n-1)

(5)

gdzie:

$s^2 = \frac{\sum_{i=1}^{n}(X_i - \bar{X})^2}{n-1}$ - wariancja próbkowa
Tracimy jeden stopień swobody przez szacowanie średniej

6. Dlaczego chi-kwadrat?¶

Chi-kwadrat powstaje, ponieważ:

Suma kwadratów: Wariancja to średnia z kwadratów odchyleń
Zmienne normalne: Zakładamy normalność populacji
Strata stopni swobody: Szacowanie średniej “kosztuje” jeden stopień swobody

Matematyczne uzasadnienie¶

Rozkład wariancji próbkowej:¶

\frac{(n-1)s^2}{\sigma^2} \sim \chi^2(n-1)

(6)

Gęstość chi-kwadrat:¶

f(x) = \frac{1}{2^{k/2}\Gamma(k/2)} x^{k/2-1} e^{-x/2}, \quad x \geq 0

(7)

gdzie $k = n-1$ to stopnie swobody.

Praktyczne konsekwencje¶

Przedział ufności dla wariancji:¶

P\left(\chi^2_{\alpha/2, n-1} \leq \frac{(n-1)s^2}{\sigma^2} \leq \chi^2_{1-\alpha/2, n-1}\right) = 1-\alpha

(8)

Przekształcając na $\sigma^2$ :¶

P\left(\frac{(n-1)s^2}{\chi^2_{1-\alpha/2, n-1}} \leq \sigma^2 \leq \frac{(n-1)s^2}{\chi^2_{\alpha/2, n-1}}\right) = 1-\alpha

(9)

Właściwości rozkładu chi-kwadrat¶

Wartości nieujemne: $\chi^2 \geq 0$ (wariancja nie może być ujemna)
Asymetria: Rozkład jest prawostronnie skośny
Wartość oczekiwana: $E[\chi^2_k] = k$
Wariancja: $\text{Var}[\chi^2_k] = 2k$

Warunki stosowania¶

Rozkład chi-kwadrat dla wariancji jest poprawny tylko gdy:

Populacja ma rozkład normalny
Obserwacje są niezależne
Próbka jest losowa

Intuicyjne wyjaśnienie¶

Wyobraź sobie, że:

Mierzysz odchylenia od średniej: $(X_i - \bar{X})$
Podnosisz je do kwadratu: $(X_i - \bar{X})^2$
Sumujesz wszystkie: $\sum(X_i - \bar{X})^2$

Ta suma kwadratów odchyleń, przeskalowana przez prawdziwą wariancję, ma rozkład chi-kwadrat. To naturalna konsekwencja matematyki rozkładu normalnego.

Porównanie z rozkładem t-Studenta¶

Parametr	Rozkład t	Rozkład χ²
Estymacja	Średnia $\mu$	Wariancja $\sigma^2$
Gdy σ² jest	Nieznana	Szacowana
Statystyka	$\frac{\bar{X}-\mu}{s/\sqrt{n}}$	$\frac{(n-1)s^2}{\sigma^2}$
Symetryczny	Tak	Nie (prawostronna skośność)
Zakres	$(-\infty, +\infty)$	$[0, +\infty)$

Kluczowe wnioski¶

Chi-kwadrat używamy dla wariancji, bo matematycznie tak wynika z teorii
Jedna średnia = jeden stopień swobody mniej
Tylko dla rozkładu normalnego!
Przedziały ufności są asymetryczne (w przeciwieństwie do średniej)

exec(open('est_war.py').read())

Zadanie 2.¶

Oszacowanie wariancji:

Oblicz wariancję i odchylenie std. liczby godzin snu na dobę studentów Udemy.
Oblicz 95% przedział ufności dla wariancji.

# twoje rozwiązanie tutaj

Estymacja proporcji¶

exec(open('est_prop.py').read())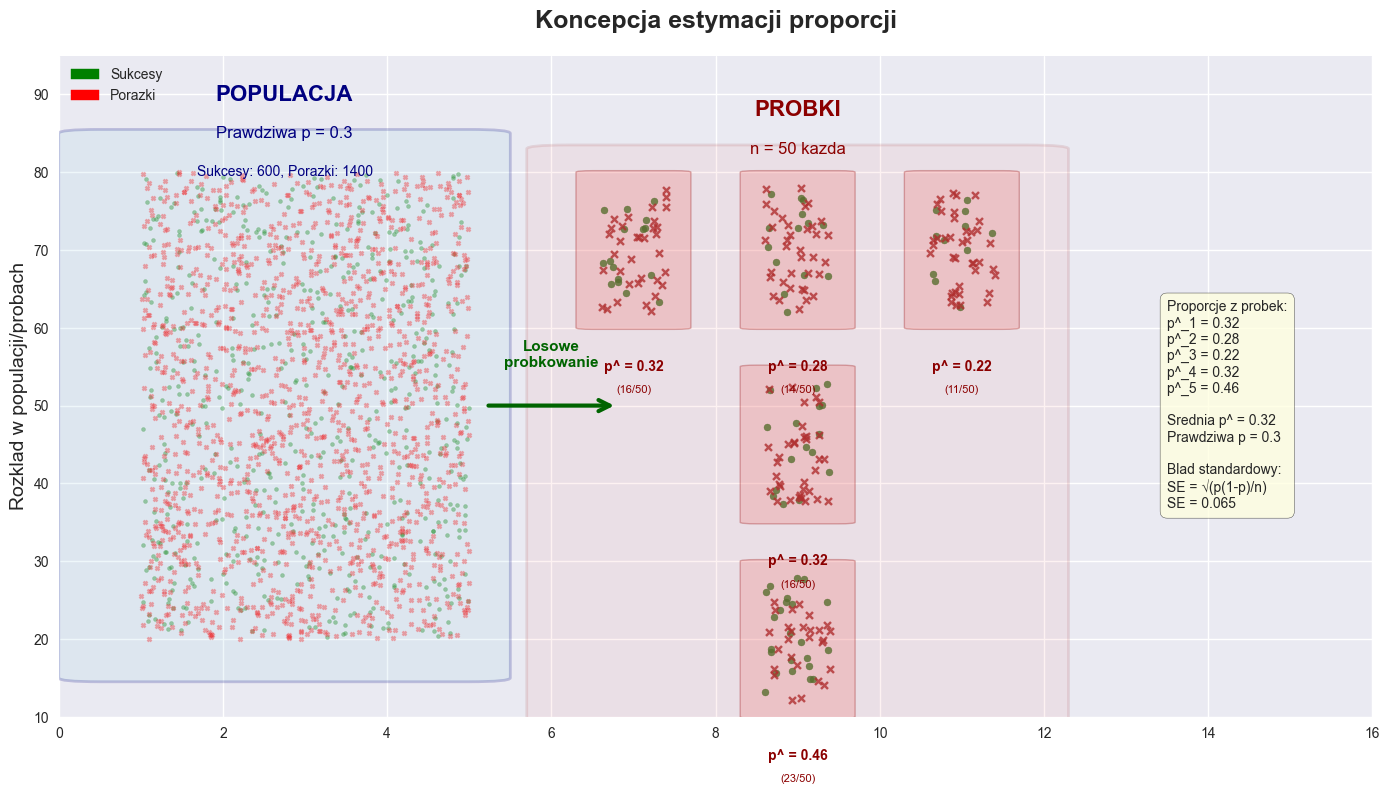

======================================================================
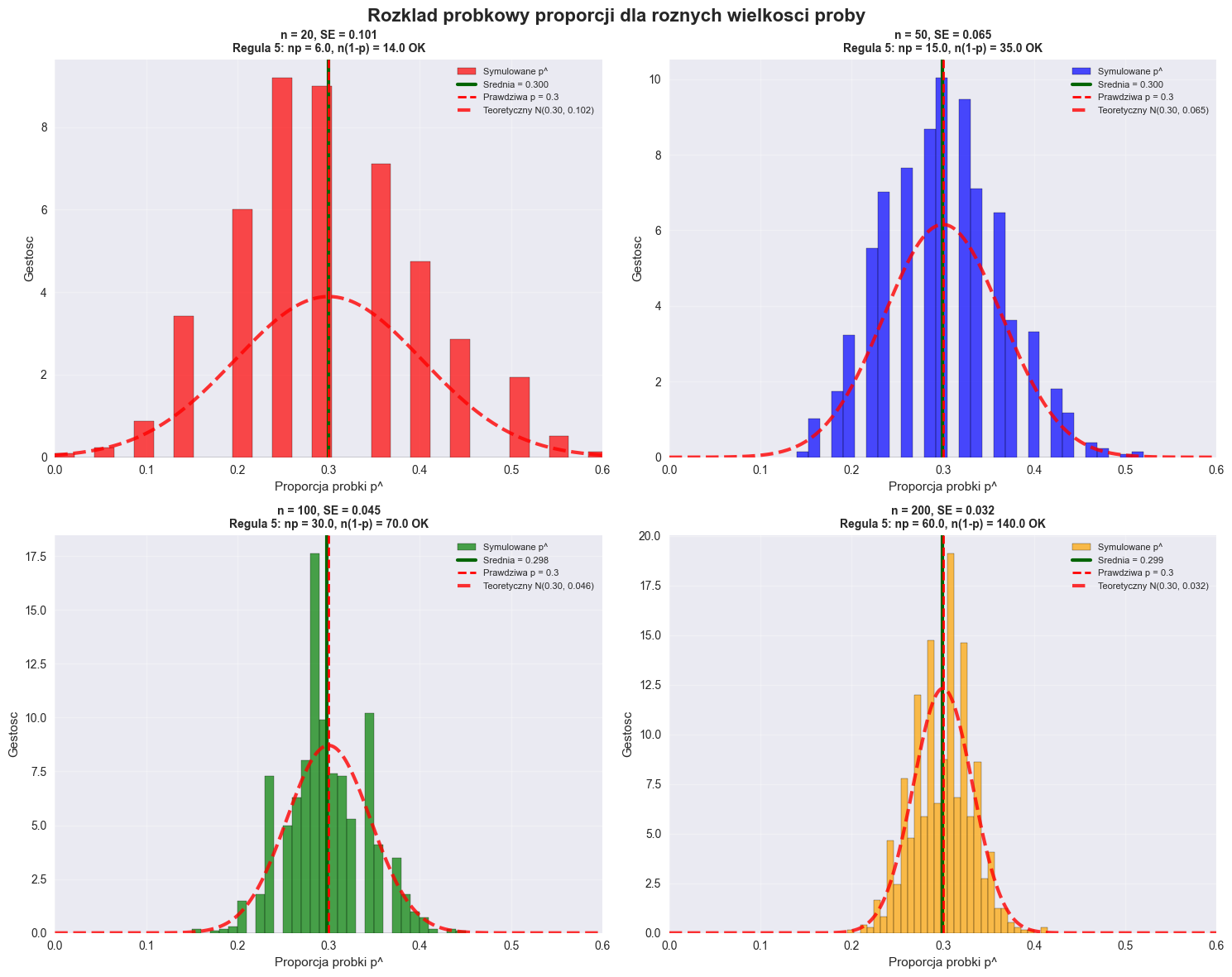
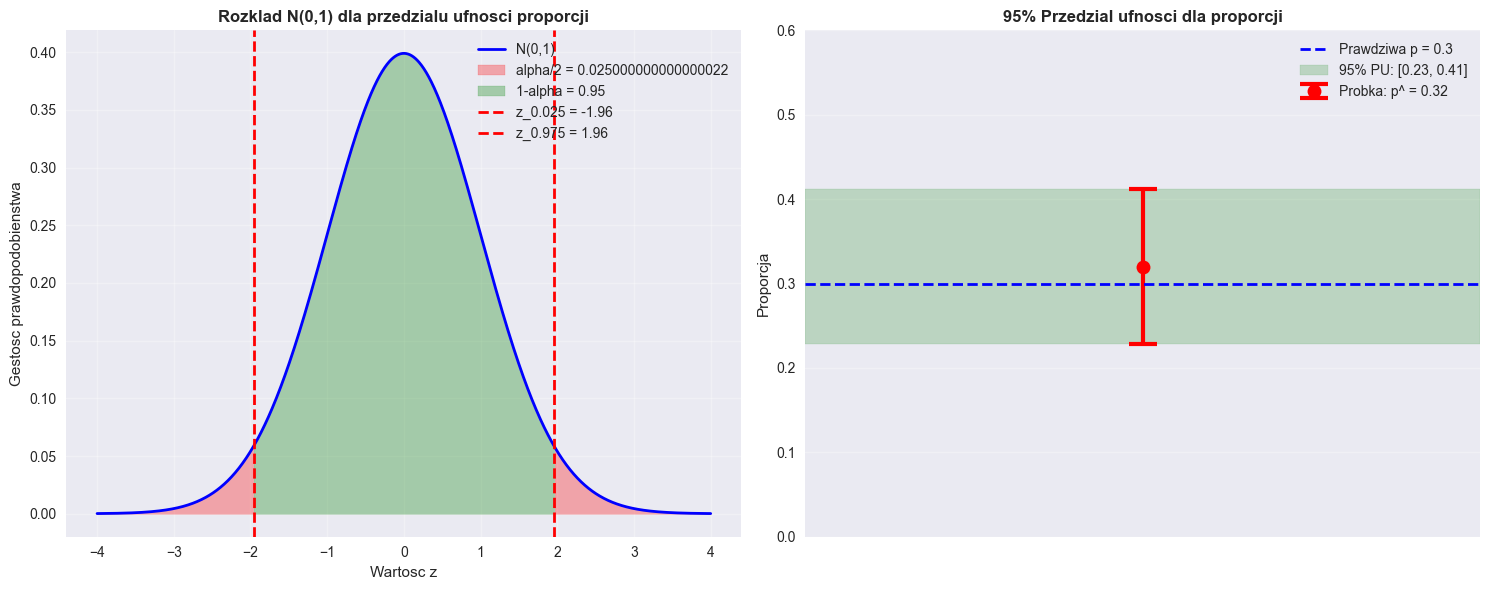
PODSUMOWANIE ESTYMACJI PROPORCJI
======================================================================
Prawdziwa proporcja populacji: p = 0.3
Wielkosc probki: n = 100

WYNIKI ESTYMACJI:
Liczba sukcesow: 32
Proporcja probkowa: p^ = 0.320
Blad standardowy: SE(p^) = 0.047
95% Przedzial ufnosci: [0.229, 0.411]
Margines bledu: ±0.091

SPRAWDZENIE REGULY 5:
np^ = 32.0 ≥ 5: TAK
n(1-p^) = 68.0 ≥ 5: TAK

WERYFIKACJA:
Czy przedzial zawiera prawdziwa wartosc? TAK
Szerokosc przedzialu: 0.183

Zadanie 3.¶

Oszacowanie proporcji:

Oblicz proporcję osób, które chcą kupić gadżety Udacity.
Oblicz przedział ufności dla tej proporcji.
Oblicz błąd standardowy.
Oblicz minimalną wielkość próby wymaganą do osiągnięcia określonej dokładności (np. 3%).
Wizualizuj wyniki za pomocą wykresu pudełkowego (proporcja, błędy standardowe, przedział ufności).

# twoje rozwiązanie tutaj

Zadanie domowe¶

Twoim zadaniem jest przeanalizowanie danych ankietowych “Diagnoza społeczna” przeprowadzanych przez wiele lat w Polsce.

Dane są ładowane z pliku CSV dostępnego w kategorii data/ankiety. W pliku “diagnozaDict.csv” znajdują się szczegółowe opisy pytań zadanych respondentom.