08 - Data preprocessing

W tym rozdziale¶

Data preprocessing (przetwarzanie wstępne danych) to etap przygotowania surowych danych do dalszej analizy, modelowania lub wizualizacji. Obejmuje on różne techniki i operacje, które mają na celu oczyszczenie (cleansing), uporządkowanie (tidying) i przekształcenie (wrangling) danych tak, aby były one spójne, kompletne i gotowe do użycia w narzędziach analitycznych lub algorytmach uczenia maszynowego.

Celem data preprocessingu jest uzyskanie wysokiej jakości zbioru danych, który pozwala na uzyskanie wiarygodnych i użytecznych wyników analizy.

W niedawnym artykule z New York Timesa napisano:

„Naukowcy zajmujący się danymi, według wywiadów i szacunków ekspertów, spędzają od 50 do 80 procent swojego czasu na przyziemnej pracy związanej z gromadzeniem i przygotowywaniem danych, zanim będzie można je zbadać pod kątem przydatnych informacji”.

Jak?

dostrzegać zmienne i obserwacje w danych
szybko uzyskiwać nowe zmienne i obserwacje do zbadania
przekształcać dane w układ, który najlepiej sprawdza się w Pythonie
łączyć ze sobą wiele zestawów danych
używać podsumowań grupowych do odkrywania ukrytych poziomów informacji w danych

Można by poświęcić temu cały kurs, ale dzisiaj skupimy się na tym:

Czym jest data wrangling?
Co zrobić z brakującymi wartościami?
Co zrobić z brudnymi danymi?
Jak łączyć zbiory danych?
Porządkowanie danych!
- Co to jest?
- Jak sprawić, by nasze dane były uporządkowane?

import seaborn as sns 
import pandas as pd
import numpy as np

%matplotlib inline 
%config InlineBackend.figure_format = 'retina'

Czym jest data wrangling?¶

Data wrangling odnosi się do manipulowania, reshapingu lub przekształcania zbioru danych w zależności od potrzeb (np. wizualizacji i/lub analizy).

Ogromna część pracy z danymi obejmuje „manipulowanie”.
Obejmuje to:
- „Czyszczenie” danych (brakujące wartości, przekształcanie zmiennych itp.).
- Scalanie/łączenie różnych zestawów danych.
- Przekształcanie danych w razie potrzeby.

Data Wrangling z Pandas¶

CHEAT-SHEET dostępny jest tutaj

Radzenie sobie z brakującymi wartościami¶

W praktyce, rzeczywiste dane są często nieuporządkowane.
Obejmuje to brakujące wartości, które przyjmują wartość/etykietę NaN.
- NaN = „Not a Number”.
Radzenie sobie z wartościami NaN jest jednym z głównych wyzwań w SAD!

Rodzaje braków danych¶

Zanim zaczniemy analizować brakujące wartości, ważne jest, aby zrozumieć różne przyczyny braku danych. Ogólnie rzecz biorąc, mogą istnieć trzy możliwe powody:

1. Brak całkowicie losowy (MCAR).

Brakujące wartości danej zmiennej (Y) nie są powiązane z innymi zmiennymi w danym zestawie danych lub z samą zmienną (Y). Innymi słowy, nie ma konkretnego powodu dla brakujących wartości.

2. Braki losowe (MAR).

MAR występuje, gdy brak nie jest losowy, ale gdy brak może być w pełni wyjaśniony przez zmienne, o których istnieją pełne informacje.

3. Braki nielosowe (MNAR).

Braki zależą od nieobserwowanych danych lub wartości samych brakujących danych.

MCAR¶

Co to oznacza? Gdy brakujące punkty danych nie są zgodne z żadnym konkretnym rozumowaniem lub wzorcem.

Przykład 1. Masz dane demograficzne mieszkańców swojej społeczności. Ale w zmiennej „Drugie imię” brakuje 50% wartości. Te 50% danych jest doskonałym przykładem MCAR danych. Nie ma wzorca ani konkretnego powodu, dla którego drugie imię jest puste w większości wpisów.
Przykład 2. W ankiecie papierowej jedna strona przypadkowo wypadła z kilku formularzy podczas transportu. Brakuje więc odpowiedzi na pytania ze strony 3, ale niezależnie od tego, kim był respondent czy jak odpowiadał wcześniej.

Jak sobie z tym poradzić?

W przypadku MCAR danych można zastosować następujące metody:

Usuwanie wierszami: Usunięcie rekordu, jeśli w zbiorze danych brakuje danych w którejkolwiek ze zmiennych/kolumn. Działa to najlepiej tylko wtedy, gdy liczba brakujących danych jest niewielka, na przykład gdy w zbiorze danych brakuje tylko 2% danych całkowicie losowo.
Usuwanie parami: Usuwanie parami usuwa tylko przypadki, w których brakuje jednej ze zmiennych używanych w rozważanej metodzie statystycznej. Działa na tej samej zasadzie co macierz korelacji. W przypadku brakujących wartości między dwiema zmiennymi (w sensie parami) znalezienie macierzy korelacji uwzględnia wszystkie pełne przypadki dla tych dwóch zmiennych. Załóżmy, że liczba przypadków w tym scenariuszu wynosi N. Po pobraniu innego zestawu zmiennych i obliczeniu macierzy korelacji liczba kompletnych przypadków będzie różnić się od N. Służy to jako główna różnica między usuwaniem wierszami i parami. Usuwanie parami ma tę zaletę, że powoduje minimalną utratę danych. W przypadku zbioru danych, który ma powszechne brakujące wartości w prawie wszystkich zmiennych, usuwanie parami byłoby mądrzejszym wyborem radzenia sobie z brakującymi wartościami.
Średnia, mediana i imputacja trybu: Brakujące wartości można również zastąpić średnią, medianą i modą odpowiednich zmiennych.

MAR¶

Co to oznacza? Gdy brakujące punkty danych podążają za wzorcem.

Przykład 1. Weźmy ten sam przykład danych demograficznych mieszkańców Twojej społeczności. Ale tym razem brakuje wynagrodzenia kilku mężczyzn w wieku powyżej 45 lat.
Przykład 2. W badaniu zdrowotnym kobiety częściej niż mężczyźni nie podają swojej wagi. Brak danych zależy od płci (która jest znana), ale nie od samej wartości wagi.

W tym przypadku brak danych jest przypisany do danych innej zmiennej. W związku z tym jest to mechanizm „missing at random”. MAR jest prawdopodobnie najtrudniejszy do zrozumienia ze względu na swoją nazwę.

Jak sobie z nim radzić?

Ponieważ w tym mechanizmie występuje związek, najlepszą opcją byłoby zastosowanie techniki imputacji - średniej, mediany, trybu lub wielokrotnej imputacji.

MNAR¶

Co to oznacza?

Gdy brakujące punkty danych są zgodne z wzorcem, oznacza to, że są one zgodne z mechanizmem MNAR.

Przykład 1. W tych samych danych demograficznych mieszkańców Twojej społeczności, powiedzmy, że brakuje wynagrodzenia kilku mężczyzn, gdy wynagrodzenie przekracza określoną kwotę. (powiedzmy milion).
Przykład 2. Osoby z bardzo wysokimi dochodami nie chcą ujawniać swoich zarobków w ankiecie. Brak danych o dochodzie zależy bezpośrednio od jego wartości (czyli tej, której właśnie brakuje).

W tym przypadku mamy do czynienia z mechanizmem „Missing Not at Random”. Zazwyczaj, gdy brakujące dane nie są MCAR lub MAR, mają tendencję do naśladowania MNAR.

Jak sobie z tym poradzić?

Ponieważ w przypadku MNAR występuje zależność indukowana przez samą siebie, najlepszym sposobem na uniknięcie jej jest gromadzenie danych lub modelowanie brakujących danych.

Powodem, dla którego musimy przeanalizować mechanizmy brakujących wartości, jest to, że musimy zrozumieć najlepszy sposób na przypisanie brakującej wartości, aby dokładność naszych modeli ML pozostała bez wpływu.

Ładowanie zbioru danych z brakującymi wartościami¶

Zbiór danych titanic zawiera informacje o różnych pasażerach Titanica i o tym, czy przeżyli (1 vs. 0).

Powszechnie używany jako samouczek do uczenia maszynowego, regresji i zarządzania danymi.

df_titanic = pd.read_csv("data/wrangling/titanic.csv")
df_titanic.head(3)

Dlaczego brakujące dane stanowią problem?¶

Jeśli nie jesteśmy świadomi brakujących danych:

Możemy przeszacować rozmiar swojego zbioru danych.
Możemy obciążyć wyniki wizualizacji lub analizy (jeśli brakujące dane są rozłożone nielosowo).
Możemy skomplikować analizę.
- Domyślnie wiele pakietów analitycznych „porzuca” brakujące dane - więc musimy być świadomi, czy tak się dzieje.

Jak radzić sobie z brakującymi danymi¶

Zidentyfikuj, czy i gdzie dane mają brakujące wartości.
Zanalizuj jak te brakujące wartości są rozłożone.
Zdecyduj jak sobie z nimi poradzić.

Nie jest to łatwy problem - zwłaszcza krok 3!

Krok 1: Identyfikacja brakujących wartości¶

Pierwszym krokiem jest identyfikacja, czy i gdzie w danych występują brakujące wartości.

Istnieje do tego kilka podejść:

Użycie .isna
Użycie .info
Użycie .isnull

`isna()`¶

Funkcja isna() mówi nam, czy dana komórka w DataFrame ma brakującą wartość czy nie (True vs False).
Jeśli wywołamy funkcję isna().any(), powie nam ona, które kolumny mają brakujące wartości.

df_titanic.isna().head(1)

df_titanic.isna().any()

Sprawdzanie kolumn z `nan`¶

Teraz możemy sprawdzić konkretne kolumny, które mają wartości nan.

df_titanic[df_titanic['Age'].isna()].head(5)

Ile `nan`?¶

Jeśli wywołamy sum na wartościach nan, możemy dokładnie obliczyć ile wartości nan znajduje się w każdej kolumnie.

df_titanic.isna().sum()

`info`¶

Funkcja info() daje nam różne informacje na temat DataFrame, włączając w to liczbę nie-null (tj. nie brakujących) wartości w każdej kolumnie.

df_titanic.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 891 entries, 0 to 890
Data columns (total 12 columns):
 #   Column       Non-Null Count  Dtype  
---  ------       --------------  -----  
 0   PassengerId  891 non-null    int64  
 1   Survived     891 non-null    int64  
 2   Pclass       891 non-null    int64  
 3   Name         891 non-null    object 
 4   Sex          891 non-null    object 
 5   Age          714 non-null    float64
 6   SibSp        891 non-null    int64  
 7   Parch        891 non-null    int64  
 8   Ticket       891 non-null    object 
 9   Fare         891 non-null    float64
 10  Cabin        204 non-null    object 
 11  Embarked     889 non-null    object 
dtypes: float64(2), int64(5), object(5)
memory usage: 83.7+ KB

Twoja kolej!¶

W ilu wierszach DataFrame brakuje wartości dla Cabin?

### Twój kod tutaj
df_titanic[['Cabin']].isna().sum()

Wizualizacja brakujących wartości¶

Wreszcie, możemy zwizualizować wskaźnik brakujących wartości w kolumnach za pomocą seaborn.heatmap.
- Ciemne komórki to te z wartościami niezerowymi.
- Jasne komórki mają wartości nan.

sns.heatmap(df_titanic.isna());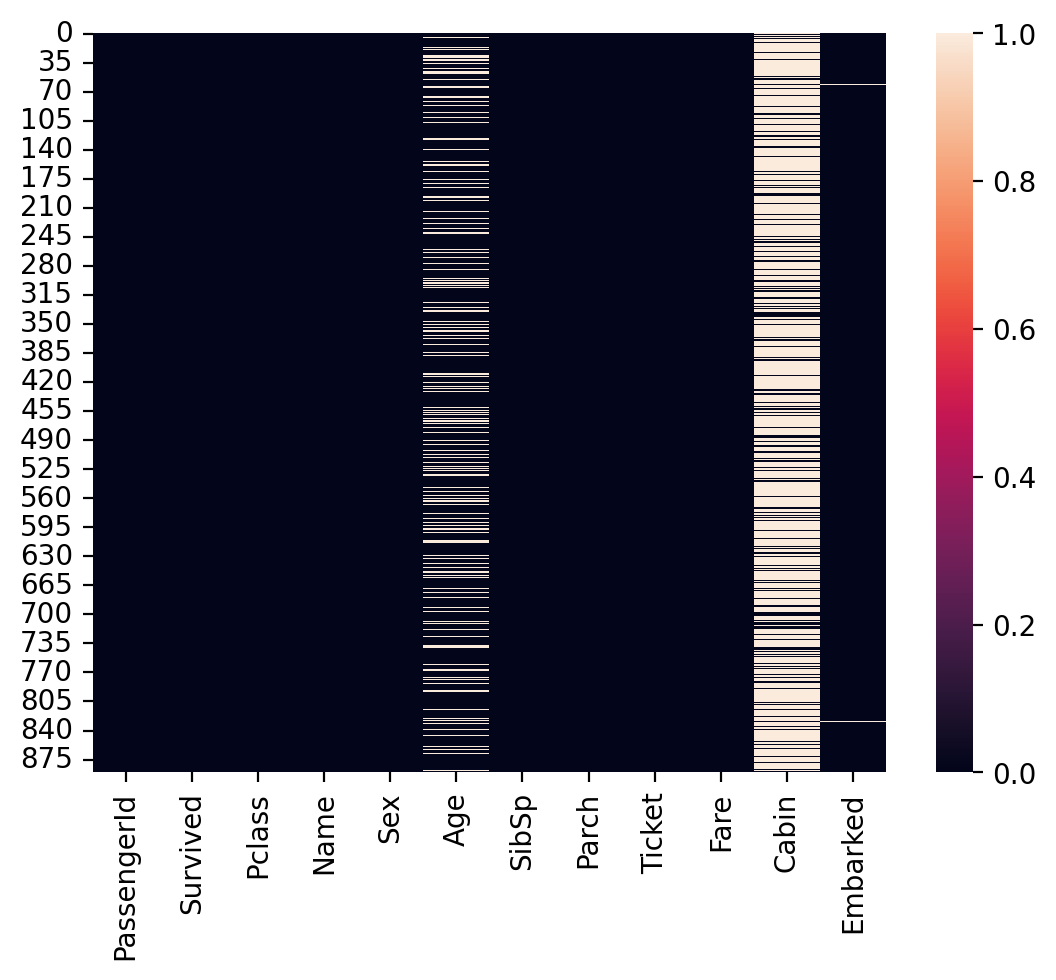

Krok 2: Analiza rozkładu danych¶

Po zidentyfikowaniu brakujących danych, następnym krokiem jest określenie, w jaki sposób te brakujące dane są rozłożone.

Czy zmienna $Y$ jest różna w zależności od tego, czy $X$ jest `nan`?¶

Jednym z podejść jest zapytanie, czy jakaś zmienna będąca przedmiotem zainteresowania (np. Przeżył) jest różna w zależności od tego, czy jakaś inna zmienna jest nan.

### Średnie przeżycie dla osób bez danych dotyczących informacji o kabinie
df_titanic[df_titanic['Cabin'].isna()]['Survived'].mean()

np.float64(0.29985443959243085)

### Średnie przeżycie dla osób *posiadających* dane dotyczące informacji o kabinie
df_titanic[~df_titanic['Cabin'].isna()]['Survived'].mean()

np.float64(0.6666666666666666)

Twoja kolej!¶

Jaki jest średni wskaźnik Survived dla wartości z wartością nan dla Age w porównaniu do tych z wartościami non-null? Jak wypada to w porównaniu z ogólnym wskaźnikiem Survived?

### Twój kod tutaj

Pakiet `missingno`¶

Jeśli chcesz zagłębić się w temat, możesz zapoznać się z biblioteką missingno w Pythonie (którą należy zainstalować osobno).

Znalezienie przyczyny braku danych przy użyciu wykresu macierzowego¶

import missingno as msno
msno.matrix(df_titanic);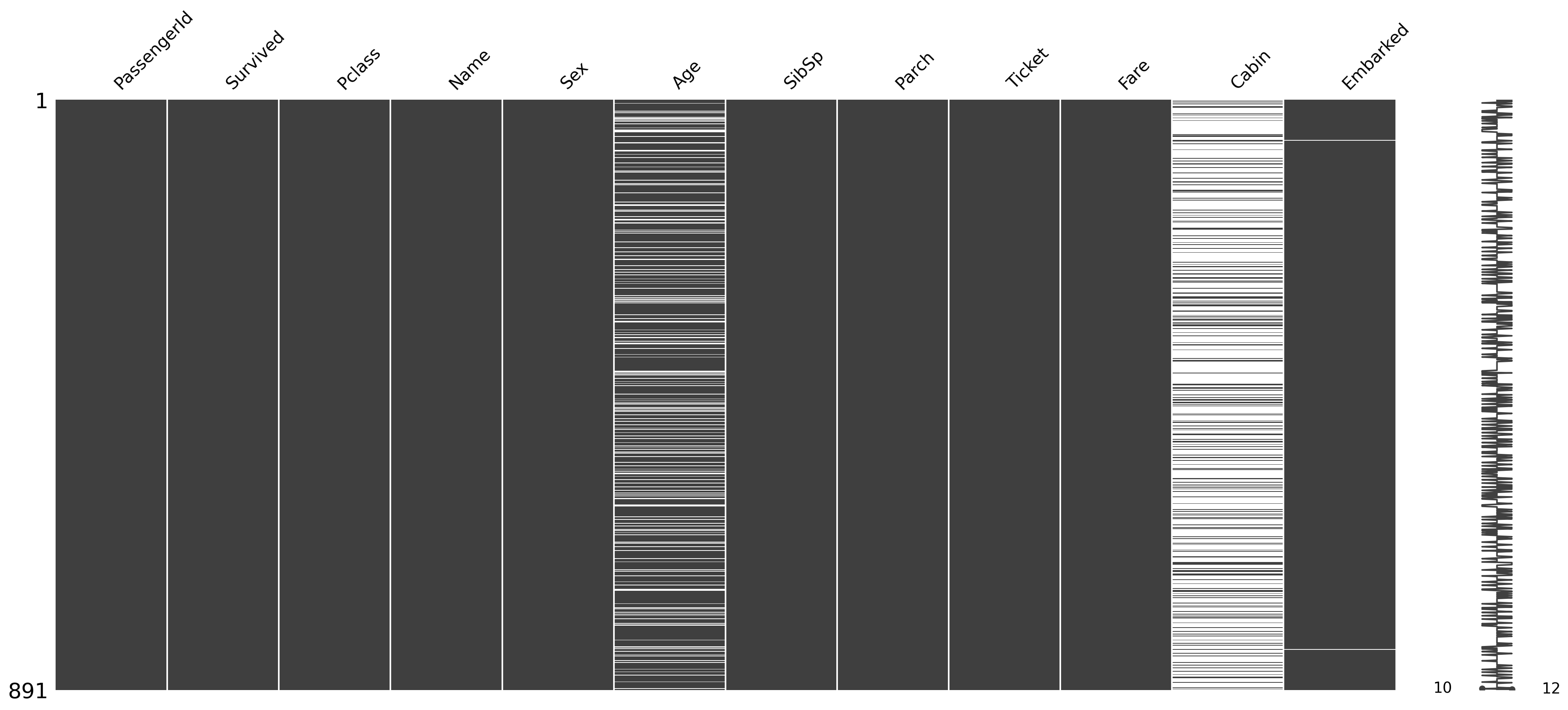

Znalezienie przyczyny brakujących danych przy użyciu Heatmapy¶

msno.heatmap(df_titanic);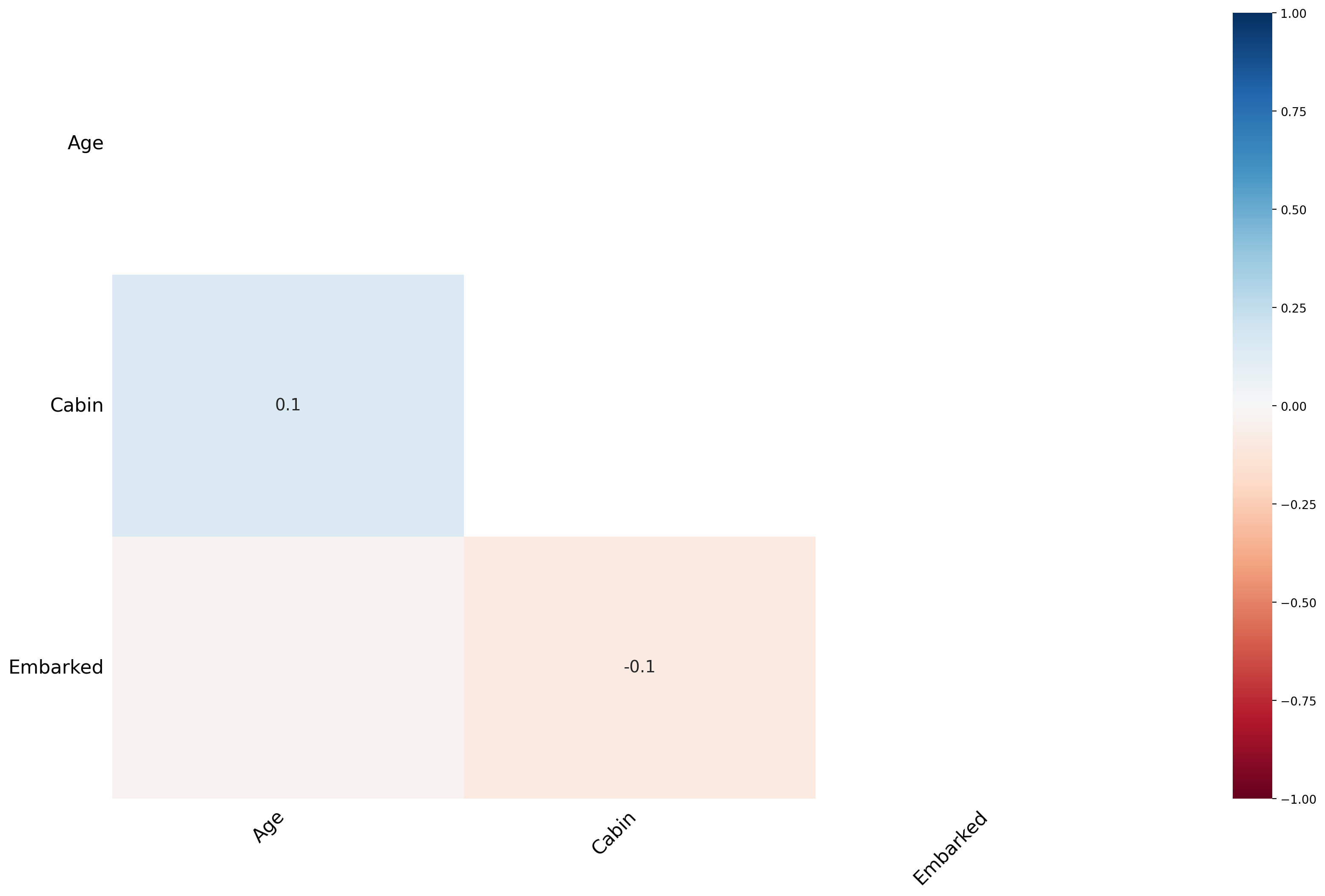

Funkcja mapy cieplnej pokazuje, że nie ma silnych korelacji między brakującymi wartościami różnych cech. To dobrze; niskie korelacje wskazują ponadto, że dane są MAR.

Znajdowanie przyczyny braku danych przy użyciu dendrogramu¶

Dendrogram to diagram drzewa brakujących danych. Grupuje on razem wysoce skorelowane zmienne.

Jak następuje podział na drzewie?

Metoda Warda to jedna z metod hierarchicznego grupowania (ang. hierarchical clustering), używana m.in. w msno.dendrogram. Działa ona w następujący sposób:

Na początku każda kolumna (lub obserwacja) traktowana jest jako osobna grupa.
Na każdym kroku łączone są te dwie grupy, których połączenie powoduje najmniejszy wzrost tzw. sumy kwadratów odchyleń wewnątrzgrupowych (ang. within-cluster sum of squares).
Celem jest minimalizacja wzrostu “błędu” po połączeniu – czyli łączone są te grupy, które są do siebie najbardziej podobne pod względem rozkładu braków.
Proces powtarza się aż do połączenia wszystkich grup w jedno drzewo (dendrogram).

W praktyce: Metoda Warda tworzy najbardziej “kompaktowe” i jednorodne grupy, minimalizując różnice wewnątrz każdej grupy na każdym etapie łączenia.

msno.dendrogram(df_titanic);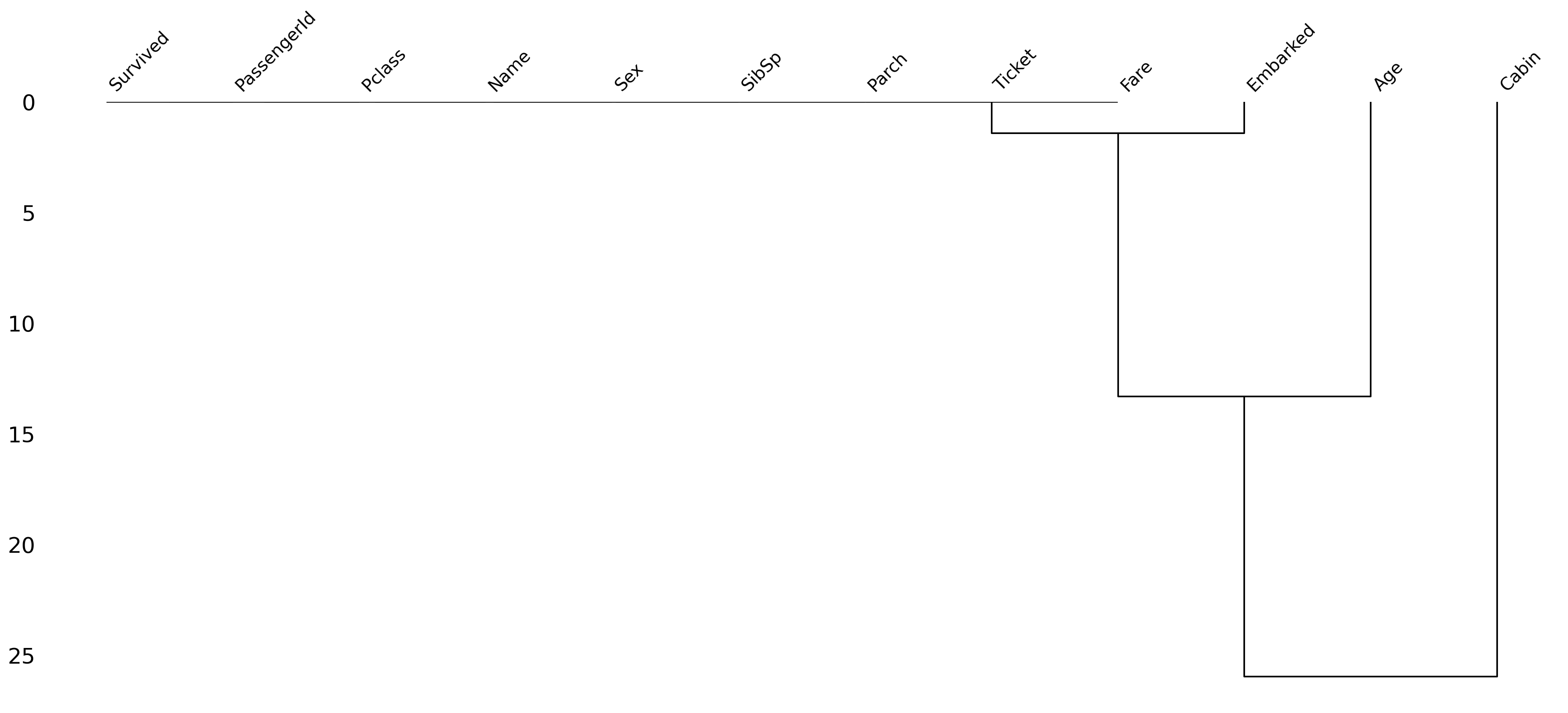

Jak czytać dendrogram?

Przeczytajmy powyższy dendrogram z góry na dół:

Im niższy poziom połączenia (bliżej zera na osi Y), tym silniejsza zależność – np. kolumny zawsze mają braki w tych samych wierszach. Wysokość połączenia (na osi Y) pokazuje, jak bardzo różnią się wzorce braków między grupami kolumn – im wyżej, tym mniej podobne. Bliskie połączenie (nisko) oznacza, że braki w tych kolumnach są silnie skorelowane. Oddalone połączenie (wysoko) oznacza, że braki występują niezależnie.

Liście klastra, które łączą się ze sobą w odległości równej zero, w pełni przewidują wzajemną obecność - jedna zmienna może być zawsze pusta, gdy inna jest wypełniona, lub obie mogą być zawsze wypełnione lub obie puste i tak dalej.

Jednak w tym konkretnym przypadku korelacja jest wysoka, ponieważ kolumna Embarked ma bardzo niewiele brakujących wartości. Ten zbiór danych nie ma zbyt wielu brakujących wartości, ale jeśli zastosujesz tę samą metodologię do zbiorów danych zawierających wiele brakujących wartości, z pewnością pojawi się jakiś interesujący wzorzec.

Podsumowując:

Jeśli dwie kolumny łączą się bardzo nisko, to prawie zawsze mają braki w tych samych wierszach.
Jeśli kolumna łączy się z innymi dopiero wysoko, jej braki są raczej niezależne.

Dendrogram pomaga znaleźć grupy zmiennych, które mają podobny rozkład braków – to ważne np. przy imputacji lub analizie przyczyn braków.

Krok 3: Ustal, co należy zrobić!¶

Po zidentyfikowaniu brakujących danych należy określić, w jaki sposób je obsłużyć.

Istnieje kilka możliwych podejść.

Usunięcie wszystkich wierszy z wszystkimi brakującymi danymi.
Usuwanie wierszy z brakującymi danymi tylko wtedy, gdy zmienna ta jest istotna dla analizy lub wizualizacji.
Imputowanie (tj. zgadywanie), jakie wartości powinny mieć brakujące dane.

Usuwanie wszystkich wierszy z brakującymi danymi¶

Możemy filtrować naszą DataFrame używając dropna, która automatycznie „usunie” wszystkie wiersze zawierające wartości null.
Uwaga: jeśli masz wiele brakujących danych, może to znacząco wpłynąć na rozmiar twojego zbioru danych.

df_filtered = df_titanic.dropna()
df_filtered.shape

(183, 12)

Usuwanie wszystkich wierszy z brakującymi danymi w określonych kolumnach¶

Tutaj określamy, że chcemy tylko dropna dla wierszy, które mają nan w kolumnie Age.
Nadal mamy brakujące nan dla Cabin, ale być może w naszym przypadku jest to w porządku.

df_filtered = df_titanic.dropna(subset = "Age")
df_filtered.shape

(714, 12)

Imputowanie brakujących danych¶

Jednym z najbardziej złożonych (i kontrowersyjnych) podejść jest imputowanie wartości brakujących danych.

Istnieje (ponownie) wiele sposobów, aby to zrobić:

Ustalenie stałej wartości i przypisanie jej do wszystkich wartości nan.
- Na przykład, przypisz średni wiek wszystkim osobom z nan w tej kolumnie.
Spróbuj odgadnąć wartość na podstawie określonych cech danych.
- Np. na podstawie innych cech tej osoby, jaki jest jej prawdopodobny wiek?

Imputowanie stałej wartości¶

Możemy użyć fillna, aby przypisać wszystkim wartościom z nan dla Age jakąś inną wartość.

## Przypisz średni wiek do wszystkich osób z nan dla wieku
df_titanic['Age_imputed1'] = df_titanic['Age'].fillna(df_titanic['Age'].mean())
## Przyjrzyjmy się teraz tym wierszom
df_titanic[df_titanic['Age'].isna()].head(5)

Zgadywanie na podstawie innych cech¶

Możesz spróbować zgadnąć jaki byłby ich Age, bazując na innych cechach.
Bardziej wyrafinowaną wersją tego jest użycie modelowania statystycznego lub użycie SimpleImputer z biblioteki sklearn.
Na razie wystarczy zauważyć, że Age koreluje z innymi cechami (takimi jak Pclass).

## Klasa pasażerów jest skorelowana z wiekiem
sns.barplot(data = df_titanic, x = 'Pclass', y = 'Age');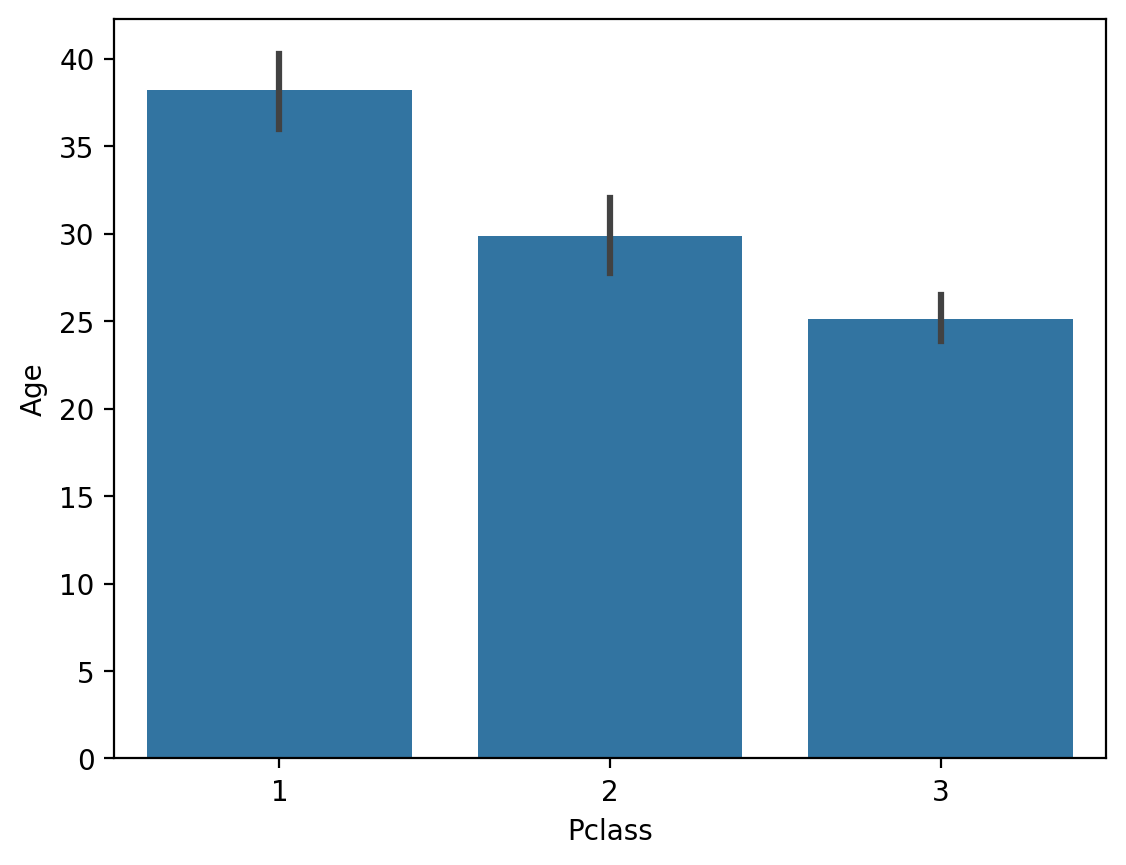

Twoja kolej!¶

Co by się stało, gdybyśmy użyli fillna z median Age zamiast mean? Dlaczego miałoby to znaczenie?

### Twój kod tutaj

Imputacja losowa / hot deck¶

Imputacja Hot Deck to metoda, w której każda brakująca wartość jest zastępowana wartością z podobnego rekordu w zbiorze danych, często określanego jako „dawca”. Rekord dawcy jest wybierany na podstawie kryteriów dopasowania - takich jak cechy demograficzne lub bliskość w wielowymiarowej przestrzeni cech - w celu zapewnienia, że imputacja zachowuje nieodłączny rozkład i relacje w danych.

Na przykład, jeśli brakuje danych o dochodach respondenta ankiety, wartość dochodu podobnego respondenta (oparta na czynnikach takich jak zawód, lokalizacja geograficzna i poziom wykształcenia) jest używana jako substytut.

Imputacja Hot Deck ma kluczowe znaczenie dla zachowania integralności zbioru danych. Zapewnia ona, że:

Analizy statystyczne nie są stronnicze z powodu arbitralnego lub odrzucenia niekompletnych przypadków.
Naturalna zmienność i wzorce dystrybucji obecne w kompletnych przypadkach są zachowane.
Porównania między różnymi grupami w ramach danych pozostają wykonalne i ważne.

Imputacja losowa Hot Deck: W tej metodzie brakujące wartości są imputowane poprzez losowy wybór dawcy z puli potencjalnych kandydatów. Pozwala to zachować rozkład danych, zwłaszcza gdy braki są losowe. Wadą jest jednak to, że losowość może przeoczyć niuanse w danych.

Imputacja Hot Deck najbliższego sąsiedztwa: W tym przypadku dawca jest wybierany na podstawie podobieństwa obserwowanych cech. Powszechnie stosowanym algorytmem jest podejście k-najbliższych sąsiadów (k-NN), które oblicza metrykę odległości między obserwacjami. Dla rekordu z brakującą wartością określa się jego k najbliższych sąsiadów (pod względem odległości euklidesowej lub Mahalanobisa), a jedna z ich wartości jest używana do imputacji.

Algorytm k-NN identyfikuje najbliższe rekordy, które minimalizują odległość:

$d(x, y) = \sqrt{\sum_{i=1}^n (x_i - y_i)^2}$

gdzie:

$(x)$ i $(y)$ to dwa punkty w przestrzeni n-wymiarowej,
$(x_i)$ i $(y_i)$ to współrzędne punktów $(x)$ i $(y)$ w wymiarze $(i)$ ,
$d(x, y)$ to odległość euklidesowa między punktami $(x)$ i $(y)$ .

Imputacja Hot Deck oferuje kilka korzyści w porównaniu z innymi metodami:

Imputacja średniej/mediany: W przeciwieństwie do zwykłego zastępowania brakujących wartości ogólną średnią lub medianą, imputacja Hot Deck wykorzystuje informacje z podobnych przypadków. Pozwala to zachować lokalną zmienność i uwzględnia relacje między zmiennymi.
Imputacja regresyjna: Podczas gdy imputacja regresji opiera się na modelach predykcyjnych w celu oszacowania brakujących wartości, może ona prowadzić do stronniczych szacunków, jeśli założenia modelu zostaną naruszone. Natomiast imputacja Hot Deck bezpośrednio zapożycza obserwowane wartości, często czyniąc ją bardziej odporną w różnych warunkach.
Imputacja wielokrotna: Imputacja wielokrotna tworzy kilka imputowanych zestawów danych i łączy wyniki do ostatecznej analizy, uwzględniając niepewność imputacji. Chociaż często jest bardziej wyrafinowana statystycznie, może być kosztowna obliczeniowo. Imputacja Hot Deck pozostaje praktycznym wyborem, gdy priorytetem jest zachowanie łatwości interpretacji i wydajności obliczeniowej.

Głównym wnioskiem jest to, że imputacja Hot Deck oferuje intuicyjne, praktycznie wykonalne podejście, które nadal respektuje statystyczne właściwości danych.

Imputacja losowa Hot-deck¶

# Przykład imputacji losowej Hot Deck
def random_hot_deck_imputation(df, column):
    # Filtrujemy wartości nie-null
    non_null_values = df[column].dropna().values
    # Zastępujemy NaN losową wartością z istniejących
    df[column] = df[column].apply(lambda x: np.random.choice(non_null_values) if pd.isna(x) else x)
    return df

# Imputacja dla kolumny 'Age'
df_titanic = random_hot_deck_imputation(df_titanic, 'Age')
df_titanic.isna().any()

Wybór optymalnej liczby sąsiadów w metodzie k-NN - metoda łokcia¶

Zamiast zgadywać i arbitralnie wybierać liczbę sąsiadów w metodzie imputacji k-NN - lepiej jest zastosować metodę łokcia (elbow method) do wyboru optymalnej liczby sąsiadów w imputacji k-NN (KNNImputer).

Metoda polega na:

Sztucznym usunięciu części znanych wartości w danych (np. losowo zamieniasz część wartości na NaN).
Imputacji braków dla różnych wartości n_neighbors (np. od 2 do 15).
Obliczeniu błędu (np. MSE) między wartościami imputowanymi a prawdziwymi.
Wizualizacji błędu w funkcji liczby sąsiadów – szukasz „łokcia”, czyli punktu, po którym dalsze zwiększanie liczby sąsiadów nie poprawia już znacząco wyniku.

Przykład kodu (nie jest to jeszcze prawdziwa imputacja istniejących braków, lecz sztuczne ich wytworzenie, aby zasymulować dobór optymalnej liczby k - sąsiadów):

from sklearn.impute import KNNImputer
from sklearn.metrics import mean_squared_error
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')

# Załóżmy, że masz df z kolumną 'Age' bez braków
df = df_titanic[['Age', 'Fare']].dropna().copy()
np.random.seed(42)
mask = np.random.rand(len(df)) < 0.2  # 20% losowych braków
df_missing = df.copy()
df_missing.loc[mask, 'Age'] = np.nan

errors = []
neighbors = range(2, 16)
for k in neighbors:
    imputer = KNNImputer(n_neighbors=k)
    imputed = imputer.fit_transform(df_missing)
    mse = mean_squared_error(df['Age'][mask], imputed[mask, 0])
    errors.append(mse)

plt.plot(neighbors, errors, marker='o')
plt.xlabel('Liczba sąsiadów (k)')
plt.ylabel('MSE')
plt.title('Elbow method dla KNNImputer')
plt.show()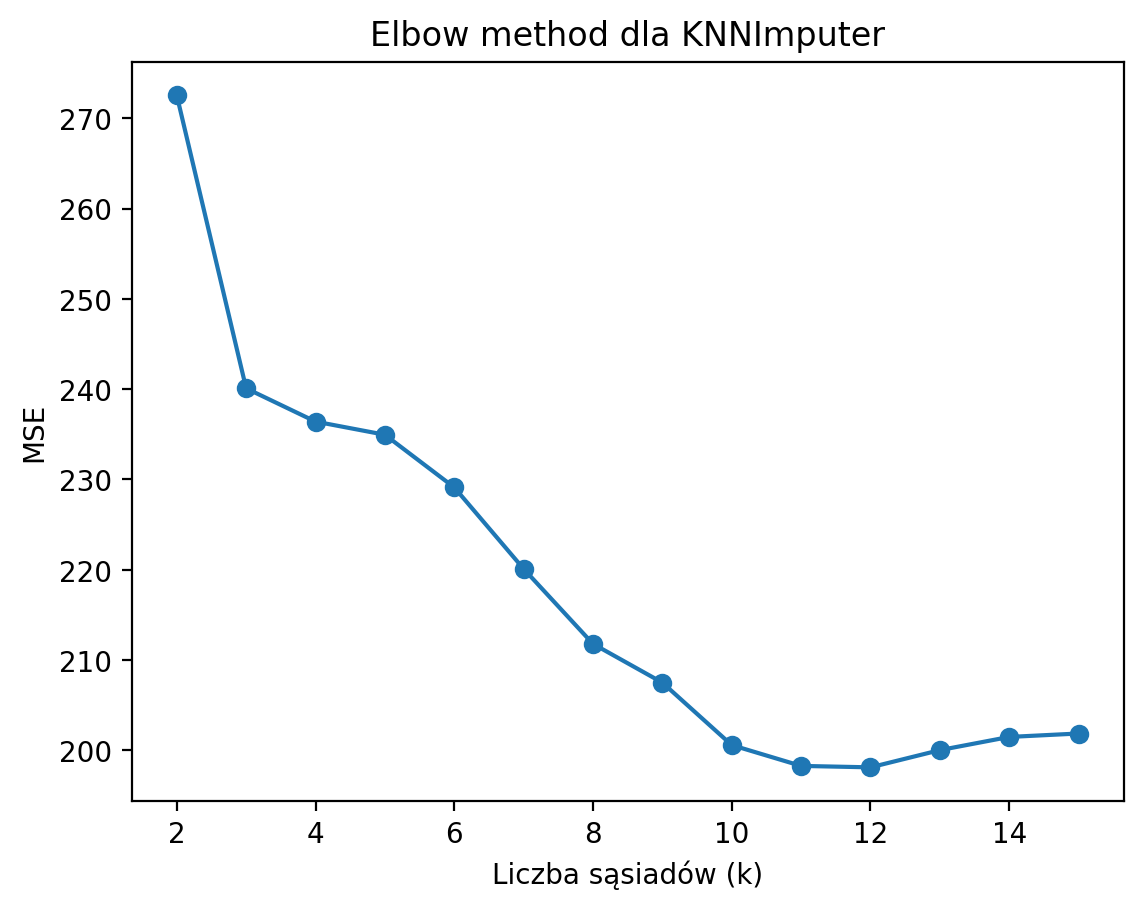

Wybieramy taką liczbę sąsiadów, gdzie błąd przestaje wyraźnie spadać – to jest „łokieć”.

Jak widzimy na wykresie, błąd MSE powoli maleje wraz ze wzrostem liczby sąsiadów, ale tempo spadku jest coraz mniejsze. W praktyce wybieramy taką wartość k, gdzie spadek błędu wyraźnie zwalnia (czyli „łokieć” wykresu). W naszym przypadku są to okolice k = 3–5 sąsiadów. Jeśli zależy nam na minimalnym błędzie, możemy wybrać większe k (np. 5 lub 6), ale zbyt duża liczba sąsiadów może prowadzić do nadmiernego uśredniania i utraty lokalnych zależności!

Najczęściej wybiera się k = 3 – to kompromis między błędem a zachowaniem struktury danych.

Podsumowanie:

k = 3 – klasyczny wybór, zgodny z „łokciem”
k = 5 – jeśli chcemy jeszcze minimalnie niższy błąd (ale różnica jest już niewielka)

Warto też sprawdzić, czy wyniki imputacji dla k = 3 i k = 5 są istotnie różne w naszych imputacjach.

Wybór optymalnej liczby sąsiadów w metodzie k-NN - metoda Silhouette¶

Inną niz metoda łokcia jest metoda Silhouette. Jest to narzędzie służące do oceny jakości klasteryzacji, które można również wykorzystać do wyboru optymalnej liczby sąsiadów (k) w imputacji brakujących danych za pomocą algorytmu k-NN (KNNImputer).

Nazwa “silhouette score” (po polsku: współczynnik sylwetki) pochodzi od angielskiego słowa silhouette, czyli „sylwetka”. Wskaźnik ten został wprowadzony przez Petera J. Rousseeuwa w 1987 roku jako miara jakości klasteryzacji.

Współczynnik ten mierzy, jak bardzo dana obserwacja jest podobna do własnego klastra (grupy), a jak bardzo różni się od innych klastrów. Dla każdego punktu oblicza się, jak „dobrze” pasuje do swojego klastra w porównaniu do innych – czyli jak „wyraźnie” jego przynależność się odznacza, jak wyraźna jest jego „sylwetka” na tle innych grup. Im wyższy silhouette score, tym wyraźniej punkty tworzą odrębne, dobrze rozdzielone klastry – ich „sylwetki” są wyraźne.

Jak to działa?

Sztucznie usuwamy część znanych wartości w danych (np. losowo zamieniamy część wartości na NaN).
Dla różnych wartości k dokonujemy imputacji braków.
Dla każdej wartości k obliczamy tzw. silhouette score, który mierzy, jak dobrze rozdzielone są dwie grupy: oryginalne wartości oraz wartości imputowane.
Wybieramy takie k, dla którego silhouette score jest najwyższy lub bliski maksimum.

Wzór na silhouette score dla punktu $i$ :

s(i) = \frac{b(i) - a(i)}{\max\{a(i), b(i)\}}

(1)

gdzie:

$a(i)$ – średnia odległość punktu $i$ do wszystkich innych punktów w tej samej grupie (np. oryginalnych lub imputowanych),
$b(i)$ – najmniejsza średnia odległość punktu $i$ do punktów w innej grupie.

Wartość silhouette mieści się w przedziale od -1 do 1. Im bliżej 1, tym lepsze rozdzielenie grup.

Zalety metody:

Pozwala ocenić, czy imputacja nie zaciera struktury danych.
Pomaga wybrać k, które najlepiej oddziela wartości oryginalne od imputowanych.

Wskazówka praktyczna:
Najlepiej wybrać takie k, dla którego silhouette score jest najwyższy lub przestaje wyraźnie rosnąć (tzw. „łokieć” wykresu). Zobaczmy:

from sklearn.impute import KNNImputer
from sklearn.metrics import silhouette_score
from sklearn.preprocessing import StandardScaler
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')

# Przygotowanie danych bez braków
df = df_titanic[['Age', 'Fare']].dropna().copy()
np.random.seed(42)
mask = np.random.rand(len(df)) < 0.2  # 20% losowych braków
df_missing = df.copy()
df_missing.loc[mask, 'Age'] = np.nan

silhouette_scores = []
neighbors = range(2, 16)
for k in neighbors:
    imputer = KNNImputer(n_neighbors=k)
    imputed = imputer.fit_transform(df_missing)
    # Standaryzacja do obliczenia silhouette
    scaler = StandardScaler()
    imputed_scaled = scaler.fit_transform(imputed)
    # Grupujemy na podstawie imputowanych wartości Age (czyli "klastry" wg wartości imputowanych)
    # Tworzymy etykiety: 0 - oryginalne, 1 - imputowane
    labels = np.where(mask, 1, 0)
    score = silhouette_score(imputed_scaled, labels)
    silhouette_scores.append(score)

plt.plot(neighbors, silhouette_scores, marker='o')
plt.xlabel('Liczba sąsiadów (k)')
plt.ylabel('Silhouette score')
plt.title('Metoda Silhouette dla imputera KNN')
plt.show()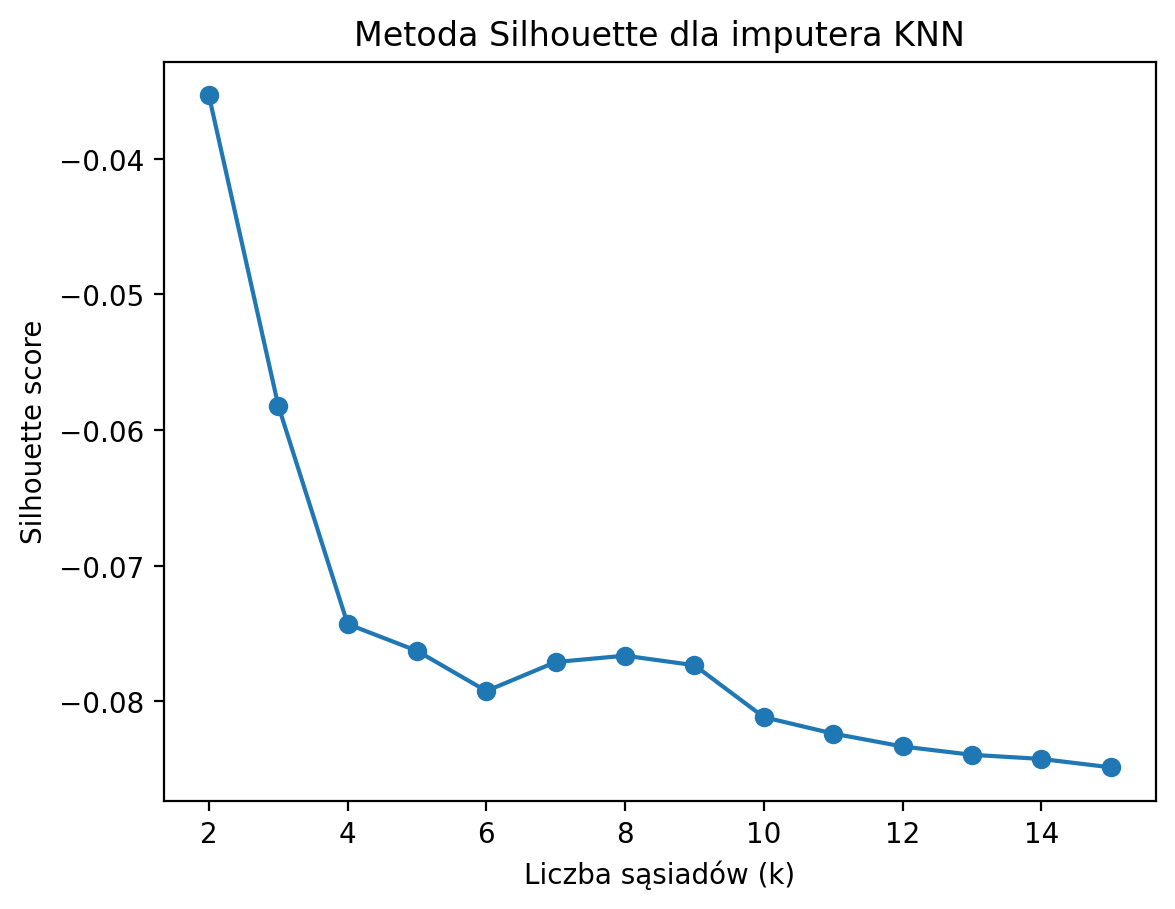

Na wykresie widać, że silhouette score jest najwyższy (najmniej ujemny) dla najmniejszej liczby sąsiadów (k=2), a wraz ze wzrostem k wynik pogarsza się (score spada, staje się bardziej ujemny). Oznacza to, że im większa liczba sąsiadów, tym trudniej odróżnić wartości imputowane od oryginalnych – imputacja staje się coraz bardziej „uśredniona”, a struktura danych się zaciera.

Wniosek:

Najlepszy (najwyższy) silhouette score uzyskujemy dla k=2. W praktyce warto wybrać najmniejsze k, dla którego score jest najwyższy lub przestaje wyraźnie rosnąć. W tym przypadku im mniejsze k, tym lepsze rozdzielenie, więc optymalny wybór to k=2 lub 3.

Dodatkowo, wartości silhouette są ujemne, co oznacza, że rozdzielenie nie jest idealne – ale i tak mniejsze k daje lepszy efekt niż większe.

Ok, a teraz zajmijmy się “prawdziwymi” problemami z brakami danych wybierając 3 sąsiadów w metodzie imputacji braków hotdeck KNN:

Imputacja Hot Deck najbliższego sąsiedztwa (k-NN)¶

from sklearn.impute import KNNImputer

# Tworzymy obiekt KNNImputer
knn_imputer = KNNImputer(n_neighbors=3)  # tutaj wstawiasz optymalną liczbę sąsiadów

# Wybieramy kolumny numeryczne do imputacji
columns_to_impute = ['Age', 'Fare']  # Przykład kolumn
df_titanic[columns_to_impute] = knn_imputer.fit_transform(df_titanic[columns_to_impute])

df_titanic.isna().any()

Podsumowanie¶

Imputacja losowa Hot Deck:

Wartości NaN w kolumnie są zastępowane losową wartością z istniejących danych w tej samej kolumnie.
Jest to szybkie, ale może wprowadzać losowość, która nie uwzględnia zależności między zmiennymi.

Imputacja Hot Deck najbliższego sąsiedztwa (k-NN):

Algorytm k-NN wykorzystuje inne cechy (np. Pclass, Fare), aby znaleźć podobne rekordy i imputować brakujące wartości.
Jest bardziej zaawansowany i uwzględnia relacje między zmiennymi.

Imputacja jednowymiarowa vs. Imputacja wielowymiarowa¶

Imputacja jednowymiarowa: która imputuje wartości w i-tym wymiarze funkcji, wykorzystując tylko wartości, których nie brakuje w tym wymiarze funkcji (np. impute.SimpleImputer).

Algorytmy imputacji wielowymiarowej wykorzystują cały zestaw dostępnych wymiarów cech do oszacowania brakujących wartości (np. impute.IterativeImputer).

import sklearn
from sklearn.impute import SimpleImputer

SimpleImputer¶

Ta klasa zapewnia podstawowe strategie przypisywania brakujących wartości. Brakujące wartości można przypisać za pomocą dostarczonej wartości stałej lub przy użyciu statystyk (średnia, mediana lub najczęstsze) każdej kolumny, w której znajdują się brakujące wartości.

df_sales = pd.read_excel("data/Saless.xlsx")
df_sales.head(5)

Zastąpimy brakujące wartości (NaN) w kolumnie “Day_Temp” średnią wartością tej kolumny:

imputer=SimpleImputer(missing_values=np.nan,strategy='mean')
imputer=imputer.fit(df_sales.iloc[:,3:4]) #oznacza wybór wszystkich wierszy, wybór kolumn o indeksach od 3 do 4 (bez 4), czyli tylko kolumny o indeksie 3.
df_sales.iloc[:,3:4]=imputer.transform(df_sales.iloc[:,3:4])

Zamiast osobno wywoływać fit() i transform(), użyjemy teraz metody fit_transform(), która jednocześnie dopasowuje imputera do danych (oblicza średnią) i przekształca brakujące wartości (NaN) w jednej operacji.

Efekt końcowy jest taki sam: brakujące wartości w czwartej kolumnie (df_saless.iloc[:, 3:4]) zostają zastąpione średnią tej kolumny.

imputer=SimpleImputer(missing_values=np.nan,strategy='mean')

df_sales.iloc[:,3:4]=imputer.fit_transform(df_sales.iloc[:,3:4])

Zastąpić mozemy brakujące wartości (NaN) w dwóch kolumnach (Day_Temp i No_of_Customers, zakładając, że są to kolumny o indeksach 3 i 4) średnimi wartościami odpowiednich kolumn.

imputer=SimpleImputer(missing_values=np.nan,strategy='mean')
imputer=imputer.fit(df_sales.iloc[:,3:5])
df_sales.iloc[:,3:5]=imputer.transform(df_sales.iloc[:,3:5])

Klasa SimpleImputer obsługuje również dane kategoryczne reprezentowane jako wartości łańcuchowe lub kategorie pandas przy użyciu strategii „most_frequent” lub „constant”:

df = pd.DataFrame([["a", "x"],
                    [np.nan, "y"],
                    ["a", np.nan],
                    ["b", "y"]], dtype="category")
df

imp = SimpleImputer(strategy="most_frequent")
print(imp.fit_transform(df))

[['a' 'x']
 ['a' 'y']
 ['a' 'y']
 ['b' 'y']]

imp_cat = SimpleImputer(missing_values=np.nan, strategy="most_frequent")

Zastępujemy teraz brakujące wartości (NaN) w ostatniej kolumnie df_sales najczęściej występującą wartością w tej kolumnie.

imp_cat to obiekt SimpleImputer z ustawioną strategią “most_frequent”, co oznacza, że brakujące wartości zostaną zastąpione najczęściej; df_saless.iloc[:, -1:] wybiera ostatnią kolumnę w DataFrame jako DataFrame (zachowując dwuwymiarową strukturę).

#imp_cat.fit_transform(df_saless.iloc[:,-1:])
df_sales.iloc[:,-1:] = imp_cat.fit_transform(df_sales.iloc[:,-1:])

df_sales

Jeśli chcemy zastąpić określoną wartość wartością NaN, używamy strategii z fill_value:

imp_cat = SimpleImputer(missing_values=np.nan, strategy="constant",fill_value='G')

df_sales.iloc[:,-1:] = imp_cat.fit_transform(df_sales.iloc[:,-1:])

df_sales

IterativeImputer¶

A teraz omówimy kilka przykładów użycia klasy IterativeImputer z biblioteki sklearn.impute, która umożliwia imputację brakujących wartości w danych przy użyciu iteracyjnych modeli regresji.

Możesz użyć innych modeli jako estymatorów w IterativeImputer, takich jak:

LinearRegression (klasyczna regresja liniowa).
DecisionTreeRegressor (drzewa decyzyjne).
RandomForestRegressor (las losowy).
KNeighborsRegressor (regresja k-najbliższych sąsiadów).

IterativeImputer działa w ten sposób, że iteracyjnie przewiduje brakujące wartości w jednej kolumnie na podstawie pozostałych kolumn, używając modelu regresji.

from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import IterativeImputer
from sklearn.linear_model import LinearRegression

data = {
    'A': [1, 2, np.nan, 4],
    'B': [5, np.nan, 7, 8],
    'C': [np.nan, 11, 12, 13]
}
df = pd.DataFrame(data)

# Tworzymy obiekt IterativeImputer z modelem LinearRegression
imputer = IterativeImputer(estimator=LinearRegression(), max_iter=10, random_state=42)

# Dopasowujemy i transformujemy dane
df_imputed = pd.DataFrame(imputer.fit_transform(df), columns=df.columns)

print("Oryginalne dane:")
print(df)
print("\nDane po imputacji:")
print(df_imputed)

Oryginalne dane:
     A    B     C
0  1.0  5.0   NaN
1  2.0  NaN  11.0
2  NaN  7.0  12.0
3  4.0  8.0  13.0

Dane po imputacji:
          A         B     C
0  1.000000  5.000000  12.0
1  2.000000  6.666667  11.0
2  2.714286  7.000000  12.0
3  4.000000  8.000000  13.0

Różnica między IterativeImputer(max_iter=10, random_state=0) a IterativeImputer(estimator=LinearRegression(), max_iter=10, random_state=0) polega na domyślnym estymatorze używanym do imputacji brakujących wartości: IterativeImputer(max_iter=10, random_state=0) domyślnie używa modelu BayesianRidge jako estymatora do przewidywania brakujących wartości:

from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import IterativeImputer

data = {
    'A': [1, 2, np.nan, 4],
    'B': [5, np.nan, 7, 8],
    'C': [np.nan, 11, 12, 13]
}
df = pd.DataFrame(data)

# Tworzymy obiekt IterativeImputer
imputer = IterativeImputer(max_iter=10, random_state=0)

# Dopasowujemy i transformujemy dane
df_imputed = pd.DataFrame(imputer.fit_transform(df), columns=df.columns)

print("Oryginalne dane:")
print(df)
print("\nDane po imputacji:")
print(df_imputed)

Oryginalne dane:
     A    B     C
0  1.0  5.0   NaN
1  2.0  NaN  11.0
2  NaN  7.0  12.0
3  4.0  8.0  13.0

Dane po imputacji:
          A         B          C
0  1.000000  5.000000  11.999923
1  2.000000  6.666646  11.000000
2  2.714292  7.000000  12.000000
3  4.000000  8.000000  13.000000

Ponizszy kod tworzy obiekt IterativeImputer z wykorzystaniem modelu regresji BayesianRidge jako estymatora do imputacji brakujących wartości w danych.

W przeciwieństwie do klasycznej regresji liniowej, BayesianRidge traktuje współczynniki regresji jako zmienne losowe z rozkładem prawdopodobieństwa. Model zakłada priorytetowy rozkład normalny dla współczynników i aktualizuje go na podstawie danych, aby uzyskać rozkład posteriori.

from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import IterativeImputer
from sklearn.linear_model import BayesianRidge

data = {
    'X1': [1, 2, np.nan, 4],
    'X2': [np.nan, 3, 6, 8],
    'X3': [7, 8, 9, np.nan]
}
df = pd.DataFrame(data)

# Tworzymy obiekt IterativeImputer z modelem BayesianRidge
imputer = IterativeImputer(estimator=BayesianRidge(), max_iter=10, random_state=42)

df_imputed = pd.DataFrame(imputer.fit_transform(df), columns=df.columns)

print("Oryginalne dane:")
print(df)
print("\nDane po imputacji:")
print(df_imputed)

Oryginalne dane:
    X1   X2   X3
0  1.0  NaN  7.0
1  2.0  3.0  8.0
2  NaN  6.0  9.0
3  4.0  8.0  NaN

Dane po imputacji:
         X1        X2        X3
0  1.000000  0.746042  7.000000
1  2.000000  3.000000  8.000000
2  3.162385  6.000000  9.000000
3  4.000000  8.000000  9.792037

Imputacja wielokrotna¶

Zamiast jednej imputacji, można wykonać wiele imputacji i połączyć wyniki, aby uwzględnić niepewność w brakujących danych.

Biblioteka statsmodels oferuje funkcję MICE (Multiple Imputation by Chained Equations).

from statsmodels.imputation.mice import MICEData

# Tworzymy przykładowy DataFrame z brakującymi wartościami
data = {
    'Wzrost': [170, 165, np.nan, 180, 175],
    'Waga': [65, np.nan, 70, 80, 75],
    'Wiek': [25, 30, 35, np.nan, 40]
}
df = pd.DataFrame(data)

# Tworzymy obiekt MICEData
mice_data = MICEData(df)

# Iteracyjna imputacja brakujących wartości
for i in range(5):  # Wykonujemy 5 iteracji imputacji
    mice_data.update_all()

# Uzyskanie imputowanego DataFrame
df_imputed = mice_data.data

print("Oryginalne dane:")
print(df)
print("\nDane po imputacji:")
print(df_imputed)

Oryginalne dane:
   Wzrost  Waga  Wiek
0   170.0  65.0  25.0
1   165.0   NaN  30.0
2     NaN  70.0  35.0
3   180.0  80.0   NaN
4   175.0  75.0  40.0

Dane po imputacji:
   Wzrost  Waga  Wiek
0   170.0  65.0  25.0
1   165.0  80.0  30.0
2   180.0  70.0  35.0
3   180.0  80.0  40.0
4   175.0  75.0  40.0

Wyjaśnienie:

Dane wejściowe: Przykładowy DataFrame zawiera brakujące wartości w kolumnach Wzrost, Waga i Wiek.
Obiekt MICEData: Tworzymy obiekt, który przechowuje dane i wykonuje imputację wielokrotną.
Iteracje: W pętli wykonujemy 5 iteracji imputacji, aby poprawić jakość oszacowań brakujących wartości.
Wynik: Po zakończeniu imputacji uzyskujemy DataFrame z uzupełnionymi brakującymi wartościami.

Ten przykład pokazuje, jak można iteracyjnie imputować brakujące dane w różnych kolumnach.

Różnica między single imputation (imputacją pojedynczą) a multiple imputation (imputacją wielokrotną) polega na sposobie radzenia sobie z niepewnością dotyczącą brakujących danych

W single imputation wartości brakujące są zastępowane jedną oszacowaną wartością (np. średnią, medianą, modą, wartością przewidywaną przez model itp.).

W multiple imputation brakujące wartości są imputowane wielokrotnie, tworząc kilka różnych zestawów danych, w których brakujące wartości są zastąpione różnymi oszacowaniami. Następnie wyniki analizy są łączone, aby uwzględnić niepewność imputacji. Jest to podejście bardziej precyzyjne i mniej stronnicze wyniki w porównaniu do imputacji pojedynczej. Zachowuje wariancję w danych.

Cecha	Single Imputation	Multiple Imputation
Liczba imputacji	Jedna wartość na brakujący punkt	Wiele wartości na brakujący punkt
Uwzględnienie niepewności	Nie	Tak
Złożoność	Prosta	Złożona
Wariancja danych	Może być zaniżona	Zachowana
Przykład	Średnia, mediana	MICE (Multiple Imputation by Chained Equations)

Jak działa Multiple Imputation?

Proces składa się z trzech głównych kroków:

Imputacja brakujących danych w wielu iteracjach:

Brakujące wartości są imputowane wielokrotnie, tworząc kilka różnych zestawów danych (np. 5-10 zestawów).
Każda imputacja jest wykonywana na podstawie rozkładu prawdopodobieństwa, co pozwala uwzględnić niepewność związaną z brakującymi danymi.

Analiza każdego zestawu danych:

Każdy zestaw danych jest analizowany osobno, tak jakby był kompletny.
Wyniki analizy (np. średnie, odchylenia standardowe, współczynniki regresji) są zapisywane dla każdego zestawu.

Łączenie wyników:

Wyniki z poszczególnych zestawów danych są łączone w jeden ostateczny wynik.
Uwzględnia się zarówno wariancję między imputowanymi zestawami danych, jak i wariancję wewnątrz każdego zestawu.

Przykład zastosowania Multiple Imputation

Załóżmy, że mamy zbiór danych z brakującymi wartościami w kolumnie Age. Proces Multiple Imputation mógłby wyglądać następująco:

Imputacja:

W pierwszej iteracji brakujące wartości Age są imputowane na podstawie średniej i wariancji.
W drugiej iteracji wartości są imputowane na podstawie innego losowego rozkładu.
Proces powtarza się np. 5 razy, tworząc 5 różnych zestawów danych.

Analiza:

Na każdym z 5 zestawów danych przeprowadzana jest analiza, np. regresja liniowa.

Łączenie wyników:

Wyniki z 5 analiz są łączone, uwzględniając różnice między zestawami danych.

Popularne algorytmy Multiple Imputation

MICE (Multiple Imputation by Chained Equations):

Najczęściej stosowana metoda.
Imputuje brakujące wartości iteracyjnie, przewidując je na podstawie innych zmiennych w zbiorze danych.

PMM (Predictive Mean Matching):

Imputuje brakujące wartości na podstawie podobnych obserwacji w danych.

Bayesian Imputation:

Wykorzystuje modele bayesowskie do imputacji brakujących danych.

Uwaga: MICEData z biblioteki statsmodels nie pozwala na wybór konkretnego algorytmu do imputacji. Domyślnie używa prostych modeli regresji liniowej do przewidywania brakujących wartości na podstawie innych zmiennych w zbiorze danych. Jeśli chcesz użyć bardziej zaawansowanych algorytmów (np. lasów losowych, k-NN), musisz skorzystać z innych narzędzi, takich jak IterativeImputer z sklearn, który umożliwia wybór estymatora (np. RandomForestRegressor, KNeighborsRegressor

Zadanie domowe - do dyskusji¶

Zadanko domowe: zastosuj do wybranego przez ciebie zbioru danych metodę imputacji MICE oraz np. Random Forest lub knn.

Porównaj otrzymane predykcje braków.

## Twój kod tutaj

Brudne dane¶

Wiele razy spędzamy godziny na rozwiązywaniu problemów z brakującymi wartościami, niespójnościami logicznymi lub wartościami odstającymi w naszych zbiorach danych. W tym poradniku omówimy najpopularniejsze techniki oczyszczania danych.

Będziemy pracować z nieuporządkowanym zbiorem danych iris. Pierwotnie opublikowany w UCI Machine Learning Repository: Iris Data Set, ten niewielki zbiór danych z 1936 roku jest często używany do testowania algorytmów uczenia maszynowego i wizualizacji. Każdy wiersz tabeli reprezentuje kwiat irysa, w tym jego gatunek i wymiary jego części botanicznych, działki i płatka, w centymetrach.

Zapoznaj się z tym zestawem danych tutaj:

dirty_iris = pd.read_csv("data/dirty_iris.csv")
dirty_iris.head(3)

Spójne dane to technicznie poprawne dane, które nadają się do analizy statystycznej. Są to dane, w których brakujące wartości, wartości specjalne, (oczywiste) błędy i wartości odstające zostały usunięte, skorygowane lub przypisane. Dane są zgodne z ograniczeniami opartymi na rzeczywistej wiedzy na temat przedmiotu, który dane opisują.

Mamy następującą wiedzę podstawową:

Gatunek powinien być jedną z następujących wartości: setosa, versicolor lub virginica.
Wszystkie zmierzone właściwości liczbowe wymiarów powinny być dodatnie.
Długość płatka irysa jest co najmniej 2 razy większa od jego szerokości.
Długość działki irysa nie może przekraczać 30 cm.
Działki irysa są dłuższe niż jego płatki.

Zdefiniujemy teraz te reguły w osobnym obiekcie „RULES” i wczytamy je do Pythona. Wydrukujemy wynikowy obiekt ograniczenia:

# Definiujemy reguły jako funkcje:
def check_rules(df):
    rules = {
        "Sepal.Length <= 30": df["Sepal.Length"] <= 30,
        "Species in ['setosa', 'versicolor', 'virginica']": df["Species"].isin(['setosa', 'versicolor', 'virginica']),
        "Sepal.Length > 0": df["Sepal.Length"] > 0,
        "Sepal.Width > 0": df["Sepal.Width"] > 0,
        "Petal.Length > 0": df["Petal.Length"] > 0,
        "Petal.Width > 0": df["Petal.Width"] > 0,
        "Petal.Length >= 2 * Petal.Width": df["Petal.Length"] >= 2 * df["Petal.Width"],
        "Sepal.Length > Petal.Length": df["Sepal.Length"] > df["Petal.Length"]
    }
    return rules

# Reguły do ramki danych:
rules = check_rules(dirty_iris)

# Wydruk:
for rule, result in rules.items():
    print(f"{rule}: {result.all()}")

Sepal.Length <= 30: False
Species in ['setosa', 'versicolor', 'virginica']: True
Sepal.Length > 0: False
Sepal.Width > 0: False
Petal.Length > 0: False
Petal.Width > 0: False
Petal.Length >= 2 * Petal.Width: False
Sepal.Length > Petal.Length: False

Teraz możemy określić, jak często każda reguła jest łamana (naruszenia). Możemy również podsumować i wykreślić wynik.

# Sprawdzamy naruszenia reguł:
violations = {rule: ~result for rule, result in rules.items()}

# Podsumowujemy je:
summary = {rule: result.sum() for rule, result in violations.items()}

# Wydruczek:
print("Summary of Violations:")
for rule, count in summary.items():
    print(f"{rule}: {count} violations")

Summary of Violations:
Sepal.Length <= 30: 12 violations
Species in ['setosa', 'versicolor', 'virginica']: 0 violations
Sepal.Length > 0: 11 violations
Sepal.Width > 0: 19 violations
Petal.Length > 0: 20 violations
Petal.Width > 0: 12 violations
Petal.Length >= 2 * Petal.Width: 34 violations
Sepal.Length > Petal.Length: 30 violations

Jaki procent % danych ma błędy?

import matplotlib.pyplot as plt
# Wykres naruszeń:
violation_counts = pd.Series(summary)
ax = violation_counts.plot(kind='bar', figsize=(10, 6))
plt.title('Podsumowanie błędów w danych')
plt.xlabel('Reguły')
plt.ylabel('Liczba błędów')

# Dodaję procenty nad słupki:
for p in ax.patches:
    ax.annotate(f'{p.get_height() / len(dirty_iris) * 100:.1f}%', 
                (p.get_x() + p.get_width() / 2., p.get_height()), 
                ha='center', va='center', xytext=(0, 10), 
                textcoords='offset points')

plt.show()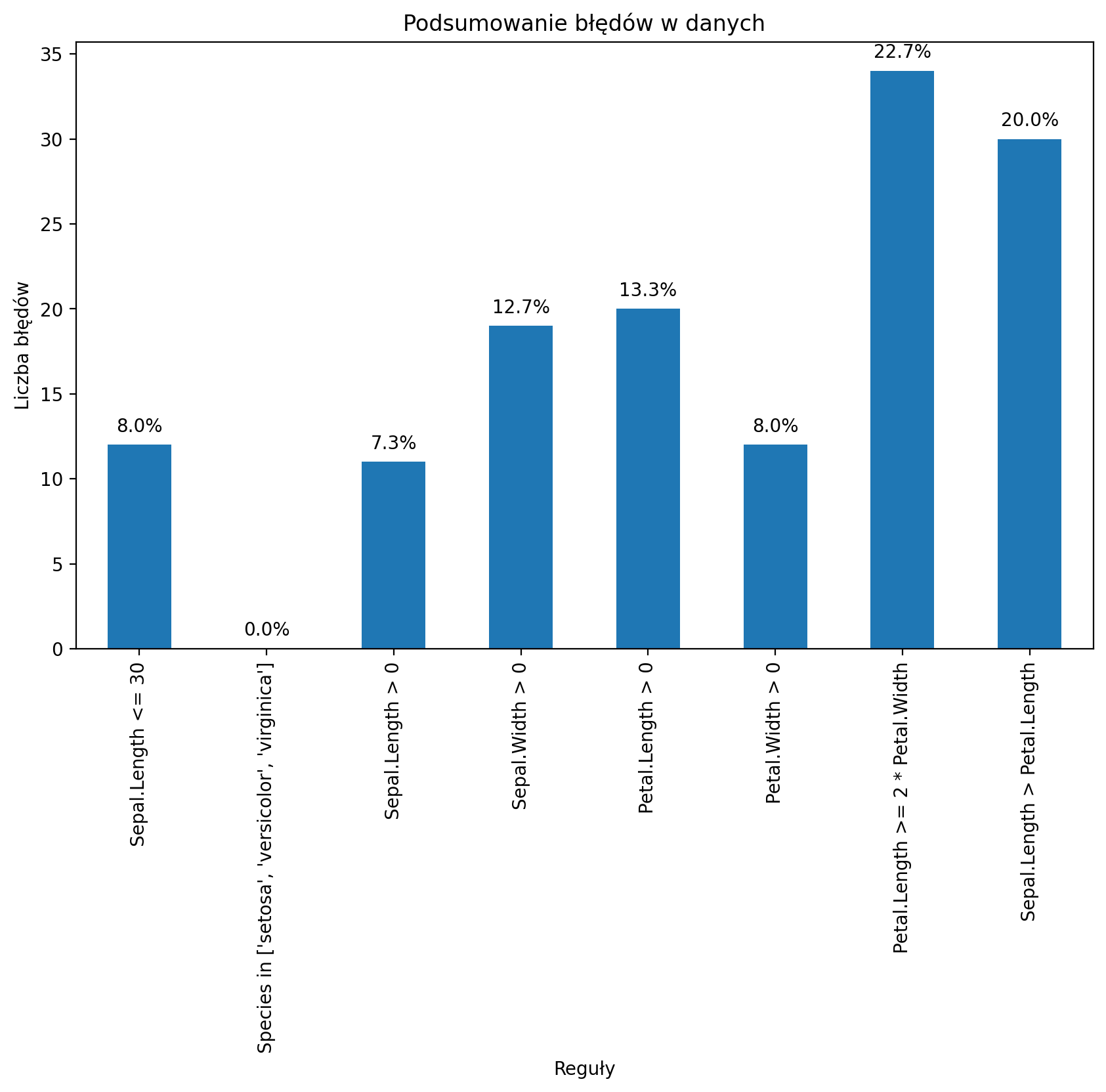

Sprawdź, które kwiaty mają zbyt długie działki kielicha, korzystając z wyników naruszeń.

violations = {rule: ~result for rule, result in rules.items()}
violated_df = pd.DataFrame(violations)
violated_rows = dirty_iris[violated_df["Sepal.Length <= 30"]]
print(violated_rows)

     Sepal.Length  Sepal.Width  Petal.Length  Petal.Width     Species
14            NaN          3.9          1.70          0.4      setosa
18            NaN          4.0           NaN          0.2      setosa
24            NaN          3.0          5.90          2.1   virginica
27           73.0         29.0         63.00          NaN   virginica
29            NaN          2.8          0.82          1.3  versicolor
57            NaN          2.9          4.50          1.5  versicolor
67            NaN          3.2          5.70          2.3   virginica
113           NaN          3.3          5.70          2.1   virginica
118           NaN          3.0          5.50          2.1   virginica
119           NaN          2.8          4.70          1.2  versicolor
124          49.0         30.0         14.00          2.0      setosa
137           NaN          3.0          4.90          1.8   virginica

Znajdźmy wartości odstające w długości działki przy użyciu metody boxplot.

Pobierzemy odpowiednie obserwacje i sprawdź pozostałe wartości.

Jakieś pomysły, co mogło się stać?

Ustawimy wartości odstające na NA (lub wartość, którą uznasz za bardziej odpowiednią).

plt.figure(figsize=(10, 6))
plt.boxplot(dirty_iris['Sepal.Length'].dropna())
plt.title('Wykres pudełkowy Sepal Length')
plt.ylabel('Sepal Length')
plt.show()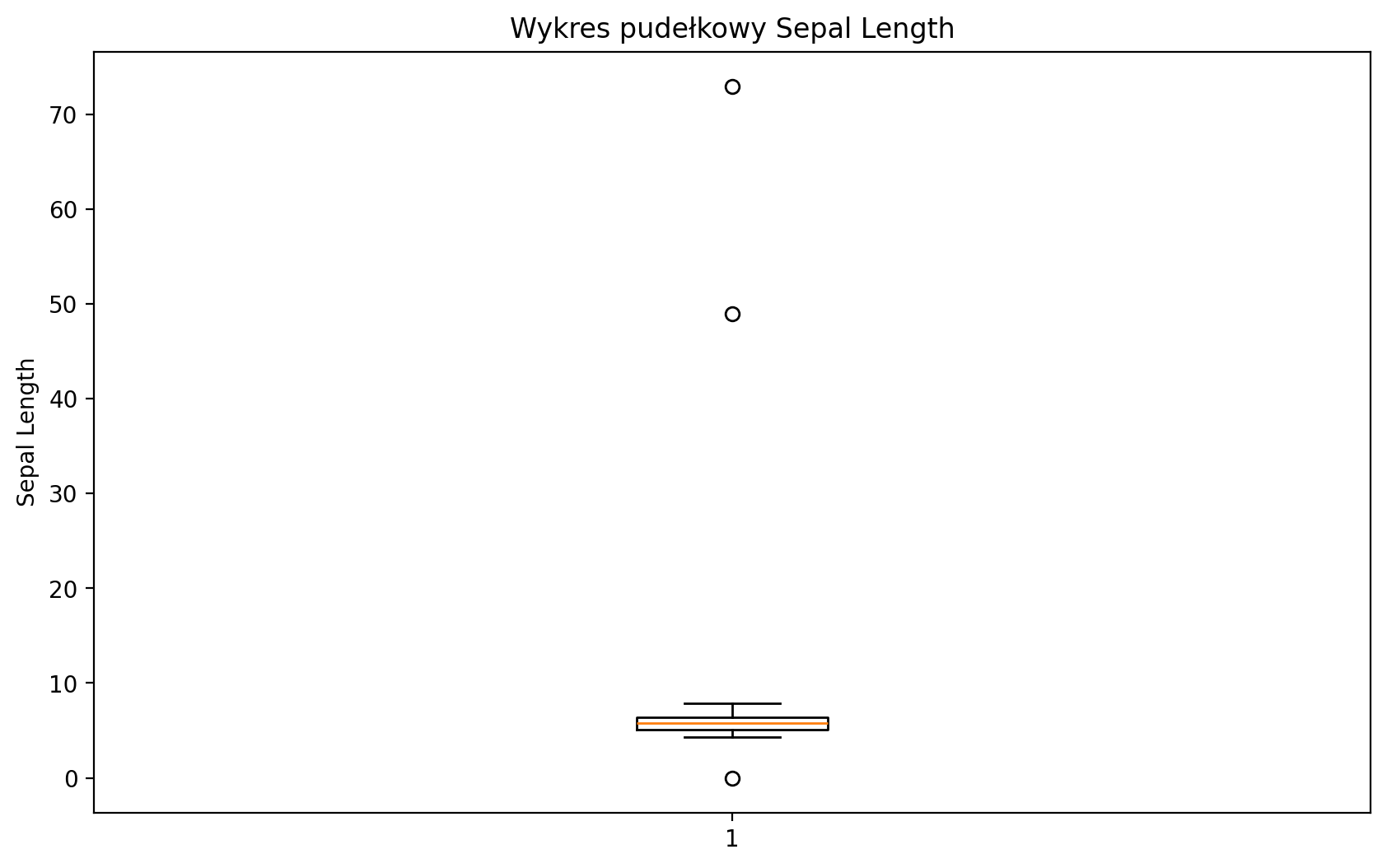

# Znajdziemy obserwacje odstające:
outliers = dirty_iris['Sepal.Length'][np.abs(dirty_iris['Sepal.Length'] - dirty_iris['Sepal.Length'].mean()) > (1.5 * dirty_iris['Sepal.Length'].std())]
outliers_idx = dirty_iris.index[dirty_iris['Sepal.Length'].isin(outliers)]

# Wydrukujemy je:
print("Odstające:")
print(dirty_iris.loc[outliers_idx])

Odstające:
     Sepal.Length  Sepal.Width  Petal.Length  Petal.Width    Species
27           73.0         29.0          63.0          NaN  virginica
124          49.0         30.0          14.0          2.0     setosa

Wszystkie wydają się za duże... może były mierzone w mm zamiast w cm?

# Skorygujemy wartości odstające (zakładając, że zostały zmierzone w mm zamiast w cm).
dirty_iris.loc[outliers_idx, ['Sepal.Length', 'Sepal.Width', 'Petal.Length', 'Petal.Width']] /= 10

plt.figure(figsize=(10, 6))
sns.boxplot(x='Species', y='Sepal.Length', data=dirty_iris)
plt.title('Wykres pudełkowy Sepal Length wg Gatunku')
plt.xlabel('Gatunek')
plt.ylabel('Sepal Length')
plt.show()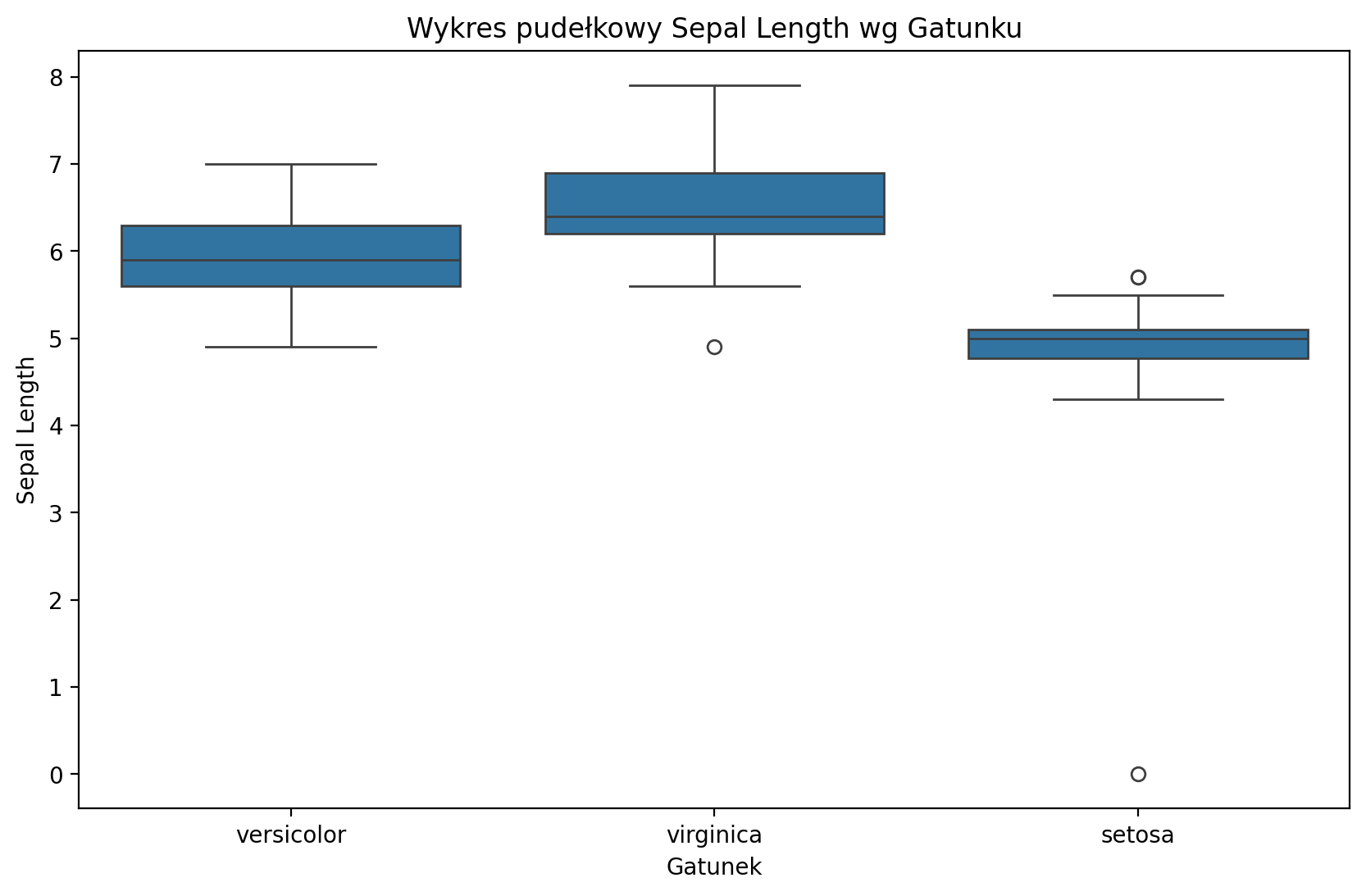

Zwróćmy uwagę, że prosty boxplot pokazuje dodatkową wartość odstającą!

Korekta błędów¶

Zastąpmy wartości niedodatnie z Sepal.Width wartością NA:

# Definiujemy regułę korekty:
def correct_sepal_width(df):
    df.loc[(~df['Sepal.Width'].isna()) & (df['Sepal.Width'] <= 0), 'Sepal.Width'] = np.nan
    return df

# Stosujemy korektę dla ramki danych:
mydata_corrected = correct_sepal_width(dirty_iris)

# i obejrzyjmy dane:
print(mydata_corrected)

     Sepal.Length  Sepal.Width  Petal.Length  Petal.Width     Species
0             6.4          3.2           4.5          1.5  versicolor
1             6.3          3.3           6.0          2.5   virginica
2             6.2          NaN           5.4          2.3   virginica
3             5.0          3.4           1.6          0.4      setosa
4             5.7          2.6           3.5          1.0  versicolor
..            ...          ...           ...          ...         ...
145           6.7          3.1           5.6          2.4   virginica
146           5.6          3.0           4.5          1.5  versicolor
147           5.2          3.5           1.5          0.2      setosa
148           6.4          3.1           NaN          1.8   virginica
149           5.8          2.6           4.0          NaN  versicolor

[150 rows x 5 columns]

Zastąpienie wszystkich błędnych wartości wartością NA przy użyciu (wyniku) localizeErrors:

# stosujemy reguły dla naruszeń (błędów):
rules = check_rules(dirty_iris)
violations = {rule: ~result for rule, result in rules.items()}
violated_df = pd.DataFrame(violations)

# lokalizujemy błędy i zamieniamy je na NA:
for col in violated_df.columns:
    dirty_iris.loc[violated_df[col], col.split()[0]] = np.nan

Twoja kolej!¶

Lepiej mieć NA, niz błędy w danych. Moznaby było ewentualnie pokusić się teraz o imputację nowopowstałych braków...

## Twój kod tutaj

Duplikaty¶

Duplikaty w danych to wiersze, które są identyczne w każdej kolumnie lub w wybranym podzbiorze kolumn. Mogą one prowadzić do błędnych analiz, ponieważ nadmiernie wpływają na wyniki statystyczne i modele.

Zduplikowane obserwacje najczęściej pojawiają się podczas gromadzenia danych, na przykład gdy:

Łączymy zbiory danych z wielu miejsc
Scraping danych (zbieranie danych poprzez scraping stron internetowych)
Otrzymujemy dane od klientów/innych działów jeśli używamy scraping, może się zdarzyć, że zeskrobujemy tę samą stronę internetową więcej niż raz lub te same informacje z dwóch różnych stron.

Bez względu na przyczynę, duplikacja może prowadzić do błędnych wniosków, prowadząc nas do przekonania, że niektóre obserwacje są bardziej powszechne niż w rzeczywistości.

Jak zidentyfikować duplikaty?¶

W Pythonie możemy użyć metody .duplicated() z biblioteki pandas, aby sprawdzić, które wiersze są duplikatami.

# Sprawdzenie, które wiersze są duplikatami
df.duplicated()

Metoda .duplicated() zwraca True dla wszystkich wierszy, które są duplikatami wcześniejszych wierszy.

Jak policzyć liczbę duplikatów?

Aby policzyć liczbę duplikatów w zbiorze danych, możemy użyć:

# tworzymy dane z duplikatami
df = pd.DataFrame({"Name":["John", "Rock", "Neil", "Tom","John","John"], "Rank":[1,2,3,6,1,1], "Marks":[98,59,97,99,98,98]})
df

# Liczba duplikatów
df.duplicated().sum()

np.int64(2)

# pokaz duplikaty
df.loc[df.duplicated(keep=False)]

# Odrzuca duplikaty z wyjątkiem pierwszego wystąpienia.
df1 = df.drop_duplicates(keep='first')
df1

# usuwa wszystkie zduplikowane wiersze
df2 = df.drop_duplicates(keep=False) 
df2

# Usuwa duplikaty z wyjątkiem ostatniego wystąpienia.
df3 = df.drop_duplicates(keep="last")
df3

# zmiana zestawu danych poprzez ustawienie inplace na true
df.drop_duplicates(keep='first', inplace=True)
df

Duplikaty - przykład¶

df_adult = pd.read_csv("data/wrangling/adult.csv")
df_adult.head(5)

Twoja kolej!¶

Otrzymujesz zbiór danych “adult” i musisz sprawdzić, czy są w nim duplikaty. Jeśli są - rozwiąz problem z nimi związany.

# Twój kod tutaj

Łączenie zbiorów danych¶

Łączenie odnosi się do łączenia różnych zbiorów danych w celu wykorzystania mocy dodatkowych informacji.

Może łączyć zbiory danych jako funkcję:
- Wspólnego okna czasowego.
- Wspólnej tożsamości.

Dlaczego scalać?¶

Każdy zbiór danych zawiera ograniczone informacje.
- Na przykład „PKB” według „roku”.
Ale łączenie zbiorów danych pozwala nam zobaczyć, jak więcej zmiennych jest ze sobą powiązanych i wzajemnie na siebie oddziałuje.
Wiele badań obejmuje lokalizowanie zbiorów danych i zastanawianie się, jak je połączyć.

Jak scalać?¶

W Pythonie, pandas.merge pozwala nam połączyć dwie DataFrame na wspólnej kolumnie (kolumnach).

pd.merge(df1, df2, on = "shared_column")

`merge` w praktyce¶

Dla demonstracji, połączymy dwa zbiory danych lingwistycznych:

Jeden zbiór danych zawiera informacje o Age of Acquisition różnych angielskich słów (Kuperman et al., 2014).
Drugi zbiór danych zawiera informacje o częstotliwości i konkretności angielskich słów (Brysbaert et al., 2014).

Ładujemy dane¶

df_aoa = pd.read_csv("data/wrangling/AoA.csv")
df_aoa.head(1)

df_conc = pd.read_csv("data/wrangling/concreteness.csv")
df_conc.head(1)

Różne rodzaje łączenia¶

Jak widzimy, zbiory danych nie są tej samej wielkości. To pozostawia nam decyzję do podjęcia podczas łączenia.

inner join: Czy zachowujemy tylko słowa w obu zbiorach danych?
left join: Czy zachowujemy wszystkie słowa w jednym zbiorze danych („lewym”), niezależnie od tego, czy występują w drugim?
right join: Czy zachowujemy wszystkie słowa w jednym zbiorze danych („prawym”), niezależnie od tego, czy występują w drugim?
outer join: Czy zachowujemy wszystkie słowa w obu zbiorach, pozostawiając puste (nan) wartości tam, gdzie słowo występuje tylko w jednym zbiorze danych?

df_aoa.shape

(31124, 2)

df_conc.shape

(28612, 4)

`inner` join¶

Dla naszych celów najbardziej sensowne jest użycie inner join.
Pozostawia nam to mniej słów niż występuje w obu zbiorach danych.

df_merged = pd.merge(df_aoa, df_conc, on = "Word", how = "inner")
df_merged.head(2)

df_merged.shape

(23569, 5)

Twoja kolej!¶

Co się stanie, jeśli użyjesz innego rodzaju złączenia, np. outer lub left? Co można zauważyć w „kształcie” wynikowej ramki danych? Czy niektóre wiersze mają wartości nan?

### Twój kod tutaj

Dlaczego `merge` jest tak przydatne¶

Teraz, gdy połączyliśmy nasze zbiory danych, możemy przyjrzeć się, jak zmienne poprzecznie odnoszą się do siebie nawzajem.

sns.scatterplot(data = df_merged, x = 'Concreteness',
                y = 'AoA', alpha = .2 );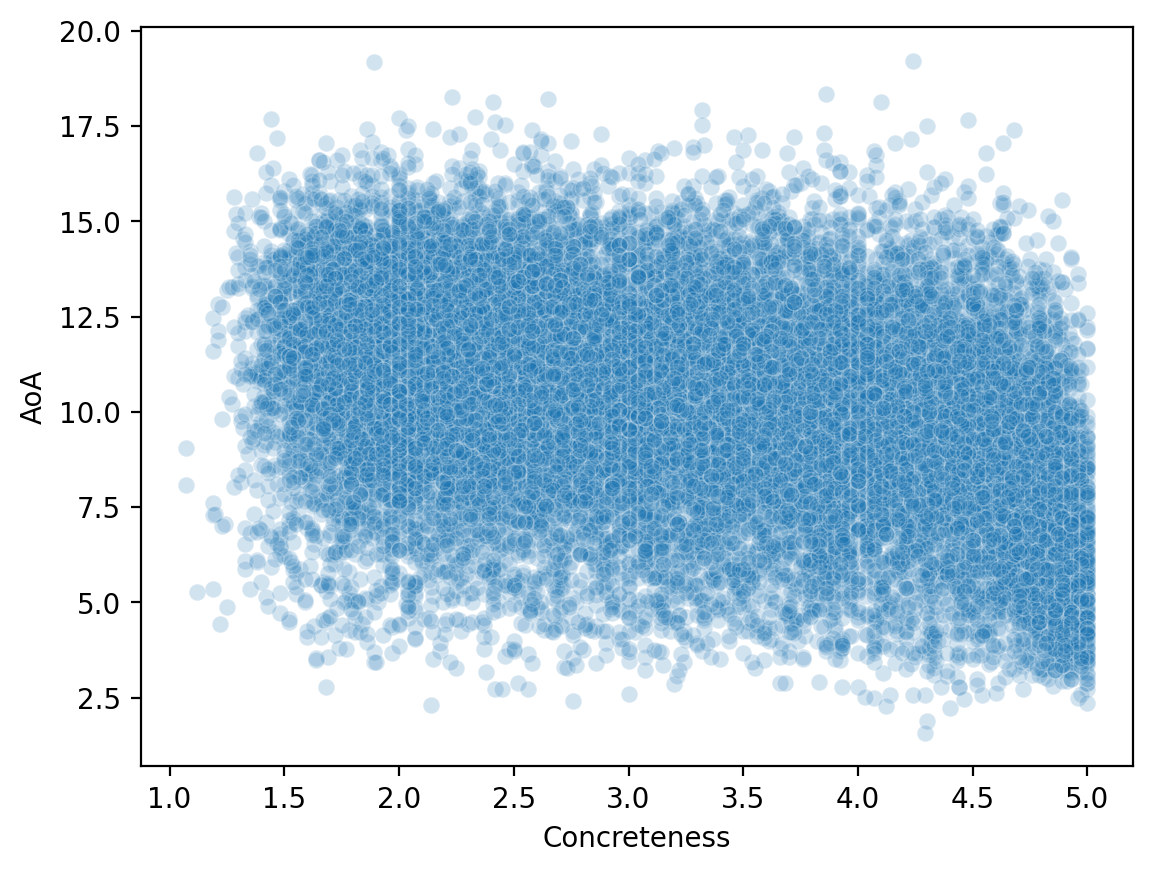

Przekształcanie danych¶

Przekształcanie danych polega na przekształcaniu ich z jednego formatu (np. “szerokiego”) do innego (np. “długiego”), aby uczynić je bardziej podatnymi na wizualizację i analizę.

Często musimy uporządkować nasze dane.

Czym są uporządkowane dane?¶

Porządkowanie danych to szczególny sposób formatowania danych, w którym:

Każda zmienna tworzy kolumnę (np. GDP).
Każda obserwacja tworzy wiersz (np. kraj).
Każdy typ jednostki obserwacji tworzy tabelę (dane tabelaryczne!).

Pierwotnie opracowany przez Hadleya Wickhama, twórcę tidyverse w R.

Uporządkowane vs. “nieuporządkowane” dane¶

Zobaczmy teraz kilka przykładów uporządkowanych vs. nieuporządkowanych danych.

Należy o tym pamiętać:

Wszystkie te zbiory danych zawierają te same informacje, tylko w różnych formatach.
„Nieuporządkowane” dane mogą być przydatne do innych celów, np. do prezentacji w artykule.
Kluczowym celem uporządkowanych danych jest to, że każdy wiersz reprezentuje obserwację.

Uporządkowane dane¶

Pytanie:: Dlaczego te dane są uważane za uporządkowane?

df_tidy = pd.read_csv("data/wrangling/tidy.csv")
df_tidy

Nieuporządkowane dane 1¶

Pytanie:: Dlaczego te dane nie są uważane za uporządkowane?

df_messy1 = pd.read_csv("data/wrangling/messy1.csv")
df_messy1

Nieuporządkowane dane 2¶

Pytanie:: Dlaczego te dane nie są uważane za uporządkowane?

df_messy2 = pd.read_csv("data/wrangling/messy2.csv")
df_messy2

Uporządkowanie danych¶

Na szczęście, pandas umożliwia przekształcenie “nieuporządkowanego” DataFrame w uporządkowany.

Kluczowa funkcja to: pandas.melt.

pd.melt(df, ### dane
        id_vars = [...], ### jakie jest ID kolumny?
        var_name = ..., ### nazwa dla zmiennej grupującej po kolumnach
        value_name = ..., ### nazwa wartości, jaką przyjmuje ta zmienna

Jeśli wydaje się to abstrakcyjne, nie martw się - stanie się jaśniejsze dzięki przykładom!

Zastosujmy `pd.melt`¶

Zacznijmy od naszej pierwszej niechlujnej DataFrame.
Posiada kolumny dla każdego ppt, które zawierają informacje o rt.

df_messy1

pd.melt(df_messy1, id_vars = 'condition', ### condition jest ID zmiennej
       var_name = 'ppt', ### now wiersz dla kazdej obserwacji ppt
       value_name = 'rt') ### etykieta dla zmiennej

Twoja kolej!¶

Spróbuj użyć pd.melt, aby przekształcić df_messy2 w schludną DataFrame.

Wskazówka: Pomyśl o istniejącej strukturze DataFrame - jak dane są pogrupowane - i jakie byłyby id_vars.

df_messy2

### Twój kod tutaj

Prawdziwy zestaw danych¶

Teraz przejdziemy do prawdziwego zestawu danych, który Timothy Lee, twórca Full Stack Economics, skompilował i udostępnił.

df_work = pd.read_csv("data/viz/missing_work.csv")
df_work.head(5)

Twoja kolej!¶

Czy ten zbiór danych jest uporządkowany? Jak moglibyśmy go uporządkować, jeśli nie - tj. gdybyśmy chcieli, aby każdy wiersz był pojedynczą obserwacją odpowiadającą jednemu z powodów braku pracy?

### Twój kod tutaj

Solution¶

df_melted = pd.melt(df_work, id_vars = ['Year', 'Month'],
                    var_name = "Reason",
                    value_name = "Days Missed")
df_melted.head(2)

Dlaczego uporządkowane dane są przydatne¶

Na koniec użyjmy tego zestawu danych do odtworzenia wykresu z FullStackEconomics.

Oryginalny wykres¶

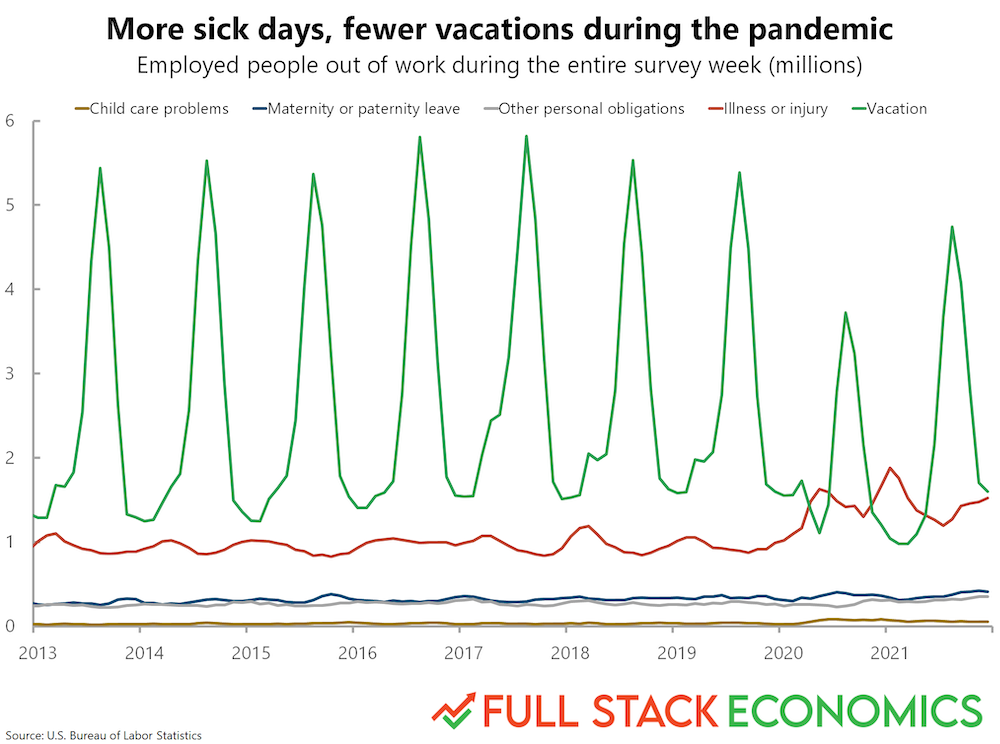
Twoja kolej!¶

Jakich narzędzi z seaborn można użyć do odtworzenia tego wykresu?

### Twój kod tutaj

# %load ./solutions/solution7.py

Transformacje danych¶

Czasami spotykamy się z sytuacją, w której mamy problemy ze skośnymi rozkładami lub po prostu chcemy przekształcić, przekodować lub wykonać dyskretyzację. Przyjrzyjmy się kilku najpopularniejszym metodom transformacji.

Standaryzacja:

Podejście $Z$ -score - procedura standaryzacji, wykorzystująca wzór: $z=\frac{x-\mu}{\sigma}$ , gdzie $\mu$ = średnia, a $\sigma$ = odchylenie standardowe. Wyniki $Z$ są również znane jako wyniki standaryzowane; są to wyniki (lub wartości danych), którym przypisano wspólny standard. Ten standard to średnia równa zero i odchylenie standardowe równe 1.
Podejście minmax - Alternatywnym podejściem do normalizacji (lub standaryzacji) wyniku $Z$ jest tak zwane skalowanie MinMax (często nazywane również po prostu „normalizacją” - co jest częstą przyczyną niejednoznaczności). W tym podejściu dane są skalowane do ustalonego zakresu - zwykle od 0 do 1. Kosztem posiadania tego ograniczonego zakresu - w przeciwieństwie do normalizacji - jest to, że otrzymamy mniejsze odchylenia standardowe, które mogą tłumić efekt wartości odstających. Jeśli chcesz wykonać skalowanie MinMax - po prostu odejmij wartość minimalną i podziel ją przez zakres: $(x-min)/(max-min)$ .

Normalizacja:

Aby rozwiązać problemy z bardzo skośnymi rozkładami, możemy również użyć kilku rodzajów prostych przekształceń:

$log$
$log+1$
$sqrt$
$x^2$
$x^3$

Ćwiczenie: Znormalizuj dochody i przedstaw przekształcony rozkład dochodów na wykresie pudełkowym.

dochody = pd.read_csv("data/models/income.csv")
dochody.head(3)

plt.figure(figsize=(10, 6))
plt.hist(dochody['Income'], edgecolor='black')
plt.title('Histogram dochodów')
plt.xlabel('Dochody')
plt.ylabel('Liczebność')
plt.show()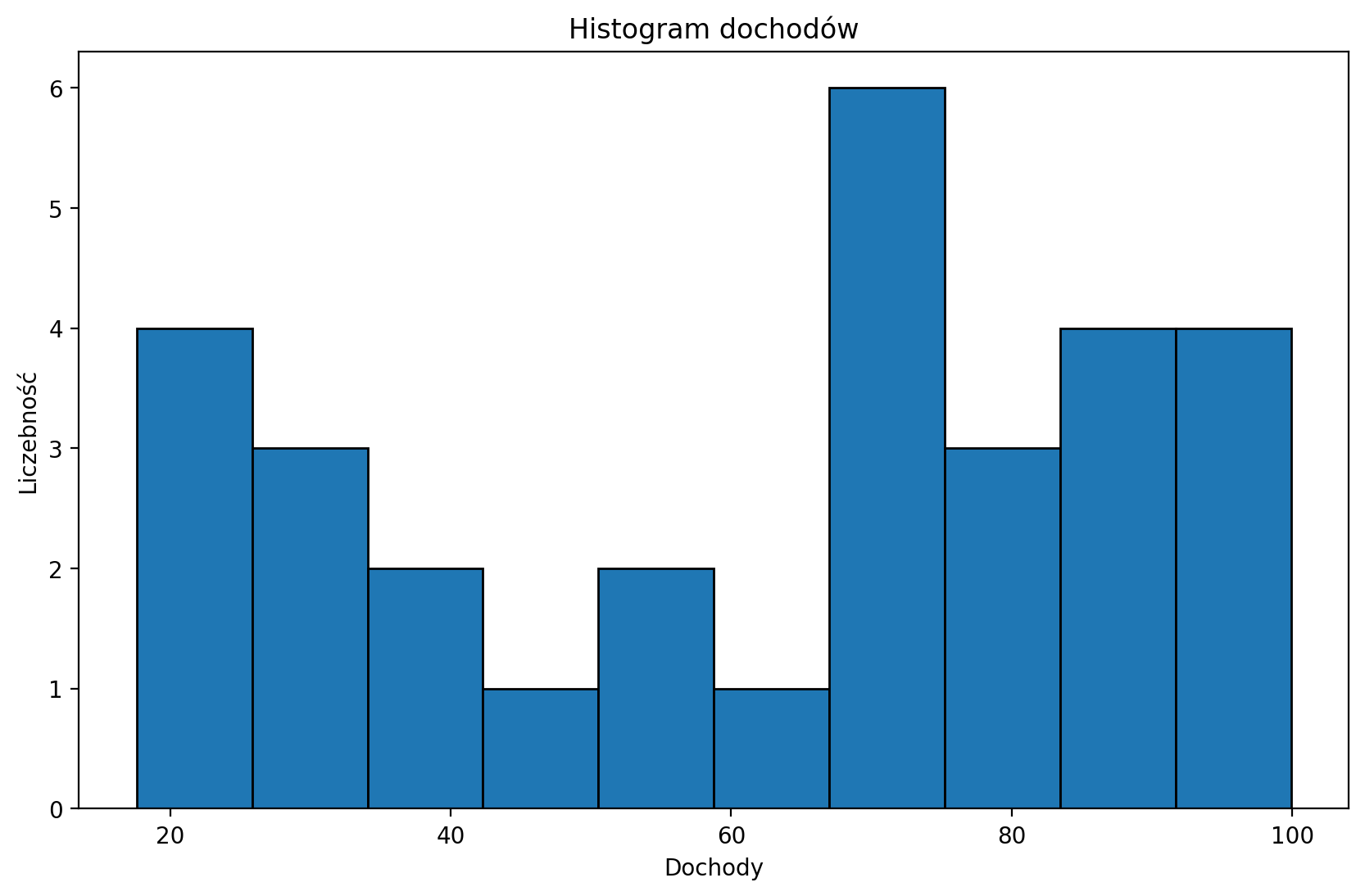

# Twój kod tutaj

Transformacje Boxa - Coxa¶

Transformacja Box-Coxa jest techniką stosowaną podczas przygotowania danych (data wrangling), która pomaga ustabilizować wariancję i przekształcić dane tak, aby były bliższe rozkładowi normalnemu – co jest pożądane w wielu metodach analizy statystycznej i modelowania. Transformacja ta sprawdza się szczególnie dobrze przy danych z prawostronnym skośnym rozkładem. Wymaga dodatnich wartości i polega na znalezieniu optymalnego parametru λ (lambda), który jest dobierany metodą największej wiarygodności.

W Pythonie transformację Box-Coxa można wykonać za pomocą funkcji boxcox z modułu scipy.stats.

Niech $y=(y_1,y_2,…,y_n)$ to dane, do których ma zostać zastosowana transformacja Boxa-Coxa. Box i Cox zdefiniowali swoją transformację jako:

dla $\lambda \neq 0$ :

y{(i)}^{\lambda}=\frac{1}{\lambda}*(y_{i}^{\lambda}-1)

(2)

dla $\lambda = 0$

log(y_i)

(3)

takich jak nieznana $\lambda$ ,

y^\lambda=X* \beta + \epsilon

(4)

gdzie $y^{(\lambda)}$ jest $\lambda$ -transformowanymi danymi, X to macierz projektowa (możliwe kowarianty będące przedmiotem zainteresowania), $\beta$ to zestaw parametrów związanych z danymi przekształconymi w $\lambda$ , a $ϵ = (ϵ_1, ϵ_2, ..., ϵ_n)$ to termin błędu. Ponieważ celem równania (1) jest to, że

y^{(\lambda)} \epsilon ~ N(X* \beta, \sigma^2*I_n), (3)

(5)

wtedy $\epsilon ~ N(0, \sigma^2)$ . Należy zauważyć, że przekształcenie w równaniu (1) jest ważne tylko dla $y_i$ > 0, i = 1, 2, ..., n, a modyfikacje muszą być dokonane, gdy obecne są negatywne obserwacje.

import numpy as np
import pandas as pd
import random
import matplotlib.pyplot as plt
import seaborn as sns

from scipy.stats import boxcox

import warnings
warnings.filterwarnings('ignore')
plt.figure(figsize = (4, 4))
data = np.random.beta(1, 3, 5000) # we create random non normal data (from beta distribution)
sns.distplot(data)
plt.show()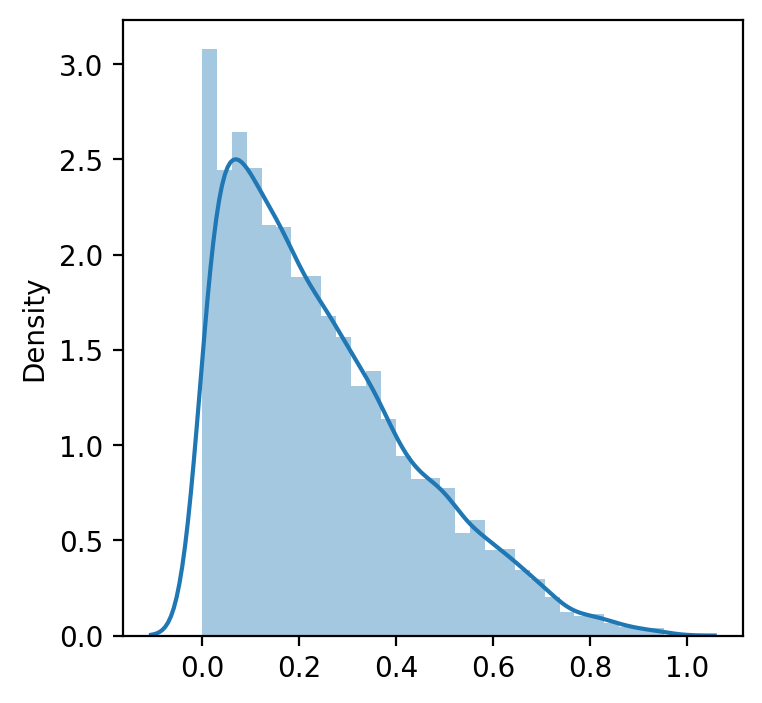

data_transformed, lambda_ = boxcox(data) #Jeśli parametr lambda ma wartość None, drugim zwracanym argumentem jest 
# lambda, która maksymalizuje funkcję log-likelihood.
print('Przekształcone dane do rozkładu normalnego', data_transformed)
print(40*'==')
print('Lambda, która maksymalizuje funkcję logarytmu prawdopodobieństwa dla rozkładu normalnego:', lambda_)

Przekształcone dane do rozkładu normalnego [-2.05593673 -0.93109759 -1.09529997 ... -0.80804333 -0.71891983
 -2.19129002]
================================================================================
Lambda, która maksymalizuje funkcję logarytmu prawdopodobieństwa dla rozkładu normalnego: 0.4084988916110015

manually_transformed = [(i**lambda_ -1)/lambda_ for i in data] # ręcznie

warnings.filterwarnings('ignore')
plt.figure(figsize = (4, 4))
sns.distplot(data_transformed)
plt.show()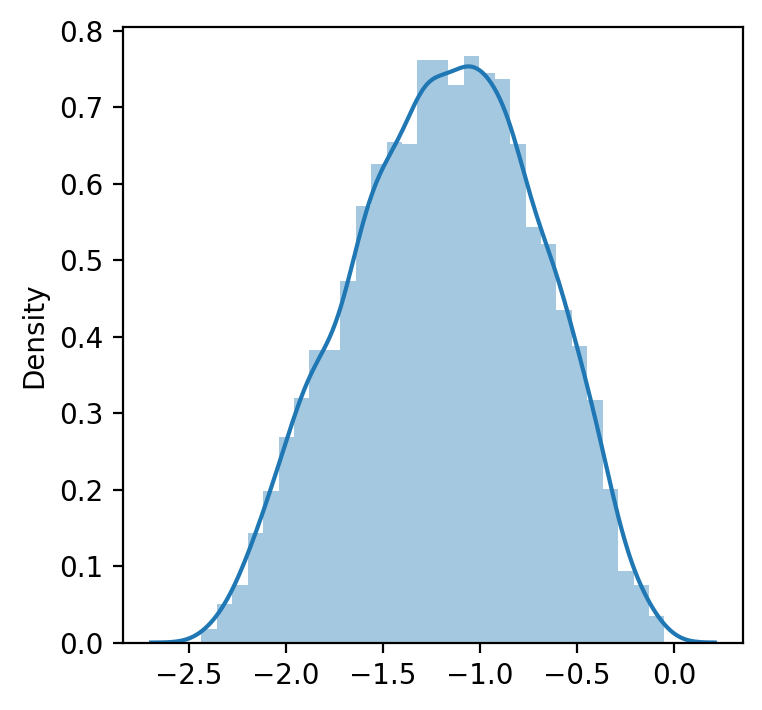

warnings.filterwarnings('ignore')
plt.figure(figsize = (4, 4))
sns.distplot(manually_transformed) # ręcznie dobrana lambda
plt.show()

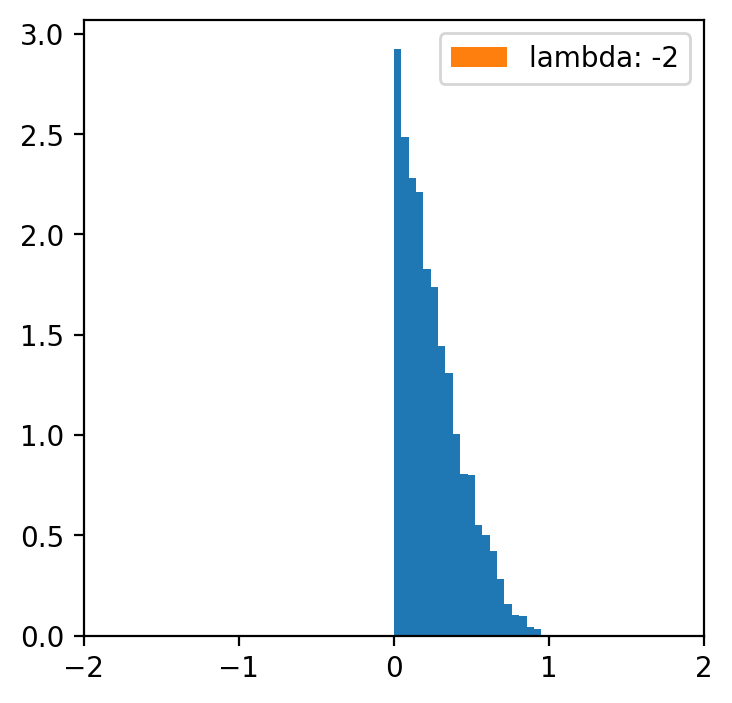
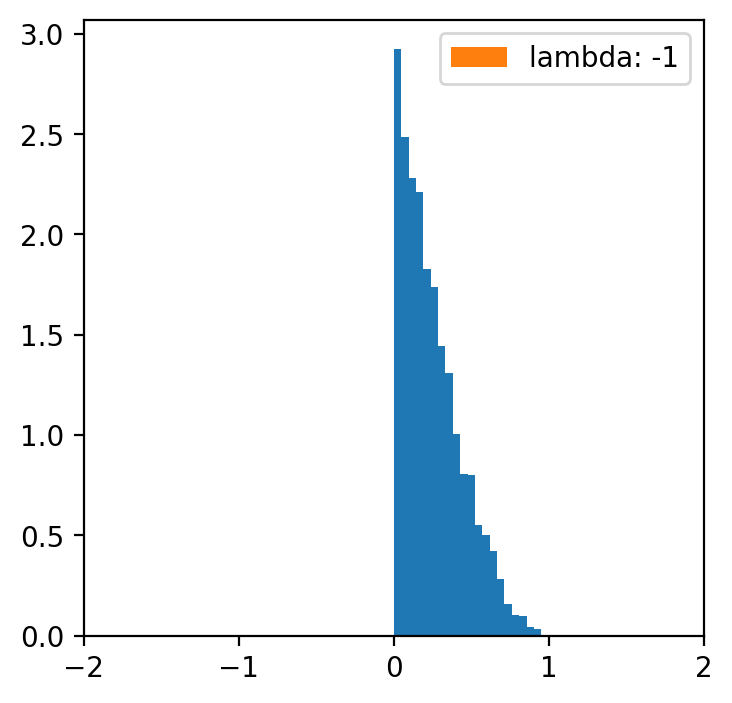
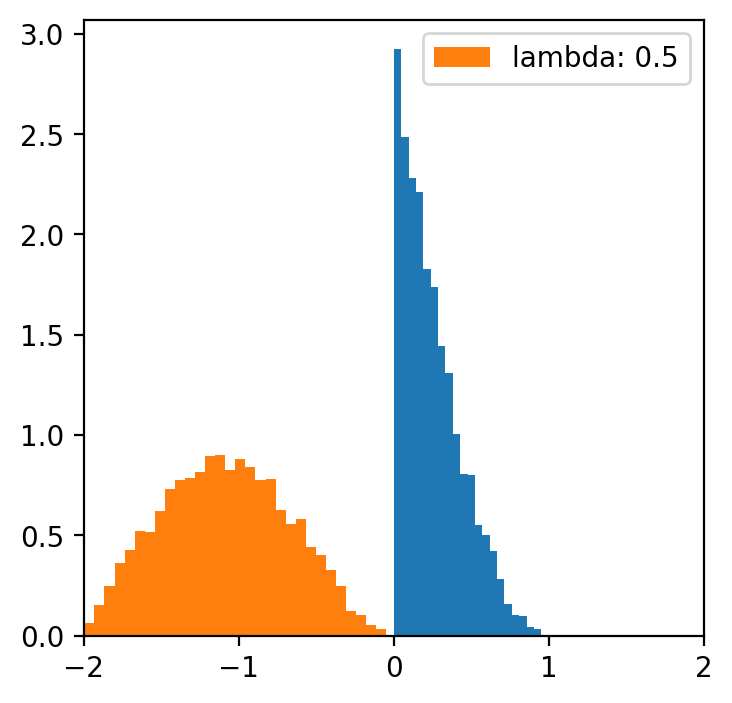
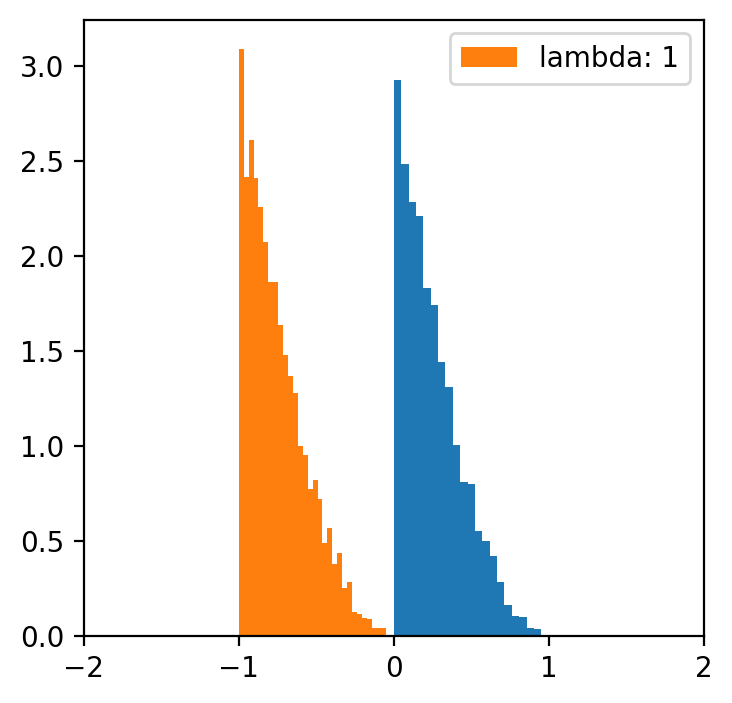
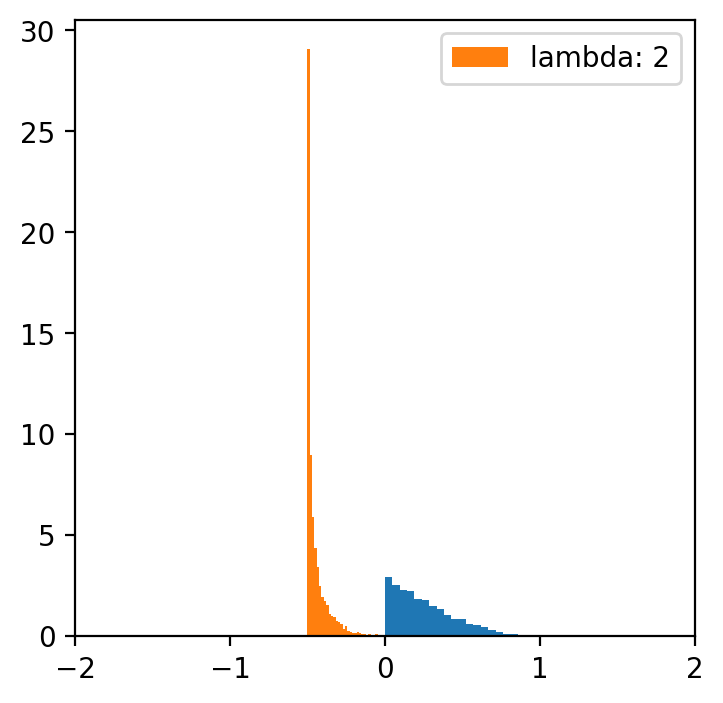
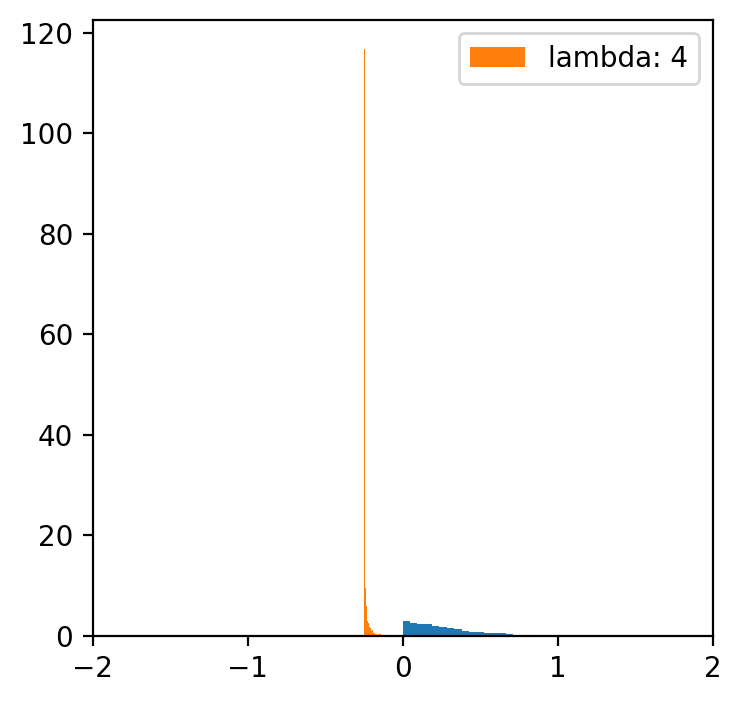
lambde = [-4,-2,-1,0.5,1,2,4] # tylko dla lambdy 0.5 mamy rozkład normalny
x = np.linspace(data.min(), data.max(), 5000)
for l in lambde:
    transformed = [(i**l -1)/l for i in data]
    plt.figure(figsize=(4,4))
    plt.hist(data, bins=20, density=True)
    plt.hist(transformed, bins=30, density=True, label = f'lambda: {l}')
    plt.xlim(-2, 2)
    plt.legend()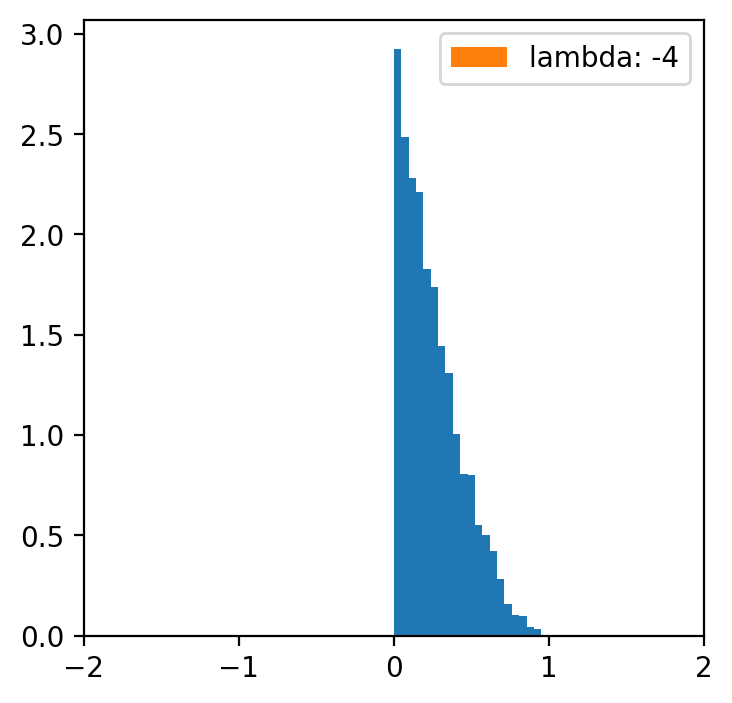

Kategoryzacja danych¶

Czasami po prostu chcielibyśmy wykonać tak zwaną procedurę „binningu”, aby móc analizować nasze dane kategorialne, porównywać kilka zmiennych kategorialnych, konstruować modele statystyczne itp. Dzięki funkcji „binning” możemy przekształcić zmienne ilościowe w kategoryczne za pomocą kilku metod:

Binning kwantylowy

Dzieli dane na grupy o równej wielkości na podstawie percentyli.
Przykład: pd.qcut(data, q=4) tworzy 4 kategorie kwantylowe.

Binning o równej szerokości kategorii

Binning w celu uzyskania stałej długości kategorii (np. co 100 USD)

\text{Bin width} = \frac{\text{max(data)} - \text{min(data)}}{\text{number of bins}}

(6)

Przykład: pd.cut(data, bins=5) tworzy 5 kategorii o równej szerokości.

Pretty Binning

Kompromis między binningiem kwantylowym a binningiem o równej szerokości, tworzący estetyczne interwały.
Zaokrąglone wartości na podstawie zakresu danych i liczby binów.

K-Means Binning

Metoda K-średnich (K-Means) to popularny algorytm grupowania (klastrowania), który dzieli dane na K grup (klastrów) na podstawie ich podobieństwa. W kontekście binningu, metoda ta pozwala na podział danych na przedziały (biny) w sposób oparty na ich naturalnym rozkładzie, a nie na sztywnych regułach, takich jak równa szerokość czy kwantyle.
Celem algorytmu K-średnich jest minimalizacja sumy kwadratów odległości punktów od ich centroidów:
$\text{Minimalizacja } \sum_{i=1}^{n} (x_i - \mu_k)^2$
(7)
gdzie $( \mu_k )$ jest średnią klastra $( k )$ .
W przypadku binningu metoda K-średnich działa następująco: dane są traktowane jako punkty w przestrzeni jednowymiarowej (np. wartości zmiennej ilościowej). Algorytm K-średnich grupuje dane w ( K ) klastrów Każdy klaster reprezentuje jeden przedział (bin), a granice przedziałów są wyznaczane na podstawie wartości centroidów.

Zalety metody K-średnich w binningu:

Dynamiczne granice: Przedziały są dostosowane do rozkładu danych, co pozwala na lepsze odwzorowanie ich struktury.
Elastyczność: Można dostosować liczbę klastrów (( K )) do potrzeb analizy.
Redukcja wpływu wartości odstających: Wartości odstające są przypisywane do klastrów, ale nie wpływają znacząco na granice innych klastrów.

Wady:

Wymaga określenia liczby klastrów (( K )): Wybór ( K ) może być trudny i wymaga eksperymentowania.
Wrażliwość na inicjalizację: Wynik może zależeć od początkowego wyboru centroidów.
Nieodporność na wartości odstające: Wartości odstające mogą wpłynąć na centroidy, jeśli są liczne.

Bag Clustering (ang. bagging, czyli bootstrap aggregating).

Grupuje dane przy użyciu technik workowych w celu poprawy stabilności klastrowania.
Klastry są tworzone poprzez agregację wyników z wielu modeli klastrowania.

Każda metoda jest odpowiednia dla różnych przypadków użycia, w zależności od dystrybucji danych i celów analizy.

Ćwiczenie Korzystając z podejścia kwantylowego, wykonaj binning zmiennej „Dochód”. Wskazówka: w Pandas mamy gotową do wykorzystania funkcję pd.qcut

dochody.head(3)
# Twój kod tutaj

Podsumowanie¶

To było wprowadzenie do data wranglingu.

Jak wspomniano, porządkowanie danych jest niezwykle ważnym tematem - i mogłoby stanowić cały przedmiot na tych studiach podyplomowych.
Ale dzisiaj skupiliśmy się na:
Identyfikacji i usuwaniu brakujących danych.
- Łączeniu zestawów danych.
- Porządkowaniu danych.
- Czyszczeniu danych.

SAD 2025

07 - Wizualizacja (zasady)

SAD 2025

09 - Statystyki opisowe

08 - Data preprocessing

W tym rozdziale¶

Czym jest data wrangling?¶

Data Wrangling z Pandas¶

Radzenie sobie z brakującymi wartościami¶

Rodzaje braków danych¶

MCAR¶

MAR¶

MNAR¶

Ładowanie zbioru danych z brakującymi wartościami¶

Dlaczego brakujące dane stanowią problem?¶

Jak radzić sobie z brakującymi danymi¶

Krok 1: Identyfikacja brakujących wartości¶

isna()¶

Sprawdzanie kolumn z nan¶

Ile nan?¶

info¶

Twoja kolej!¶

Wizualizacja brakujących wartości¶

Krok 2: Analiza rozkładu danych¶

Czy zmienna YYY jest różna w zależności od tego, czy XXX jest nan?¶

Twoja kolej!¶

Pakiet missingno¶

Znalezienie przyczyny braku danych przy użyciu wykresu macierzowego¶

Znalezienie przyczyny brakujących danych przy użyciu Heatmapy¶

Znajdowanie przyczyny braku danych przy użyciu dendrogramu¶

Krok 3: Ustal, co należy zrobić!¶

Usuwanie wszystkich wierszy z brakującymi danymi¶

Usuwanie wszystkich wierszy z brakującymi danymi w określonych kolumnach¶

Imputowanie brakujących danych¶

Imputowanie stałej wartości¶

Zgadywanie na podstawie innych cech¶

Twoja kolej!¶

Imputacja losowa / hot deck¶

Imputacja losowa Hot-deck¶

Wybór optymalnej liczby sąsiadów w metodzie k-NN - metoda łokcia¶

Wybór optymalnej liczby sąsiadów w metodzie k-NN - metoda Silhouette¶

Imputacja Hot Deck najbliższego sąsiedztwa (k-NN)¶

Podsumowanie¶

Imputacja jednowymiarowa vs. Imputacja wielowymiarowa¶

SimpleImputer¶

IterativeImputer¶

Imputacja wielokrotna¶

Zadanie domowe - do dyskusji¶

Brudne dane¶

Korekta błędów¶

Twoja kolej!¶

Duplikaty¶

Jak zidentyfikować duplikaty?¶

Duplikaty - przykład¶

Twoja kolej!¶

Łączenie zbiorów danych¶

Dlaczego scalać?¶

Jak scalać?¶

merge w praktyce¶

Ładujemy dane¶

Różne rodzaje łączenia¶

inner join¶

Twoja kolej!¶

Dlaczego merge jest tak przydatne¶

Przekształcanie danych¶

Czym są uporządkowane dane?¶

Uporządkowane vs. “nieuporządkowane” dane¶

Uporządkowane dane¶

Nieuporządkowane dane 1¶

Nieuporządkowane dane 2¶

Uporządkowanie danych¶

Zastosujmy pd.melt¶

Twoja kolej!¶

Prawdziwy zestaw danych¶

Twoja kolej!¶

Solution¶

Dlaczego uporządkowane dane są przydatne¶

Oryginalny wykres¶

Twoja kolej!¶

Transformacje danych¶

Transformacje Boxa - Coxa¶

Kategoryzacja danych¶

Podsumowanie¶

`isna()`¶

Sprawdzanie kolumn z `nan`¶

Ile `nan`?¶

`info`¶

Czy zmienna $Y$ jest różna w zależności od tego, czy $X$ jest `nan`?¶

Pakiet `missingno`¶

`merge` w praktyce¶

`inner` join¶

Dlaczego `merge` jest tak przydatne¶

Zastosujmy `pd.melt`¶