07 - Wizualizacja (zasady)

W tym rozdziale¶

Omówiliśmy już podstawy tworzenia wizualizacji danych przy użyciu pyplot i seaborn.

W tym rozdziale omówimy niektóre zasady wizualizacji danych.

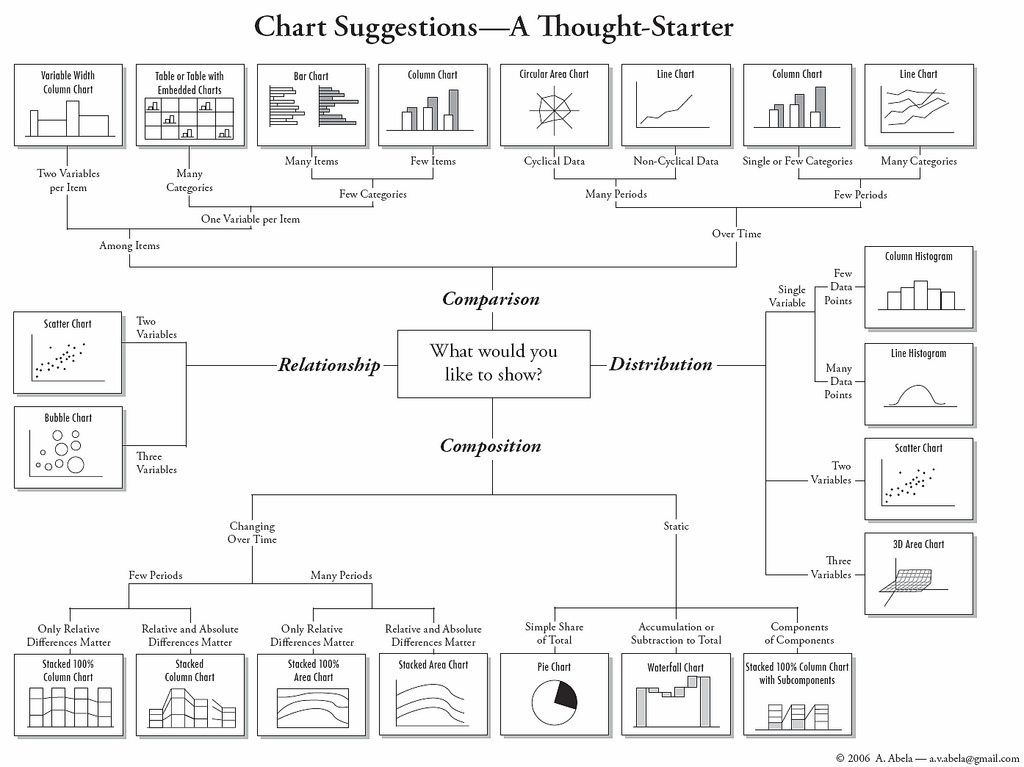
Taksonomia typów wykresów: jakiego wykresu użyć, kiedy?
- To tylko ogólny przewodnik - kontekst zawsze ma znaczenie.
Zasady i czego unikać.
Dodatkowe uwagi.

Wizualizacja danych jest niezbędną umiejętnością dla każdego analityka danych. Wybór odpowiedniego wykresu może wpłynąć na analizę lub ją zepsuć, pomagając odbiorcom w łatwym zrozumieniu spostrzeżeń.

Zrozumienie typów danych

Przed wyborem wizualizacji należy zidentyfikować typ danych, z którymi pracujemy:

Dane kategoryczne: Etykiety lub grupy (np. płeć, kategoria produktu)
Dane numeryczne: Liczby ciągłe lub dyskretne (np. wiek, przychody)
Dane szeregów czasowych: Dane indeksowane przez czas (np. ceny akcji, odczyty temperatury).
Dane relacyjne: Dane pokazujące zależności między zmiennymi (np. korelacje).

import seaborn as sns 
import pandas as pd
import matplotlib.pyplot as plt

%matplotlib inline 
%config InlineBackend.figure_format = 'retina'

Taksonomia wykresów¶

Przewodnik: którego wykresu użyć i kiedy?¶

Ile zmiennych?	Rodzaj zmiennej?	Wykres	`seaborn`
1	Ciągła	Histogram	`seaborn.histplot`
1	Kategoryczna	Count plot	`seaborn.countplot`
2	Ciągła `x`, ciągła `y`	Scatter, liniowy	`seaborn.relplot`
2	Kat. `x`, ciągła `y`	Bar, box, strip	`seaborn.catplot`

Co z $>2$ zmiennymi?¶

Zależy to od rodzaju zmiennych.

Z grubsza:

2 ciągłe, 1 kategoryczna: seaborn.relplot z hue
2 kategoryczne, 1 ciągła: seaborn.catplot z hue
3 ciągłe: seaborn.relplot z size lub hue

Zasady i czego unikać¶

W tej sekcji zaproponujemy i omówimy możliwe zasady tworzenia lepszych wizualizacji.
Wiele z tych zasad jest zależnych od kontekstu i nie bez sporów.

Ta sekcja jest ściśle wzorowana na Rozdziale 1 Wizualizacji danych Kierana Healy’ego.

Co składa się na dobrą wizualizację?¶

W The visual display of quantitative information, Edward Tufte argumentuje:

Doskonałość graficzna to dobrze zaprojektowana prezentacja interesujących danych - kwestia treści, statystyki i projektu ... [To] składa się ze złożonych pomysłów przekazanych z jasnością, precyzją i wydajnością ... [To] jest to, co daje widzowi największą liczbę pomysłów w najkrótszym czasie przy najmniejszej ilości atramentu na najmniejszej przestrzeni ... [To] jest prawie zawsze wielowymiarowe ... A doskonałość graficzna wymaga mówienia prawdy o danych. (Tufte, 1983, s. 51).

To prawda, ale także bardzo ogólna - czy możemy być bardziej konkretni?

Różne rodzaje złego wykresu?¶

Socjolog Kieran Healy wskazuje, że wykresy mogą być „złe” na różne sposoby:

Estetyczne: projekt wykresu jest estetycznie nieatrakcyjny.
Merytoryczne: albo dane, albo ich prezentacja (albo jedno i drugie) mają fundamentalne problemy.
Percepcyjne: wykres jest mylący ze względu na sposób, w jaki ludzie postrzegają i przetwarzają to, na co patrzą.

Zły gust¶

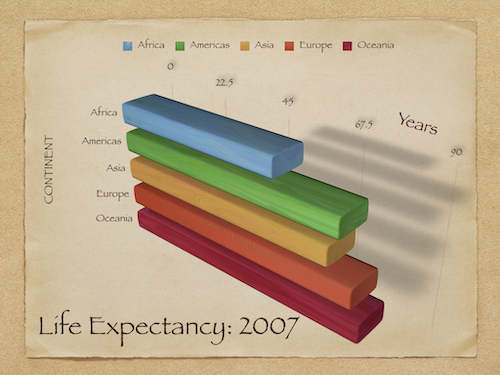
Wiele wykresów ma cechy estetyczne, które są zbyt złożone, biorąc pod uwagę to, co próbują przekazać.

Wykresy słupkowe 3D pomimo braku potrzeby stosowania trzech wymiarów.
Inne cechy estetyczne, takie jak cień.

Cechy te mogą niepotrzebnie „skomplikować” wykres, utrudniając jego interpretację.

Zbyt złożony wykres¶

Zasada 1: Maksymalizacja stosunku danych do tuszu¶

Jedną z sugestii jest maksymalizacja stosunku danych do tuszu.
Nie dodawaj elementów estetycznych, chyba że przekazują informacje.

Istnieją jednak dowody na to, że niektóre estetycznie złożone figury są łatwiejsze do zapamiętania. Więc to zależy!

Złe dane¶

Żadna ilość eleganckiej estetyki nie zrekompensuje złych danych!

Healy posługuje się przykładem wykresu z New York Times. Ten wykres jest wprowadzający w błąd:

Oś „x” sugeruje tych samych ludzi w różnym czasie, podczas gdy w rzeczywistości są to ludzie w różnym wieku w tym samym czasie.
O osi „y”: sugeruje pytanie „tak/nie”, podczas gdy jest to podzbiór odpowiedzi na 10-punktowej skali.

Zasada 2: Bądź wierny(a) danym¶

Wizualizacja powinna przedstawiać to, co mierzą dane.

(Ta zasada nie jest tak naprawdę zależna od kontekstu! Zawsze bądź wierny(a) danym).

Zła percepcja¶

Wreszcie, wykresy mogą być wprowadzające w błąd, ponieważ ich estetyka sugeruje coś nieprawidłowego na temat danych.

Wizualizacje kodują liczby za pomocą linii, kształtów i kolorów. Oznacza to, że nasza interpretacja tych kodowań jest częściowo uzależniona od tego, jak ogólnie postrzegamy kształty geometryczne i relacje. (Healy, Data Visualization).

Wykresy słupkowe i zasada proporcjonalnego atramentu¶

Kluczową cechą estetyczną wykresów słupkowych jest ilość atramentu poświęcona słupkowi.

Jako widzowie, nasze oczy mierzą względną różnicę w ilości miejsca przeznaczonego na każdy słupek.
Większe różnice percepcyjne oznaczają większe różnice wielkości.

Zasada ta może zostać naruszona na kilka sposobów.

Obcięta oś y wyolbrzymia różnice¶

Źródło: Calling Bullshit

Słupki powinny mieć jednakową szerokość¶

Źródło: Witte and Witte.

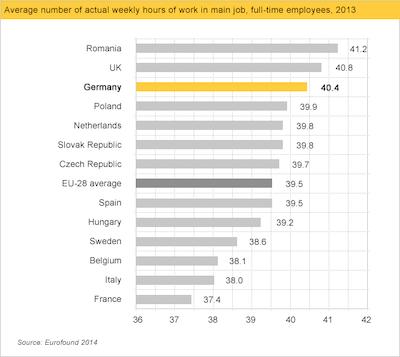
Kiedy nie zaczynać od zera?¶

Wykresy słupkowe powinny zaczynać się od zera.
Jednak w wielu przypadkach rozpoczęcie od zera może być mylące.
- W przypadku wykresów liniowych celem jest pokazanie względnej różnicy w pozycji.
- Przy bardzo dużych wartościach osi y, rozpoczęcie od zera może być mylące.

Kiedy liczy się zmiana względna (cz. 1)¶

Ten wykres pokazuje zmiany temperatury (Celsjusza) w ciągu roku i zaczyna się od 0.

import numpy as np
df_temp = pd.read_csv("data/viz/temp.csv")
# Zamiana wartości nieskończoności na NaN
df_temp = df_temp.replace([np.inf, -np.inf], np.nan)
# Usunięcie wierszy z NaN (opcjonalne, jeśli potrzebne)
df_temp = df_temp.dropna()

sns.lineplot(data=df_temp, x='Year', y='Temp_original')
plt.ylim(0)
plt.show()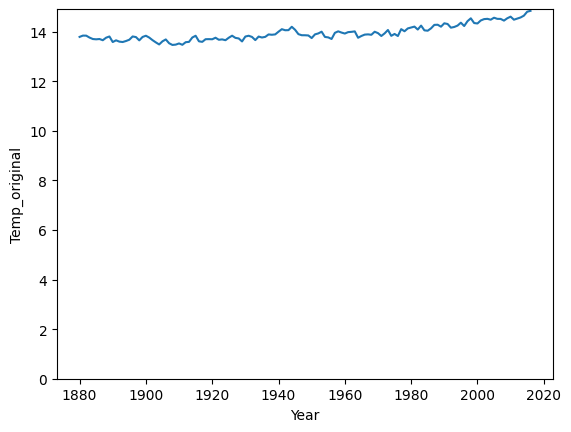

Dlaczego to ważne?

Zasada proporcjonalnego atramentu: Wykresy powinny być wierne danym i nie wprowadzać w błąd. Rozpoczęcie osi y od zera zapobiega wyolbrzymianiu różnic między wartościami.
Porównanie percepcji: Wykresy z różnymi ustawieniami osi y mogą prowadzić do różnych wniosków, co jest kluczowe w kontekście wizualizacji danych.

Kiedy liczy się zmiana względna (pkt. 2)¶

Ten wykres pokazuje zmiany temperatury (Celsjusza) w ciągu roku, ale nie zaczyna się od 0.

sns.lineplot(data = df_temp, x = 'Year', y = 'Temp_original');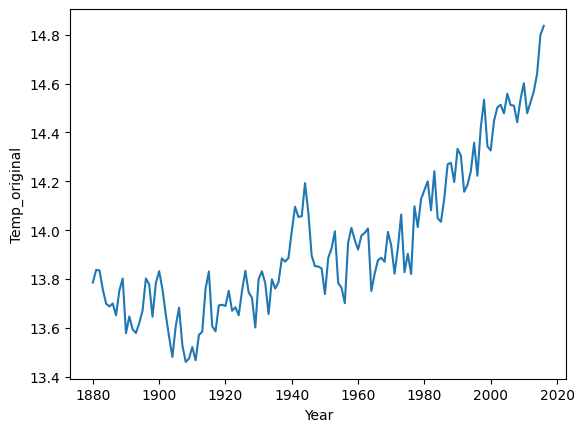

Podsumowanie: zasady i praktyka¶

Omówiliśmy kilka zasad (i odpowiadających im praktyk, których należy unikać):

Zasada 1: Maksymalizacja stosunku danych do tuszu.
Zasada 2: Wierność danym.
Zasada 3: Bądź wierny temu, co sugeruje logika wizualna wykresu.

Dodatkowe uwagi¶

Wizualizacja danych mogłaby stanowić cały kurs (lub podręcznik).

Istnieje jednak kilka innych wspólnych kwestii do omówienia:

Czy powinienem pokazać średnią (lub medianę itp.) czy surowe dane?
Czy powinienem wykluczyć wartości odstające?
Czy powinienem przekształcić moje dane (np. do skali logarytmicznej)?

Czy pokazać „surowe dane”?¶

Wszystkie miary tendencji centralnej (np. średnia, mediana) są uproszczeniem naszych danych.

Dlatego pokazanie tylko średniej „ukrywa” wiele danych.
Jeśli jednak „średnia” jest tym, na czym ci zależy, surowe dane mogą być zbyt złożone.

Osobiście staram się pokazywać surowe dane tam, gdzie to możliwe - wraz ze średnią.

Wyświetlanie zarówno podsumowania, jak i surowych danych¶

df_pokemon = pd.read_csv("data/pokemon.csv")
sns.stripplot(data = df_pokemon, x = "Legendary", y = "Attack", alpha = .2);
sns.pointplot(data = df_pokemon, x = "Legendary", y = "Attack");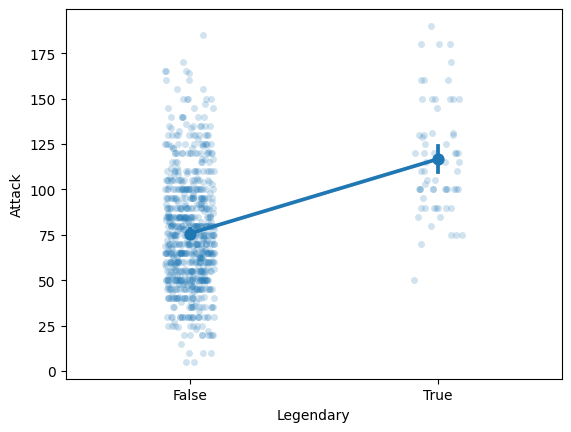

Czy wykluczyć wartości odstające?¶

Wartości odstające to punkty danych, które znacznie różnią się od innych punktów w rozkładzie.

Uwzględnienie wartości odstających w wizualizacji może być mylące.

Wydłużają one oś, mimo że nie są reprezentatywne dla danych.
Mogą odwracać uwagę od głównego punktu, który chcesz przekazać.

Czy należy je usunąć?

Przejrzystość w kwestii wykluczenia¶

Ta kwestia jest bardzo zależna od kontekstu.
Osobiście zwykle nie wykluczam wartości odstających.
Ale jeśli je wykluczasz, bądź bardzo jasny co do swojej decyzji.
- Idealnie byłoby, gdyby decyzja ta została „zarejestrowana” z wyprzedzeniem.

W kolejnych rozdziałach omówimy, jak zdefiniować/wykryć wartości odstające za pomocą z-scores.

Czy przekształcić dane?¶

Czasami „surowe” dane są mocno wypaczone.

Transformacja logarytmiczna może sprawić, że prawidłowo przekrzywione dane będą wyglądać bardziej „normalnie”.
Kiedy jest to dobry lub zły pomysł?

Dane prawoskośne mogą być mylące¶

df_gapminder = pd.read_csv("data/viz/gapminder_full.csv")
sns.histplot(data = df_gapminder, x = 'population');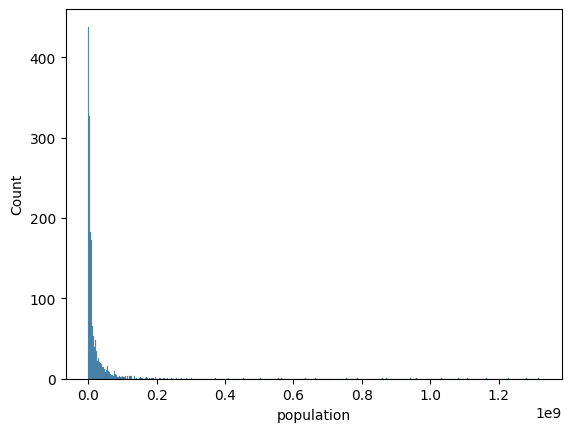

Przekształcenia logarytmiczne sprawiają, że wygląda to bardziej normalnie.¶

sns.histplot(data = df_gapminder, x = 'population', log_scale=True);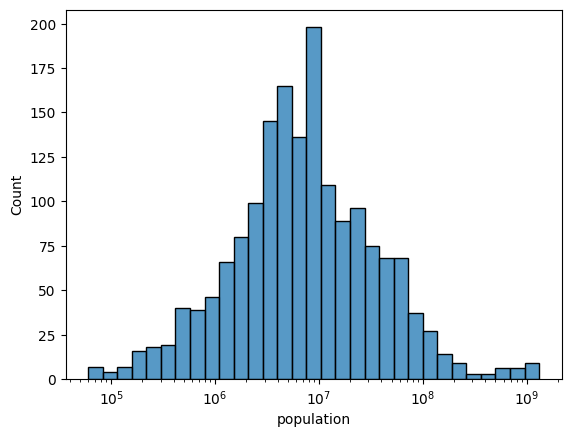

Ale co jest „prawidłowe”?¶

Rozważania, o których należy pamiętać:

Czy istnieją powody, by sądzić, że ta zmienna skaluje się logarytmicznie?
Czy istnieją powody, by sądzić, że związek tej zmiennej z innymi zmiennymi skaluje się logarytmicznie?
Czy będę prezentować tę liczbę publiczności, która rozumie skalowanie logarytmiczne?

Pod względem interpretacji:

Skala logarytmiczna implikuje wielokrotne/względne zmiany.
Skala liniowa oznacza dodatnie/absolutne zmiany.

Podsumowanie¶

Wizualizacja danych jest centralnym elementem analizy danych.

W tym rozdziale skupiliśmy się na pakietach (seaborn i pyplot), jak również na zasadach, o których należy pamiętać.

Więcej informacji można znaleźć na stronie:

SAD 2025

06 - Wizualizacja z seaborn