Univariate Analysis

Looking ahead: April Week 4, May Week 1¶

In the end of April and early May, we’ll dive deep into statistics finally.
- How do we calculate descriptive statistics in Python?
- What principles should we keep in mind?

Univariate analysis is a type of statistical analysis that involves examining the distribution and characteristics of a single variable. The prefix “uni-” means “one,” so univariate analysis focuses on one variable at a time, without considering relationships between variables.

Univariate analysis is the foundation of data analysis and is essential for understanding the basic structure of your data before moving on to more complex techniques like bivariate or multivariate analysis.

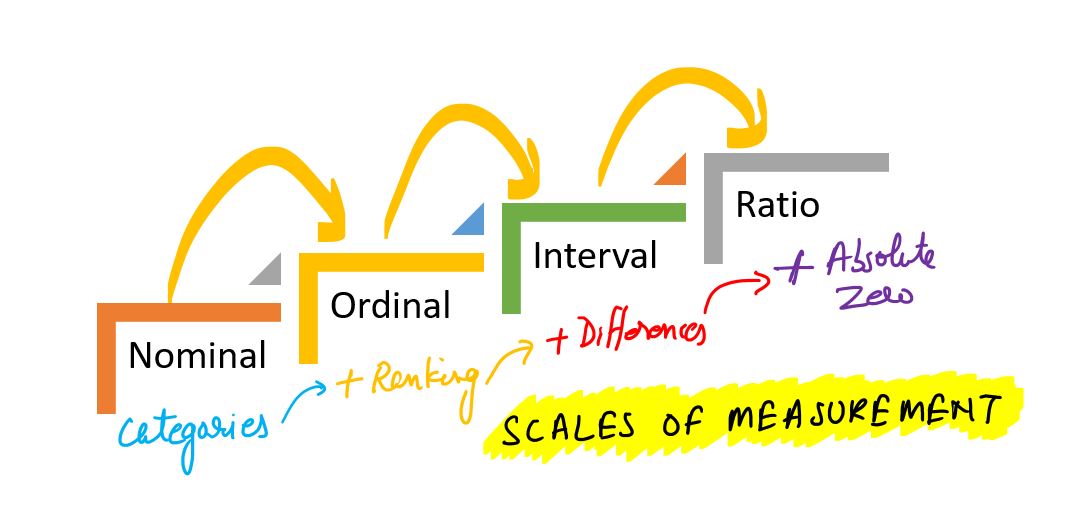
Measurement scales¶

Measurement scales determine what mathematical and statistical operations can be performed on data. There are four basic types of scales:

Nominal scale

Data is used only for naming or categorizing.
The order between values cannot be determined.
Possible operations: count, mode, frequency analysis.

Examples:

Pokémon type (type_1): “fire”, ‘water’, ‘grass’, etc.
Species, gender, colors, brands etc.

import pandas as pd
df_pokemon = pd.read_csv("data/pokemon.csv")
df_pokemon["Type 1"].value_counts()

Type 1
Water       112
Normal       98
Grass        70
Bug          69
Psychic      57
Fire         52
Electric     44
Rock         44
Dragon       32
Ground       32
Ghost        32
Dark         31
Poison       28
Steel        27
Fighting     27
Ice          24
Fairy        17
Flying        4
Name: count, dtype: int64

Ordinal scale

Data can be ordered, but the distances between them are not known.
Possible operations: median, quantiles, rank tests (e.g. Spearman).

Examples:

Strength level: “low”, “medium”, “high”.
Quality ratings: “weak”, “good”, “very good”.

import seaborn as sns

titanic = sns.load_dataset("titanic")

print(titanic["class"].unique())

['Third', 'First', 'Second']
Categories (3, object): ['First', 'Second', 'Third']

Interval scale

The data is numerical, with equal intervals, but lacks an absolute zero.
Differences, mean, and standard deviation can be calculated.
Ratios (e.g., “twice as much”) do not make sense.

Examples:

Temperature in °C (but not in Kelvin!). Why? There is no absolute zero—zero does not mean the absence of the property; it is just a conventional reference point. 0°C does not mean no temperature; 20°C is not 2 × 10°C.
Year in a calendar (e.g., 1990). Why? Year 0 does not mark the beginning of time; 2000 is not 2 × 1000.
Time in the hourly system (e.g., 13:00). Why? 0:00 does not mean no time, but rather an established reference point.

Ratio scale

Numerical data with an absolute zero.
All mathematical operations, including division, can be performed.

Not all numerical data is on a ratio scale! For example, temperature in degrees Celsius is not on a ratio scale because 0°C does not mean the absence of temperature. However, temperature in Kelvin (K) is, as 0 K represents the absolute absence of thermal energy.

Examples:

Height, weight, number of Pokémon attack points (attack), HP, speed.

df_pokemon[["HP", "Attack", "Speed"]].describe()

Table: Measurement scales in statistics¶

Scale	Example	Is it possible to order?	Equal spacing?	Absolute zero?	Sample statistical calculations
Nominal	Pokémon type (`fire`, `water` etc.)	❌	❌	❌	Mode, counts, frequency analysis
Ordinal	Ticket class (`First`, `Second`, `Third`)	✅	❌	❌	Median, quantiles
Interval	Temperature in °C	✅	✅	❌	Mean, standard deviation
Ratio	HP, attack, height	✅	✅	✅	All mathematical operations/statistical

Conclusion: The type of scale affects the choice of statistical methods - for example, the Pearson correlation test requires quotient or interval data, while the Chi² test requires nominal data.

Quiz: measurement scales in statistics.¶

Answer the following questions by choosing one correct answer. You will find the solutions at the end.

1. Which scale enables ordering of data, but does not have equal spacing?¶

A) Nominal
B) Ordinal
C) Interval
D) Ratio

2. An example of a variable on the nominal scale is:¶

A) Temperature in °C
B) Height
C) Type of Pokémon (fire, grass, water)
D) Satisfaction level (low, medium, high).

3. Which scale does not have absolute zero, but has equal spacing?¶

A) Ratio
B) Ordinal
C) Interval
D) Nominal

4. What operations are allowed on variables on an ordinal scale?¶

A) Mean and standard deviation
B) Mode and Pearson correlation
C) Median and rank tests
D) Quotients and logarithms

5. The variable `“class”` in the Titanic set (`First`, `Second`, `Third`) is an example:¶

A) Nominal scale
B) Ratio scale
C) Interval scale
D) Ordinal scale

Descriptive statistics¶

Descriptive statistics deals with the description of the distribution of data in a sample. Descriptive statistics give us basic summary measures about a set of data. Summary measures include measures of central tendency (mean, median and mode) and measures of variability (variance, standard deviation, minimum/maximum values, IQR (interquartile range), skewness and kurtosis).

This week¶

Now we’re going to look at describing our data - as well as the basics of statistics.

There are many ways to describe a distribution.

Here we will discuss:

Measures of central tendency: what is the typical value in this distribution?
Measures of variability: how much do the values differ from each other?
Measures of skewness: how strong is the asymmetry of the distribution?
Measures of curvature: what is the intensity of extreme values?

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns 
import scipy.stats as stats

%matplotlib inline 
%config InlineBackend.figure_format = 'retina'

Central tendency¶

The central tendency refers to the “typical value” in a distribution.

The central tendency refers to the central value that describes the distribution of a variable. It can also be referred to as the center or location of the distribution. The most common measures of central tendency are average, median and mode. The most common measure of central tendency is the mean. In the case of skewed distributions or when there is concern about outliers, the median may be preferred. The median is thus a more reliable measure than the mean.

There are many ways to measure what is “typical” - average:

Arithmetic mean
Median (middle value)
Mode (dominant)

Why is this useful?¶

A dataset may contain many observations.
- For example, $N$ = 5000 of survey responses regarding `height’.
One way to “describe” this distribution is to visualize it.
But it is also helpful to reduce this distribution to a single number.

This is necessarily a simplification of our dataset!

Arithmetic average¶

Arithmetic average is defined as the sum of all values in a distribution, divided by the number of observations in that distribution.

numbers = [1, 2, 3, 4]
### calculating manually...
sum(numbers)/len(numbers)

2.5

The most common measure of central tendency is the average.
The mean is also known as the simple average.
It is denoted by the Greek letter $µ$ for a population and $\bar{x}$ for a sample.
We can find the average of the number of elements by adding all the elements in the data set and then dividing by the number of elements in the data set.
This is the most popular measure of central tendency, but it has a drawback.
The average is affected by the presence of outliers.
Thus, the average alone is not sufficient for making business decisions.

\bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i

(1)

`numpy.mean`¶

The numpy package has a function that calculates an average on a list or numpy.ndarray.

np.mean(numbers)

np.float64(2.5)

`scipy.stats.tmean`¶

The scipy.stats library has a variety of statistical functions.

stats.tmean(numbers)

np.float64(2.5)

Calculating the `average` of a `pandas` column.¶

If we work with DataFrame, we can calculate the average of specific columns.

import pandas as pd
df_gapminder = pd.read_csv("data/gapminder_full.csv")
df_gapminder.head(2)

df_gapminder['life_exp'].mean()

np.float64(59.474439366197174)

Your turn¶

How to calculate the mean life expectancy for EUROPEan countries (2007).

### Your code here

Average and skewness¶

Skewness means that there are values extending one of the “tails” of the distribution.

Of the measures of central tendency, “average” is the most dependent on the direction of skewness.

How would you describe the following skewness?
Do you think the “mean” would be higher or lower than the “median”?

sns.histplot(data = df_gapminder, x = "gdp_cap")
plt.axvline(df_gapminder['gdp_cap'].mean(), linestyle = "dotted");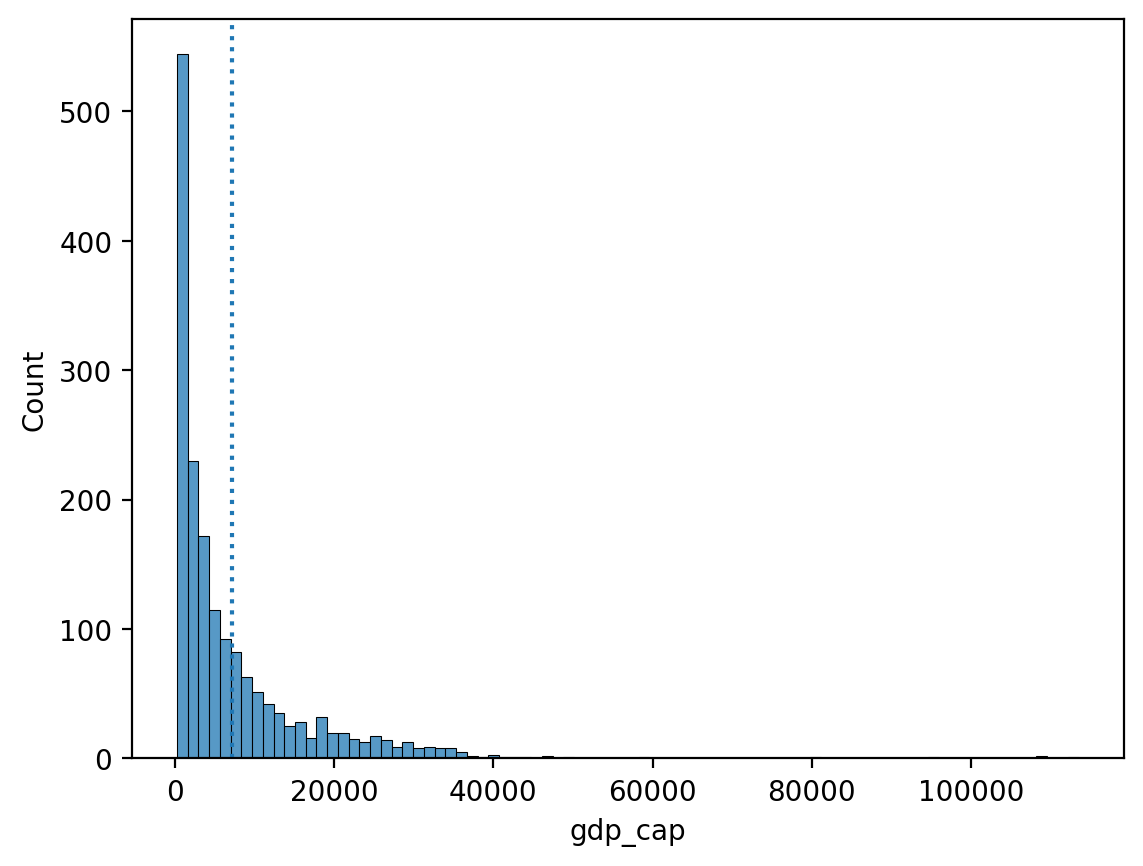

Your turn¶

Is it possible to calculate the average of the column “continent”? Why or why not?

### Your comment here

Your turn¶

Subtract each observation in numbers from the average of this list.
Then calculate the sum of these deviations from the average.

What is their sum?

numbers = np.array([1, 2, 3, 4])
### Your code here

Summary of the first part¶

The mean is one of the most common measures of central tendency.
It can only be used for continuous interval/ratio data.
The sum of deviations from the mean is equal to 0.
The “mean” is most affected by skewness and outliers.

Median¶

Median is calculated by sorting all values from smallest to largest and then finding the value in the middle.

The median is the number that divides a data set into two equal halves.
To calculate the median, we need to sort our data set of n numbers in ascending order.
The median of this data set is the number in the position $(n+1)/2$ if $n$ is odd.
If n is even, the median is the average of the $(n/2)$ third number and the $(n+2)/2$ third number.
The median is robust to outliers.
Thus, in the case of skewed distributions or when there is concern about outliers, the median may be preferred.

df_gapminder['gdp_cap'].median()

np.float64(3531.8469885)

Comparison of `median` and `average`.¶

The direction of inclination has less effect on the median.

sns.histplot(data = df_gapminder, x = "gdp_cap")
plt.axvline(df_gapminder['gdp_cap'].mean(), linestyle = "dotted", color = "blue")
plt.axvline(df_gapminder['gdp_cap'].median(), linestyle = "dashed", color = "red");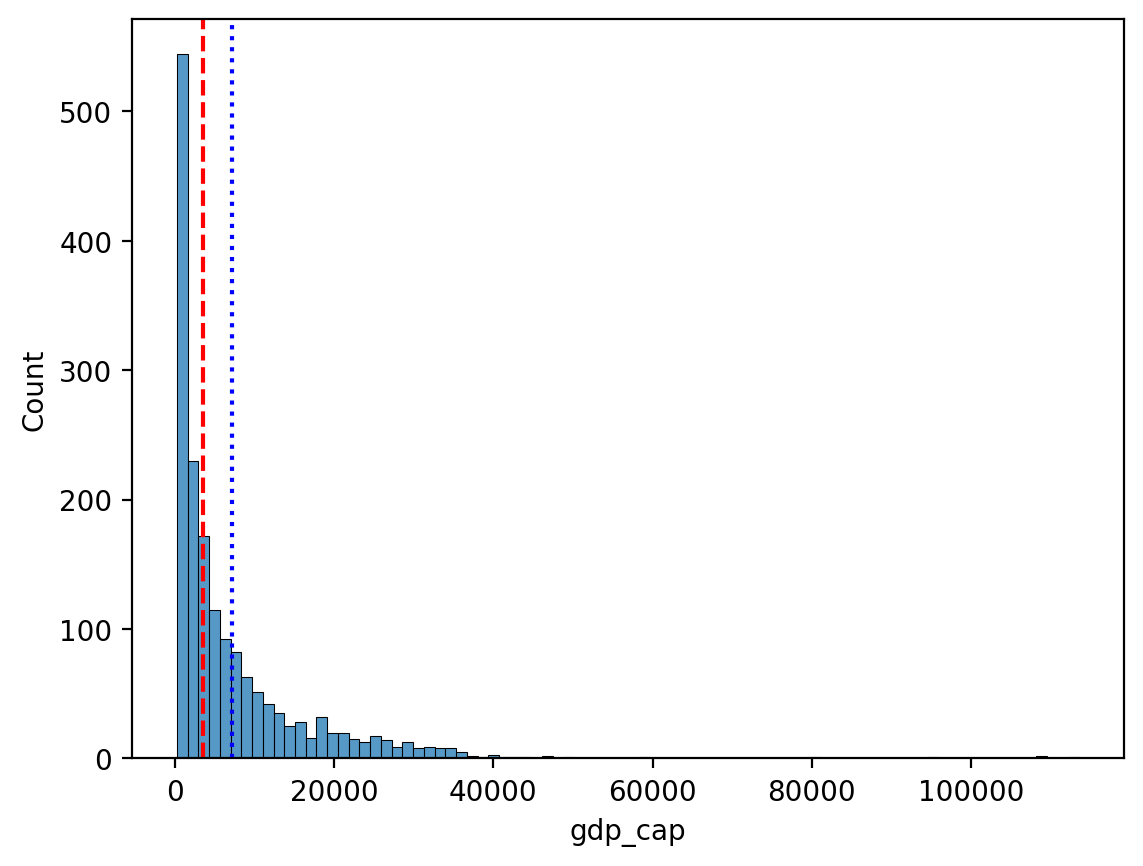

Your turn¶

Is it possible to calculate the median of the column “continent”? Why or why not?

### Your comment here

Mode¶

Mode is the most common value in a data set.

Unlike median or average, mode can be used with categorical data.

df_pokemon = pd.read_csv("data/pokemon.csv")
df_pokemon['Type 1'].mode()

0    Water
Name: Type 1, dtype: object

`mode()` returns multiple values?¶

If multiple values bind for the most frequent one, mode() will return them all.
This is because technically, a distribution can have multiple values for the most frequent - modal!

df_gapminder['gdp_cap'].mode()

0          241.165876
1          277.551859
2          298.846212
3          299.850319
4          312.188423
            ...      
1699     80894.883260
1700     95458.111760
1701    108382.352900
1702    109347.867000
1703    113523.132900
Name: gdp_cap, Length: 1704, dtype: float64

Measures of central tendency - summary¶

Measure	Can be used for:	Limitations
Mean	Continuous data	Influence on skewness and outliers
Median	Continuous data	Does not include the value of all data points in the calculation (ranks only)
Mode	Continuous and categorical data	Considers only frequent; ignores other values

Quantiles¶

Quantiles are descriptive - positional statistics that divide an ordered data set into equal parts. The most common quantiles are:

Median (quantile of order 0.5),
Quartiles (divide the data into 4 parts),
Deciles (into 10 parts),
Percentiles (into 100 parts).

Definition¶

A quantile of order $q \in (0,1)$ is a value of $x_q$ such that:

P(X \leq x_q) = q

(2)

In other words: $q \cdot 100\%$ of the values in the data set are less than or equal to $x_q$ .

Formula (for an ordered data set)¶

For a data sample $x_1, x_2, \ldots, x_n$ ordered in ascending order, the quantile of order $q$ is determined as:

Calculate the positional index:

i = q \cdot (n + 1)

(3)

If $i$ is an integer, then the quantile is $x_i$ .
If $i$ is not integer, we interpolate linearly between adjacent values:

x_q = x_{\lfloor i \rfloor} + (i - \lfloor i \rfloor) \cdot (x_{\lceil i \rceil} - x_{\lfloor i \rfloor})

(4)

Note: In practice, different methods are used to determine quantiles - libraries such as NumPy or Pandas have different modes (e.g. method='linear', method='midpoint').

Example - we calculate step by step:¶

For data: $[3, 7, 8, 5, 12, 14, 21, 13, 18]$

We arrange the data in ascending order:

$[3, 5, 7, 8, 12, 13, 14, 18, 21]$

Median (quantile of order 0.5):

The number of elements $n = 9$ , the middle element is the 5th value:

$\text{Median} = x_5 = 12$

First quartile (Q1, quantile of order 0.25):

$i = 0.25 \cdot (9 + 1) = 2.5$

Interpolation between $x_2 = 5$ and $x_3 = 7$ :

$Q_1 = 5 + 0.5 \cdot (7 - 5) = 6$

Third quartile (Q3, quantile of 0.75):

$i = 0.75 \cdot 10 = 7.5$

Interpolation between $x_7 = 14$ and $x_8 = 18$ :

$Q_3 = 14 + 0.5 \cdot (18 - 14) = 16$

Deciles¶

Deciles divide data into 10 equal parts. For example:

D1 is the 10th percentile (quantile of 0.1),
D5 is the median (0.5),
D9 is the 90th percentile (0.9).

The formula is the same as for overall quantiles, just use the corresponding $q$ . E.g. for D3:

$q = \frac{3}{10} = 0.3$

Percentiles¶

Percentiles divide data into 100 equal parts. E.g.:

P25 = Q1,
P50 = median,
P75 = Q3,
P90 is the value below which 90% of the data is.

With percentiles, we can better understand the distribution of data - for example, in standardized tests, a score is often given as a percentile (e.g., “85th percentile” means that someone scored better than 85% of the population).

Quantiles - summary¶

Name	Symbol	Quantile ( q )	Meaning
Q1	Q1	0.25	25% of data ≤ Q1
Median	Q2	0.5	50% of data ≤ Median
Q3	Q3	0.75	75% of data ≤ Q3
Decile 1	D1	0.1	10% of data ≤ D1
Decile 9	D9	0.9	90% of data ≤ D9
Percentile 95	P95	0.95	95% of data ≤ P95

Example - calculations of quantiles¶

# Sample data
mydata = [3, 7, 8, 5, 12, 14, 21, 13, 18]
mydata_sorted = sorted(mydata)
print("Sorted data:", mydata_sorted)

Sorted data: [3, 5, 7, 8, 12, 13, 14, 18, 21]

# Conversion to Pandas Series
s = pd.Series(mydata)

# Quantiles
q1 = s.quantile(0.25) # lower quartile Q1
median = s.quantile(0.5) # median or middle quartile Q2 = Me
q3 = s.quantile(0.75) # upper quartile Q3

# Deciles
d1 = s.quantile(0.1) # bottom 10% of data...
d9 = s.quantile(0.9) # top 10% of data...

# Percentiles
p95 = s.quantile(0.95)  # top 5% of data...

print("Quantiles:")
print(f"Q1 (25%): {q1}")
print(f"Median (50%): {median}")
print(f"Q3 (75%): {q3}")
print("\nDeciles:")
print(f"D1 (10%): {d1}")
print(f"D9 (90%): {d9}")
print("\nPercentiles:")
print(f"P95 (95%): {p95}")

Quantiles:
Q1 (25%): 7.0
Median (50%): 12.0
Q3 (75%): 14.0

Deciles:
D1 (10%): 4.6
D9 (90%): 18.6

Percentiles:
P95 (95%): 19.799999999999997

# Create boxplot
fig, ax = plt.subplots(figsize=(8, 6))–
sns.boxplot(data=mydata, ax=ax, color='lightblue', width=0.3)

# Calculate statistics
minimum = np.min(mydata)
q1 = np.percentile(mydata, 25)
median = np.median(mydata)
q3 = np.percentile(mydata, 75)
maximum = np.max(mydata)
mean = np.mean(mydata)

ax.scatter(0, minimum, color='red', label='Min', zorder=5)
ax.scatter(0, q1, color='orange', label='Q1 (25th percentile)', zorder=5)
ax.scatter(0, median, color='green', label='Median (50th percentile)', zorder=5)
ax.scatter(0, q3, color='purple', label='Q3 (75th percentile)', zorder=5)
ax.scatter(0, maximum, color='brown', label='Max', zorder=5)
ax.scatter(0, mean, color='black', marker='D', s=60, label='Mean', zorder=5)

for value, name, color in zip(
    [minimum, q1, median, mean, q3, maximum],
    ['Min', 'Q1', 'Median', 'Mean', 'Q3', 'Max'],
    ['red', 'orange', 'green', 'black', 'purple', 'brown']
):
    ax.text(0.1, value, f'{name}: {value:.2f}', verticalalignment='center', color=color)


ax.set_title('Boxplot of mydata with All Measures Marked')
ax.legend(bbox_to_anchor=(1.05, 1), loc='upper left')
plt.show()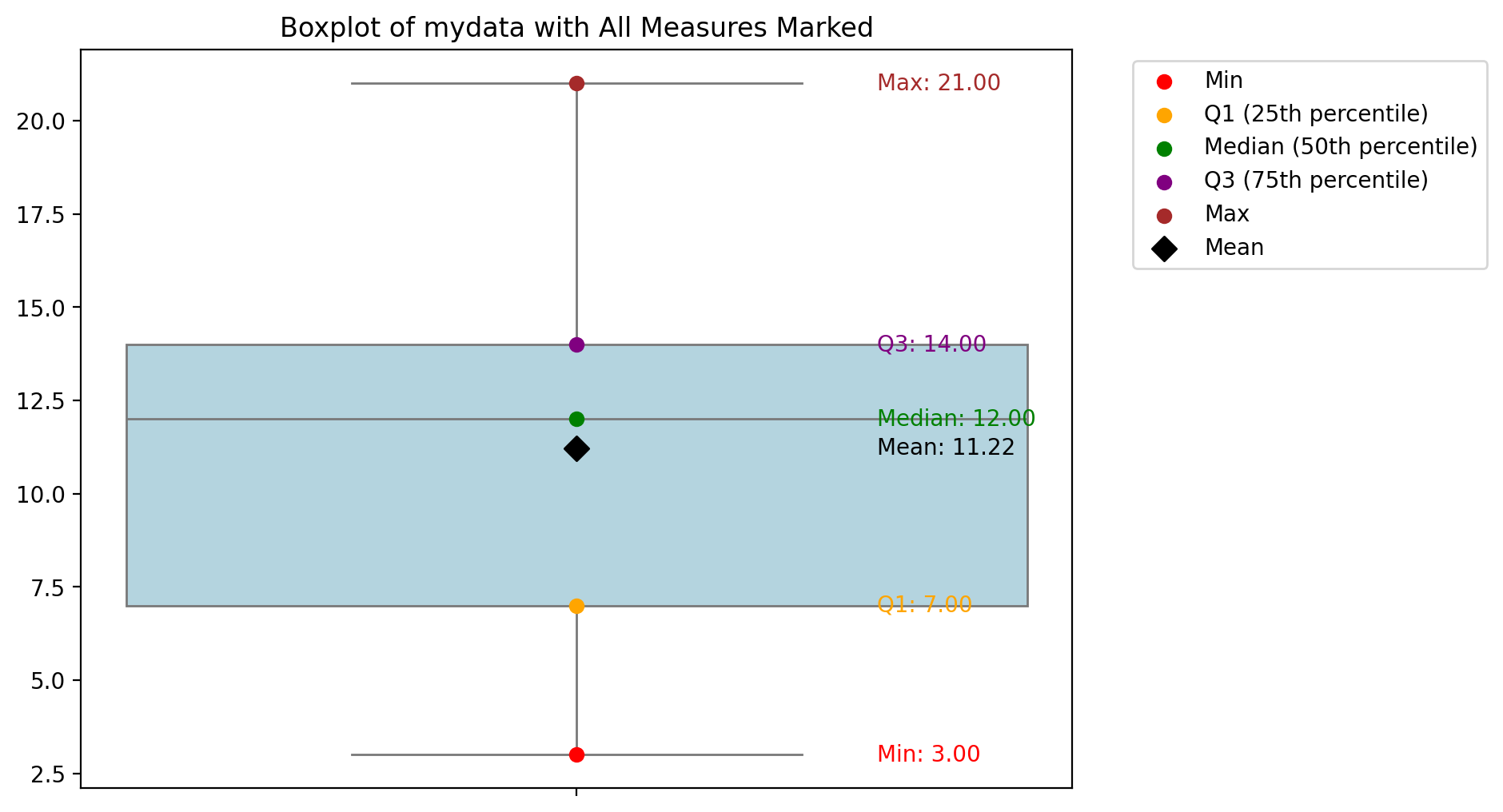

Your turn!¶

Try to change the boxplot into the violin plot (or add it).

Looking at the aforementioned quantile results and the box plot, try to interpret these measures.

Variability¶

Variability (or dispersion) refers to the degree to which values in a distribution are dispersed, i.e., differ from each other.

The dispersion is an indicator of how far from the center we can find data values. The most common measures of dispersion are variance, standard deviation and interquartile range (IQR). The variance is a standard measure of dispersion. The standard deviation is the square root of the variance. The variance and standard deviation are two useful measures of scatter.

The `mean` hides the variance!¶

Both distributions have the same mean, but different standard deviations.

### Let's create some distributions
d1 = np.random.normal(loc = 0, scale = 1, size = 1000)
d2 = np.random.normal(loc = 0, scale = 5, size = 1000)
### Plots
fig, axes = plt.subplots(1, 2, sharex=True, sharey=True);
p1 = axes[0].hist(d1, alpha = .5)
p2 = axes[1].hist(d2, alpha = .5)
axes[0].set_title("Lower variance");
axes[1].set_title("Higher variance");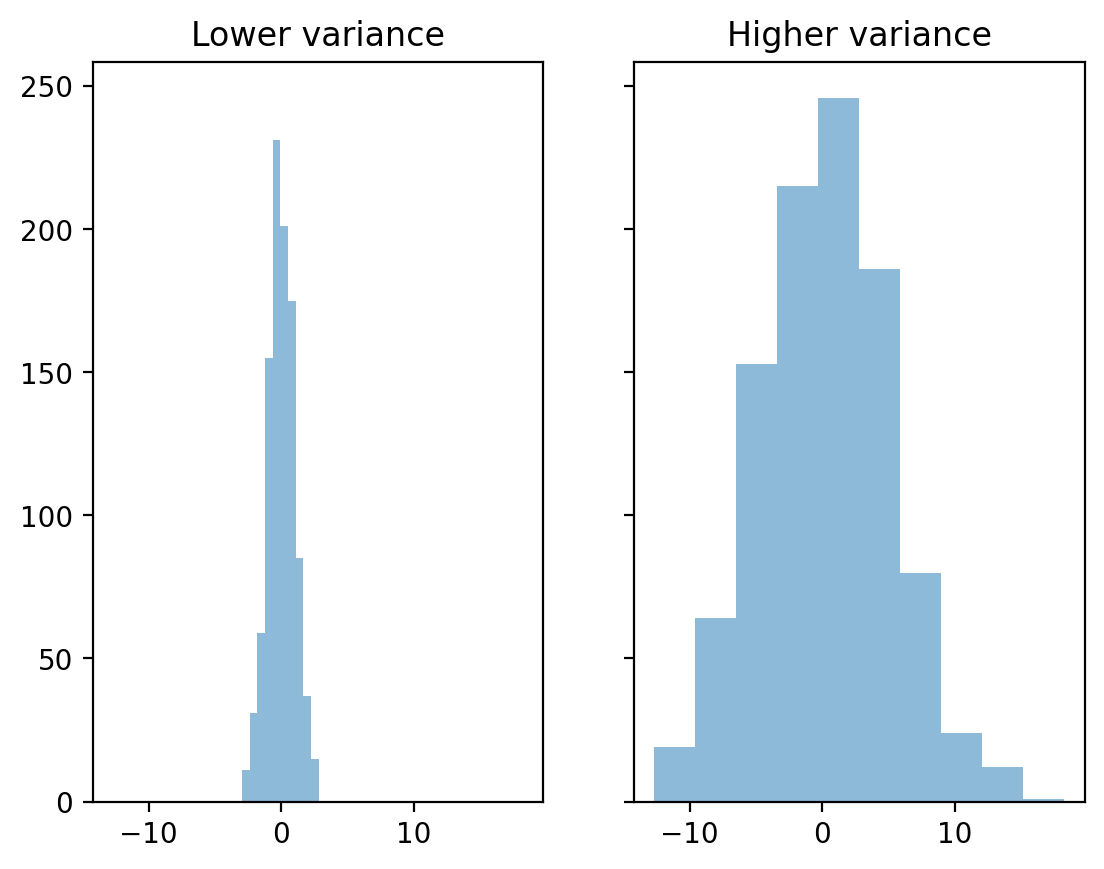

Volatility detection¶

There are at least three main approaches to quantifying variability:

Range: the difference between the “maximum” and “minimum” value.
Interquartile range (IQR): The range of the middle 50% of the data.
Variance and Standard Deviation: the typical value by which results deviate from the mean.

Range¶

Range Is the difference between the maximum and minimum values.

Intuitive, but only considers two values in the entire distribution.

d1.max() - d1.min()

np.float64(5.773802970965855)

d2.max() - d2.min()

np.float64(30.896869694831192)

IQR¶

The interquartile range (IQR) is the difference between a value in the 75% percentile and a value in the 25% percentile.

It focuses on the center 50%, but still only considers two values.

IQR is calculated using the limits of the data between the 1st and 3rd quartiles.
The interquartile range (IQR) can be calculated as follows: $IQR = Q3 - Q1$
In the same way that the median is more robust than the mean, the IQR is a more robust measure of scatter than the variance and standard deviation and should therefore be preferred for small or asymmetric distributions.
It is a robust measure of scatter.

## Let's calculate quantiles - quartiles Q1 and Q3
q3, q1 = np.percentile(d1, [75 ,25])
q3 - q1

np.float64(1.345875103819967)

## Let's calculate quantiles - quartiles Q1 and Q3
q3, q1 = np.percentile(d2, [75 ,25])
q3 - q1

np.float64(6.6243520774932)

Variance and standard deviation.¶

The Variance measures the dispersion of a set of data points around their mean value. It is the average of the squares of the individual deviations. The variance gives the results in original units squared.

s^2 = \frac{1}{n - 1} \sum_{i=1}^{n} (x_i - \bar{x})^2

(5)

Standard deviation (SD) measures the typical value by which the results in the distribution deviate from the mean.

s = \sqrt{s^2} = \sqrt{\frac{1}{n - 1} \sum_{i=1}^{n} (x_i - \bar{x})^2}

(6)

where: - $n$ - the number of elements in the sample - $\bar{x}$ - the arithmetic mean of the sample

What to keep in mind:

SD is the square root of variance.
There are actually two measures of SD:
SD of a population: when you measure the entire population of interest (very rare).
- SD of a sample: when you measure a sample (typical case); we’ll focus on that.

SD, explained¶

First, calculate the total square deviation.
- What is the total square deviation from the “mean”?
Then divide by n - 1: normalize to the number of observations.
- What is the average squared deviation from the `average’?
Finally, take the square root:
- What is the average deviation from the “mean”?

The standard deviation represents the typical or “average” deviation from the “mean”.

SD calculation in `pandas`¶

df_pokemon['Attack'].std()

np.float64(32.45736586949845)

df_pokemon['HP'].std()

np.float64(25.53466903233207)

Note on `numpy.std`!!!¶

By default, numpy.std calculates the population standard deviation!
You need to modify the ddof parameter to calculate the sample standard deviation.

This is a very common error.

### SD in population
d1.std()

np.float64(1.0006452408451578)

### SD for sample
d1.std(ddof = 1)

np.float64(1.001145939020521)

Coefficient of variation (CV).¶

The coefficient of variation (CV) is equal to the standard deviation divided by the mean.
It is also known as “relative standard deviation.”

CV = \frac{s}{\bar{x}} \cdot 100%

(7)

X = [2, 4, 4, 4, 5, 5, 7, 9]
mean = np.mean(X)

# Variance and standard deviation from scipy (for the sample!):
var_sample = stats.tvar(X)      # sample variance
std_sample = stats.tstd(X)      # sample sd

# CV (for sample):
cv_sample = (std_sample / mean) * 100

print(f"Mean: {mean}")
print(f"Sample variance (scipy): {var_sample}")
print(f"Sample sd (scipy): {std_sample}")
print(f"CV (scipy): {cv_sample:.2f}%")

Mean: 5.0
Sample variance (scipy): 4.571428571428571
Sample sd (scipy): 2.138089935299395
CV (scipy): 42.76%

Interquartile deviation¶

Interquartile deviation (sometimes called the semi-interquartile range) is defined as half of the interquartile range:

\text{IQR deviation} = \frac{Q3 - Q1}{2}

(8)

This value shows the average distance from the median to the quartiles and is a robust measure of variability.

A small interquartile deviation means the middle 50% of the data are close to the median.
A large interquartile deviation means the middle 50% are more spread out.

It is less sensitive to outliers than the standard deviation or range!

Your turn!¶

Calculate STD and CV for the SPEED of LEGENDARY and NOT LEGENDARY pokemons. What is the IQR deviation?

# Your code here!

Measures of the shape of the distribution¶

Now we will look at measures of the shape of the distribution. There are two statistical measures that can tell us about the shape of a distribution. These are skewness and curvature. These measures can be used to tell us about the shape of the distribution of a data set.

Skewness¶

Skewness is a measure of the symmetry of a distribution, or more precisely, the lack of symmetry.
It is used to determine the lack of symmetry with respect to the mean of a data set.
It is a characteristic of deviation from the mean.
It is used to indicate the shape of a data distribution.

Skewness is a measure of the asymmetry of the distribution of data relative to the mean. It tells us whether the data are more ‘stretched’ to one side.

Interpretation:

Skewness > 0 - right-tailed (positive): long tail on the right (larger values are more dispersed)
Skewness < 0 - left (negative): long tail on the left (smaller values are more dispersed)
Skewness ≈ 0 - symmetric distribution (e.g. normal distribution)

Formula (for the sample):

A = \frac{n}{(n-1)(n-2)} \sum_{i=1}^{n} \left( \frac{x_i - \bar{x}}{s} \right)^3

(9)

where:

$n$ - number of observations
$\bar{x}$ - sample mean
$s$ - standard deviation of the sample

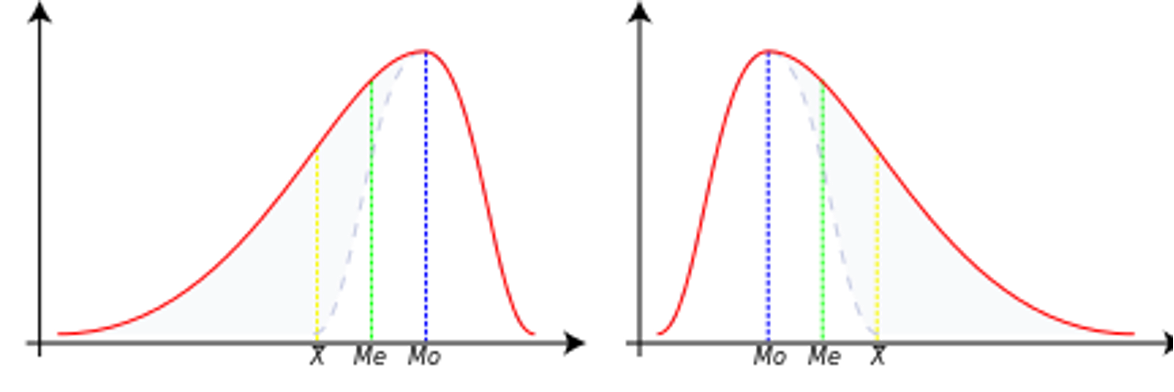
Negative skewness¶

In this case, the data are skewed or shifted to the left.
By skewed to the left, we mean that the left tail is long relative to the right tail.
The data values may extend further to the left, but are concentrated on the right.
So we are dealing with a long tail, and the distortion is caused by very small values that pull the mean down and it is smaller than the median.
In this case we have Mean < Median < Mode.

Zero skewness¶

This means that the dataset is symmetric.
A dataset is symmetric if it looks the same to the left and right of the midpoint.
A dataset is bell-shaped or symmetric.
A perfectly symmetrical dataset will have a skewness of zero.
So a normal distribution that is perfectly symmetric has a skewness of 0.
In this case we have Mean = Median = Mode.

Positive skewness¶

The dataset is skewed or shifted to the right.
By skewed to the right we mean that the right tail is long relative to the left tail.
The data values are concentrated on the right side.
There is a long tail on the right side, which is caused by very large values that pull the mean upwards and it is larger than the median.
So we have Mean > Median > Mode.

from scipy.stats import skew
X = [2, 4, 4, 4, 5, 5, 7, 9]
skewness = skew(X)
print(f"Skewness of X: {skewness:.4f}")

Skewness of X: 0.6562

Your turn¶

Try to interpret the above-mentioned result and calculate example slant ratios for several groups of Pokémon.

# Your comment here

Interquartile Skewness¶

IQR skewness is a robust, non-parametric measure of skewness that uses the positions of the quartiles rather than the mean and standard deviation. It is particularly useful for detecting asymmetry in data distributions, especially when outliers are present.

The formula for IQR Skewness is:

IQR\ Skewness = \frac{(Q3 - Median) - (Median - Q1)}{Q3 - Q1}

(10)

This method is less sensitive to outliers and more robust than moment-based skewness, making it ideal for exploratory data analysis.

Your turn¶

Try to calculate the IQR Skewness coefficient for the sample data:

mydata = [3, 7, 8, 5, 12, 14, 21, 13, 18]
# Your code here

Kurtosis¶

Contrary to what some textbooks claim, kurtosis does not measure the ‘flattening’, the ‘peaking’ of a distribution.

Kurtosis depends on the intensity of the extremes, so it measures what happens in the ‘tails’ of the distribution, the shape of the ‘top’ is irrelevant!

Excess kurtosis is just kurtosis minus 3. It’s used to compare a distribution to the normal distribution (which has kurtosis = 3).

Sample kurtosis:

\text{Kurtosis} = \frac{1}{n} \sum_{i=1}^{n} \left( \frac{x_i - \bar{x}}{s} \right)^4

(11)

\text{Normalized kurtosis} = \text{Kurtosis} - 3

(12)

Reference range for kurtosis¶

The reference standard is the normal distribution, which has a kurtosis of 3.
Often Excess is presented instead of kurtosis, where excess is simply Kurtosis - 3.

Mesocurve¶

A normal distribution has a kurtosis of exactly 3 (Excess exactly 0).
Any distribution with kurtosis $≈3$ (exces ≈ 0) is called mezocurtic.

Platykurtic curve¶

A distribution with kurtosis $<3$ (Excess < 0) is called platykurtic.
Compared to a normal distribution, its central peak is lower and wider and its tails are shorter and thinner.

Leptokurtic curve¶

A distribution with kurtosis $>3$ (Excess > 0) is called leptocurtic.
Compared to a normal distribution, its central peak is higher and sharper and its tails are longer and thicker.

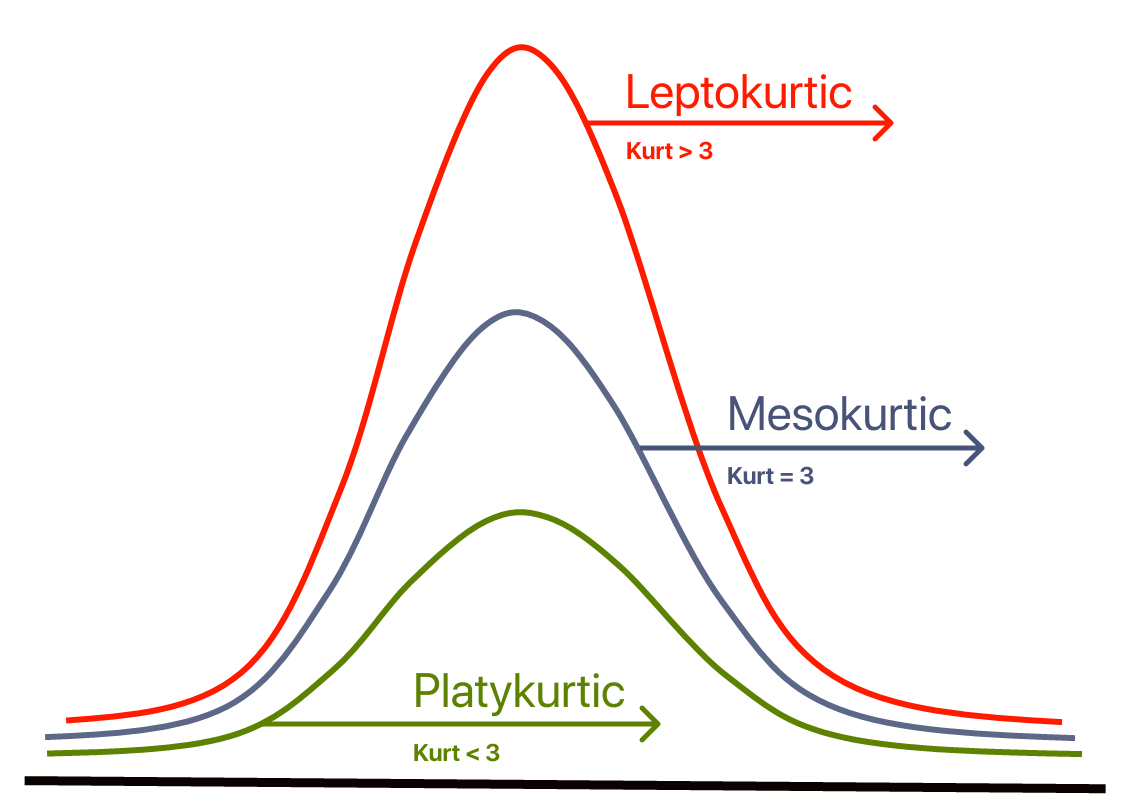
So:

Excess Kurtosis ≈ 0 → Normal distribution
Excess Kurtosis > 0 → Leptokurtic (heavy tails)
Excess Kurtosis < 0 → Platykurtic (light tails)

from scipy.stats import kurtosis
import numpy as np

data = np.array([2, 8, 0, 4, 1, 9, 9, 0])

# By default, it returns excess kurtosis
excess_kurt = kurtosis(data)
print("Excess Kurtosis:", excess_kurt)

# To get regular kurtosis (not excess), set fisher=False
regular_kurt = kurtosis(data, fisher=False)
print("Regular Kurtosis:", regular_kurt)

Excess Kurtosis: -1.6660010752838508
Regular Kurtosis: 1.3339989247161492

Interquartile Kurtosis¶

IQR Kurtosis is a robust, non-parametric measure of kurtosis that focuses on the tails of the distribution using interquartile ranges. It is particularly useful for detecting the intensity of extreme values in data distributions, especially when outliers are present.

The formula for IQR Kurtosis is:

IQR\ Kurtosis = \frac{Q3 - Q1}{2*(C90 - C10)}

(13)

Where:

$Q1$ is the first quartile (25th percentile),
$Q3$ is the third quartile (75th percentile),
$C90$ is the 90th percentile,
$C10$ is the 10th percentile.

Interpretation:

IQR Kurtosis differs from traditional kurtosis in its interpretation. While traditional kurtosis focuses on the intensity of the tails of a distribution (e.g., heavy or light tails), IQR Kurtosis is a robust measure that emphasizes the relative spread of the interquartile range (IQR) and the symmetry of the distribution around the median.

Your turn¶

Try to calculate the IQR Kurtosis coefficient for the sample data:

mydata = [3, 7, 8, 5, 12, 14, 21, 13, 18]
# Your code here

Summary statistics¶

A great tool for creating elegant summaries of descriptive statistics in Markdown format (ideal for Jupyter Notebooks) is pandas, especially in combination with the .describe() function and tabulate.

Example with pandas + tabulate (a nice table in Markdown):

from scipy.stats import skew, kurtosis
from tabulate import tabulate

def markdown_summary(df, round_decimals=3):
    summary = df.describe().T  # transpose so that the variables are in rows
    # Add skewness and kurtosis
    summary['Skewness'] = df.skew()
    summary['Kurtosis'] = df.kurt()
    # Rounding up the results
    summary = summary.round(round_decimals)
    # Nice summary table!
    return tabulate(summary, headers='keys', tablefmt='github')

# We select only the numerical columns for analysis:
quantitative = df_pokemon.select_dtypes(include='number')

# We use our function:
print(markdown_summary(quantitative))

|            |   count |    mean |     std |   min |    25% |   50% |    75% |   max |   Skewness |   Kurtosis |
|------------|---------|---------|---------|-------|--------|-------|--------|-------|------------|------------|
| #          |     800 | 362.814 | 208.344 |     1 | 184.75 | 364.5 | 539.25 |   721 |     -0.001 |     -1.166 |
| Total      |     800 | 435.102 | 119.963 |   180 | 330    | 450   | 515    |   780 |      0.153 |     -0.507 |
| HP         |     800 |  69.259 |  25.535 |     1 |  50    |  65   |  80    |   255 |      1.568 |      7.232 |
| Attack     |     800 |  79.001 |  32.457 |     5 |  55    |  75   | 100    |   190 |      0.552 |      0.17  |
| Defense    |     800 |  73.842 |  31.184 |     5 |  50    |  70   |  90    |   230 |      1.156 |      2.726 |
| Sp. Atk    |     800 |  72.82  |  32.722 |    10 |  49.75 |  65   |  95    |   194 |      0.745 |      0.298 |
| Sp. Def    |     800 |  71.902 |  27.829 |    20 |  50    |  70   |  90    |   230 |      0.854 |      1.628 |
| Speed      |     800 |  68.278 |  29.06  |     5 |  45    |  65   |  90    |   180 |      0.358 |     -0.236 |
| Generation |     800 |   3.324 |   1.661 |     1 |   2    |   3   |   5    |     6 |      0.014 |     -1.24  |

To make a summary table cross-sectionally (i.e. by group), you need to use the groupby() method on the DataFrame and then, for example, describe() or your own aggregate function.

Let’s say you want to group the data by the ‘Type 1’ column (i.e. e.g. Pokémon type: Fire, Water, etc.) and then summarise the quantitative variables (mean, variance, min, max, etc.).

# Grouping by ‘Type 1’ column and statistical summary of numeric columns:
group_summary = df_pokemon.groupby('Type 1')[quantitative.columns].describe()
print(group_summary)

              #                                                               \
          count        mean         std    min     25%    50%     75%    max   
Type 1                                                                         
Bug        69.0  334.492754  210.445160   10.0  168.00  291.0  543.00  666.0   
Dark       31.0  461.354839  176.022072  197.0  282.00  509.0  627.00  717.0   
Dragon     32.0  474.375000  170.190169  147.0  373.00  443.5  643.25  718.0   
Electric   44.0  363.500000  202.731063   25.0  179.75  403.5  489.75  702.0   
Fairy      17.0  449.529412  271.983942   35.0  176.00  669.0  683.00  716.0   
Fighting   27.0  363.851852  218.565200   56.0  171.50  308.0  536.00  701.0   
Fire       52.0  327.403846  226.262840    4.0  143.50  289.5  513.25  721.0   
Flying      4.0  677.750000   42.437209  641.0  641.00  677.5  714.25  715.0   
Ghost      32.0  486.500000  209.189218   92.0  354.75  487.0  709.25  711.0   
Grass      70.0  344.871429  200.264385    1.0  187.25  372.0  496.75  673.0   
Ground     32.0  356.281250  204.899855   27.0  183.25  363.5  535.25  645.0   
Ice        24.0  423.541667  175.465834  124.0  330.25  371.5  583.25  713.0   
Normal     98.0  319.173469  193.854820   16.0  161.25  296.5  483.00  676.0   
Poison     28.0  251.785714  228.801767   23.0   33.75  139.5  451.25  691.0   
Psychic    57.0  380.807018  194.600455   63.0  201.00  386.0  528.00  720.0   
Rock       44.0  392.727273  213.746140   74.0  230.75  362.5  566.25  719.0   
Steel      27.0  442.851852  164.847180  208.0  305.50  379.0  600.50  707.0   
Water     112.0  303.089286  188.440807    7.0  130.00  275.0  456.25  693.0   

          Total              ...   Speed        Generation            \
          count        mean  ...     75%    max      count      mean   
Type 1                       ...                                       
Bug        69.0  378.927536  ...   85.00  160.0       69.0  3.217391   
Dark       31.0  445.741935  ...   98.50  125.0       31.0  4.032258   
Dragon     32.0  550.531250  ...   97.75  120.0       32.0  3.875000   
Electric   44.0  443.409091  ...  101.50  140.0       44.0  3.272727   
Fairy      17.0  413.176471  ...   60.00   99.0       17.0  4.117647   
Fighting   27.0  416.444444  ...   86.00  118.0       27.0  3.370370   
Fire       52.0  458.076923  ...   96.25  126.0       52.0  3.211538   
Flying      4.0  485.000000  ...  121.50  123.0        4.0  5.500000   
Ghost      32.0  439.562500  ...   84.25  130.0       32.0  4.187500   
Grass      70.0  421.142857  ...   80.00  145.0       70.0  3.357143   
Ground     32.0  437.500000  ...   90.00  120.0       32.0  3.156250   
Ice        24.0  433.458333  ...   80.00  110.0       24.0  3.541667   
Normal     98.0  401.683673  ...   90.75  135.0       98.0  3.051020   
Poison     28.0  399.142857  ...   77.00  130.0       28.0  2.535714   
Psychic    57.0  475.947368  ...  104.00  180.0       57.0  3.385965   
Rock       44.0  453.750000  ...   70.00  150.0       44.0  3.454545   
Steel      27.0  487.703704  ...   70.00  110.0       27.0  3.851852   
Water     112.0  430.455357  ...   82.00  122.0      112.0  2.857143   

                                               
               std  min   25%  50%   75%  max  
Type 1                                         
Bug       1.598433  1.0  2.00  3.0  5.00  6.0  
Dark      1.353609  2.0  3.00  5.0  5.00  6.0  
Dragon    1.431219  1.0  3.00  4.0  5.00  6.0  
Electric  1.604697  1.0  2.00  4.0  4.25  6.0  
Fairy     2.147160  1.0  2.00  6.0  6.00  6.0  
Fighting  1.800601  1.0  1.50  3.0  5.00  6.0  
Fire      1.850665  1.0  1.00  3.0  5.00  6.0  
Flying    0.577350  5.0  5.00  5.5  6.00  6.0  
Ghost     1.693203  1.0  3.00  4.0  6.00  6.0  
Grass     1.579173  1.0  2.00  3.5  5.00  6.0  
Ground    1.588454  1.0  1.75  3.0  5.00  5.0  
Ice       1.473805  1.0  2.75  3.0  5.00  6.0  
Normal    1.575407  1.0  2.00  3.0  4.00  6.0  
Poison    1.752927  1.0  1.00  1.5  4.00  6.0  
Psychic   1.644845  1.0  2.00  3.0  5.00  6.0  
Rock      1.848375  1.0  2.00  3.0  5.00  6.0  
Steel     1.350319  2.0  3.00  3.0  5.00  6.0  
Water     1.558800  1.0  1.00  3.0  4.00  6.0  

[18 rows x 72 columns]

Cross-sectional analysis¶

Let’s try to calculate all those statistics by group i.e. perform descriptive analysis for Attack points by Legendary (for legendary and not legendary pokemons.)

grouped_attack = df_pokemon.groupby('Legendary')['Attack']
grouped_summary = grouped_attack.describe()
# let's add skewness and kurtosis now:
grouped_summary['Skewness'] = grouped_attack.apply(lambda x: x.skew())
grouped_summary['Kurtosis'] = grouped_attack.apply(lambda x: x.kurt())
from tabulate import tabulate
print(tabulate(grouped_summary, headers='keys', tablefmt='github'))  #summary in markdown table now

| Legendary   |   count |     mean |     std |   min |   25% |   50% |   75% |   max |   Skewness |   Kurtosis |
|-------------|---------|----------|---------|-------|-------|-------|-------|-------|------------|------------|
| False       |     735 |  75.6694 | 30.4902 |     5 |  54.5 |    72 |    95 |   185 |   0.523333 |   0.145037 |
| True        |      65 | 116.677  | 30.348  |    50 | 100   |   110 |   131 |   190 |   0.50957  |  -0.18957  |

Your turn!¶

Add some cross-sectional plots and try to interpret the results.

# your plots and comments here

Quiz answers on measurement scales:¶

Data Wrangling & Cleansing, Visualization & Analysis with Python.

Data visualization, pt. 3 (principles)

Data Wrangling & Cleansing, Visualization & Analysis with Python.

Bivariate Statistics

Looking ahead: April Week 4, May Week 1¶

Measurement scales¶

Table: Measurement scales in statistics¶

Quiz: measurement scales in statistics.¶

1. Which scale enables ordering of data, but does not have equal spacing?¶

2. An example of a variable on the nominal scale is:¶

3. Which scale does not have absolute zero, but has equal spacing?¶

4. What operations are allowed on variables on an ordinal scale?¶

5. The variable “class” in the Titanic set (First, Second, Third) is an example:¶

Descriptive statistics¶

This week¶

Central tendency¶

Why is this useful?¶

Arithmetic average¶

numpy.mean¶

scipy.stats.tmean¶

Calculating the average of a pandas column.¶

Your turn¶

Average and skewness¶

Your turn¶

Your turn¶

Summary of the first part¶

Median¶

Comparison of median and average.¶

Your turn¶

Mode¶

mode() returns multiple values?¶

Measures of central tendency - summary¶

Quantiles¶

Definition¶

Formula (for an ordered data set)¶

Example - we calculate step by step:¶

Deciles¶

Percentiles¶

Quantiles - summary¶

Example - calculations of quantiles¶

Your turn!¶

Variability¶

The mean hides the variance!¶

Volatility detection¶

Range¶

IQR¶

Variance and standard deviation.¶

SD, explained¶

SD calculation in pandas¶

Note on numpy.std!!!¶

Coefficient of variation (CV).¶

Interquartile deviation¶

Your turn!¶

Measures of the shape of the distribution¶

Skewness¶

Negative skewness¶

Zero skewness¶

Positive skewness¶

Your turn¶

Interquartile Skewness¶

Your turn¶

Kurtosis¶

Reference range for kurtosis¶

Mesocurve¶

Platykurtic curve¶

Leptokurtic curve¶

Interquartile Kurtosis¶

Your turn¶

Summary statistics¶

Cross-sectional analysis¶

Your turn!¶

Quiz answers on measurement scales:¶

5. The variable `“class”` in the Titanic set (`First`, `Second`, `Third`) is an example:¶

`numpy.mean`¶

`scipy.stats.tmean`¶

Calculating the `average` of a `pandas` column.¶

Comparison of `median` and `average`.¶

`mode()` returns multiple values?¶

The `mean` hides the variance!¶

SD calculation in `pandas`¶

Note on `numpy.std`!!!¶