Data visualization, pt. 2 (seaborn)

Goals of this exercise¶

Introducting seaborn.
Putting seaborn into practice:
- Univariate plots (histograms).
- Bivariate continuous plots (scatterplots and line plots).
- Bivariate categorical plots (bar plots, box plots, and strip plots).

Introducing `seaborn`¶

What is `seaborn`?¶

seaborn is a data visualization library based on matplotlib.

In general, it’s easier to make nice-looking graphs with seaborn.
The trade-off is that matplotlib offers more flexibility.

import seaborn as sns ### importing seaborn
import pandas as pd
import matplotlib.pyplot as plt ## just in case we need it
import numpy as np

%matplotlib inline 
%config InlineBackend.figure_format = 'retina'

The `seaborn` hierarchy of plot types¶

We’ll learn more about exactly what this hierarchy means today (and in next lecture).

Example dataset¶

Today we’ll work with a new dataset, from Gapminder.

Gapminder is an independent Swedish foundation dedicated to publishing and analyzing data to correct misconceptions about the world.
Between 1952-2007, has data about life_exp, gdp_cap, and population.

df_gapminder = pd.read_csv("data/gapminder_full.csv")

df_gapminder.head(2)

df_gapminder.shape

(1704, 6)

Univariate plots¶

A univariate plot is a visualization of only a single variable, i.e., a distribution.

We’ve produced histograms with plt.hist.
With seaborn, we can use sns.histplot(...).

Rather than use df['col_name'], we can use the syntax:

sns.histplot(data = df, x = col_name)

This will become even more useful when we start making bivariate plots.

# Histogram of life expectancy
sns.histplot(df_gapminder['life_exp']);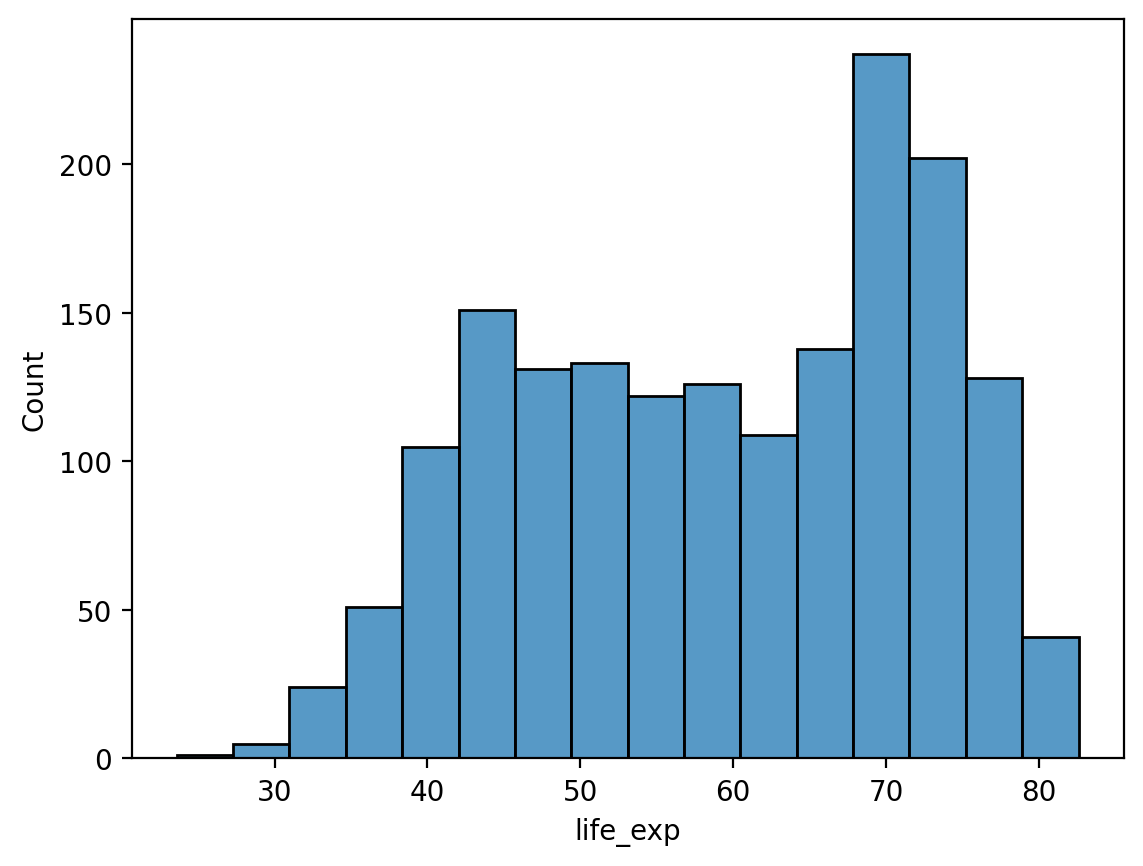

Modifying the number of bins¶

As with plt.hist, we can modify the number of bins.

# Fewer bins
sns.histplot(data = df_gapminder, x = 'life_exp', bins = 10, alpha = .6);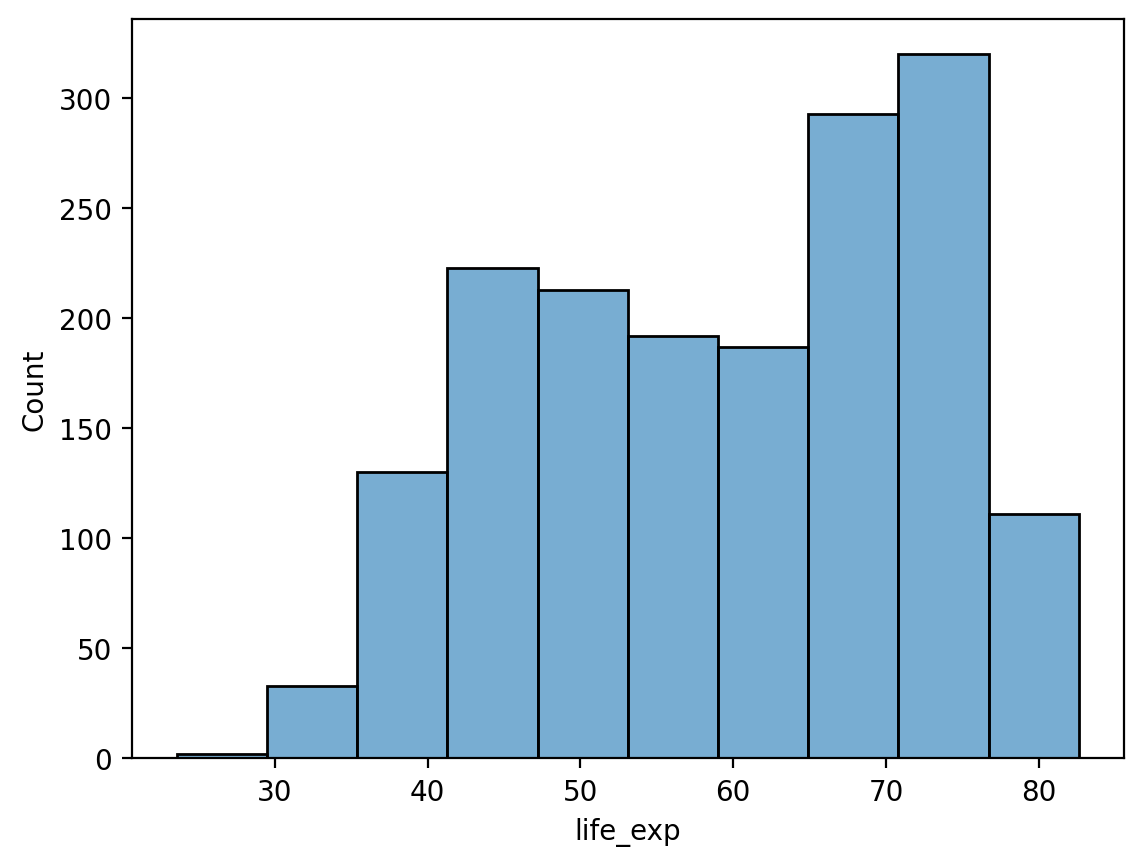

# Many more bins!
sns.histplot(data = df_gapminder, x = 'life_exp', bins = 100, alpha = .6);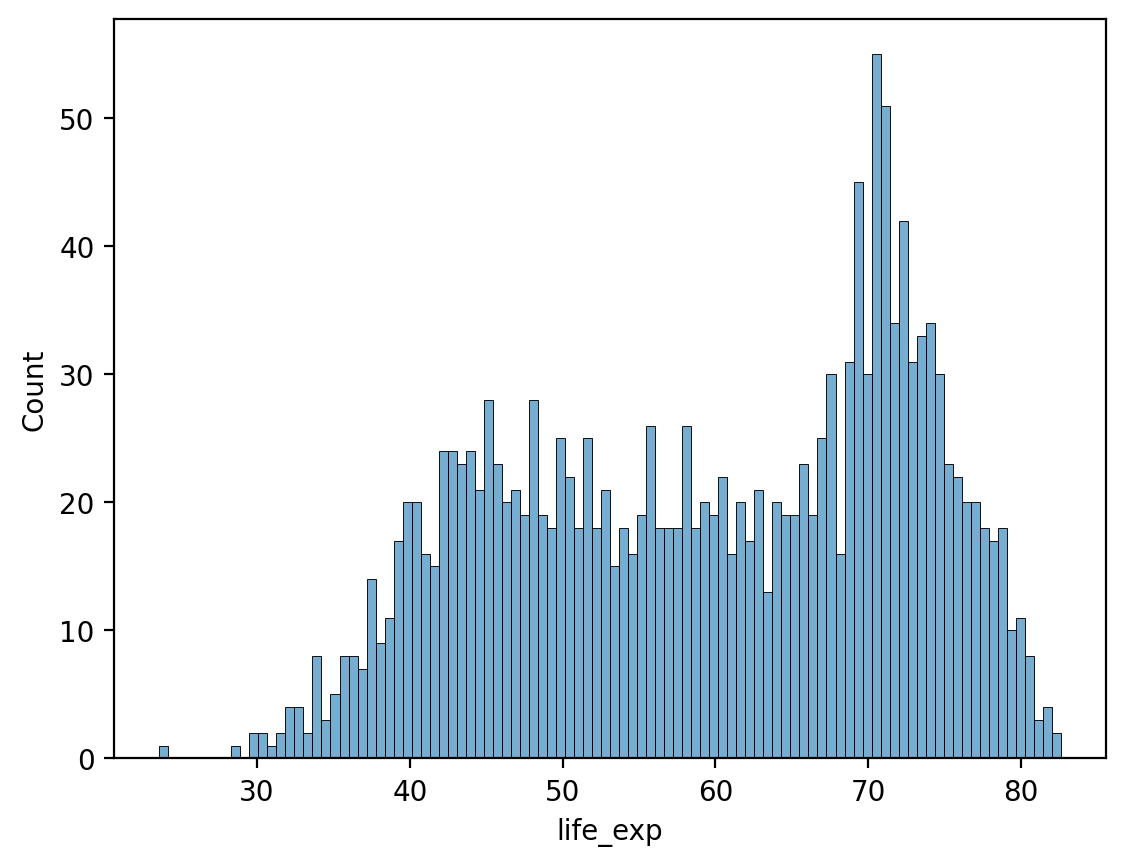

Modifying the y-axis with `stat`¶

By default, sns.histplot will plot the count in each bin. However, we can change this using the stat parameter:

probability: normalize such that bar heights sum to 1.
percent: normalize such that bar heights sum to 100.
density: normalize such that total area sums to 1.

# Note the modified y-axis!
sns.histplot(data = df_gapminder, x = 'life_exp', stat = "percent", alpha = .6);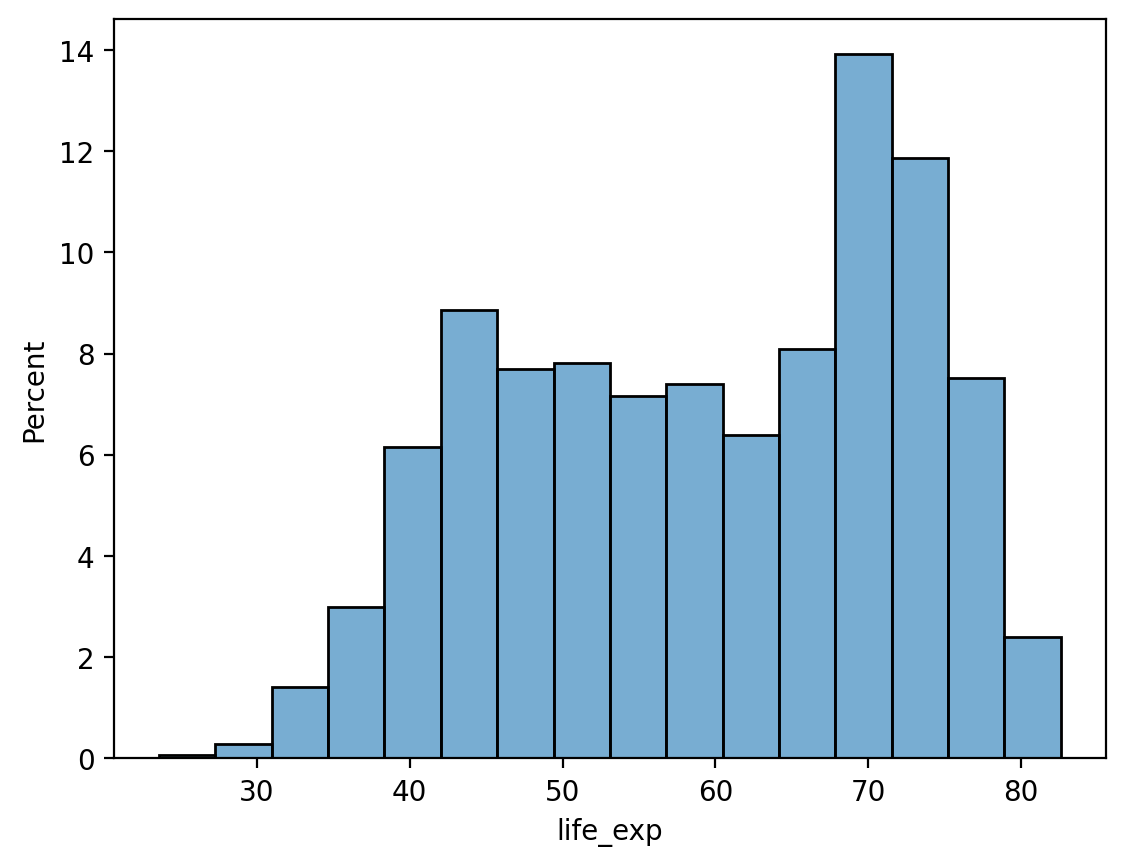

Check-in¶

How would you make a histogram showing the distribution of population values in 2007 alone?

Bonus 1: Modify this graph to show probability, not count.
Bonus 2: What do you notice about this graph, and how might you change it?

### Your code here

Bivariate continuous plots¶

A bivariate continuous plot visualizes the relationship between two continuous variables.

A scatterplot visualizes the relationship between two continuous variables.

Each observation is plotted as a single dot/mark.
The position on the (x, y) axes reflects the value of those variables.

One way to make a scatterplot in seaborn is using sns.scatterplot.

Showing `gdp_cap` by `life_exp`¶

What do we notice about gdp_cap?

sns.scatterplot(data = df_gapminder, x = 'gdp_cap',
               y = 'life_exp', alpha = .3);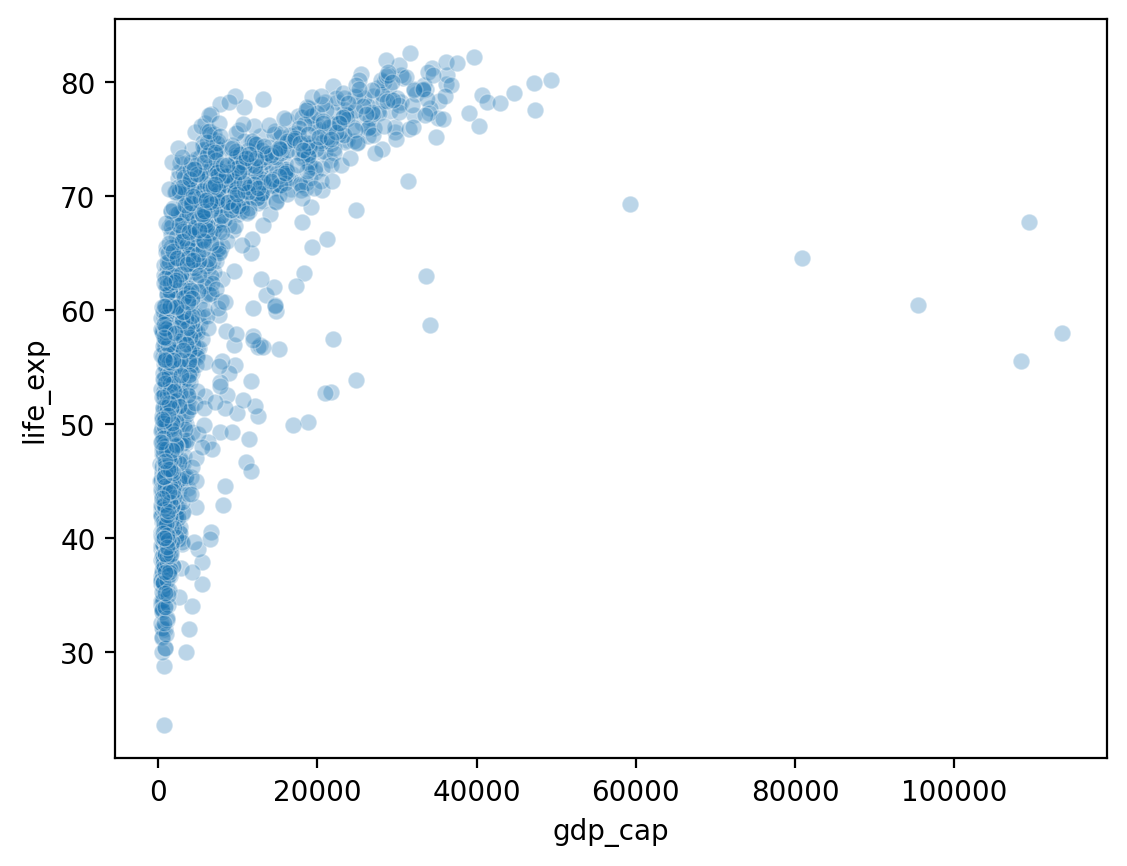

Showing `gdp_cap_log` by `life_exp`¶

## Log GDP
df_gapminder['gdp_cap_log'] = np.log10(df_gapminder['gdp_cap']) 
## Show log GDP by life exp
sns.scatterplot(data = df_gapminder, x = 'gdp_cap_log', y = 'life_exp', alpha = .3);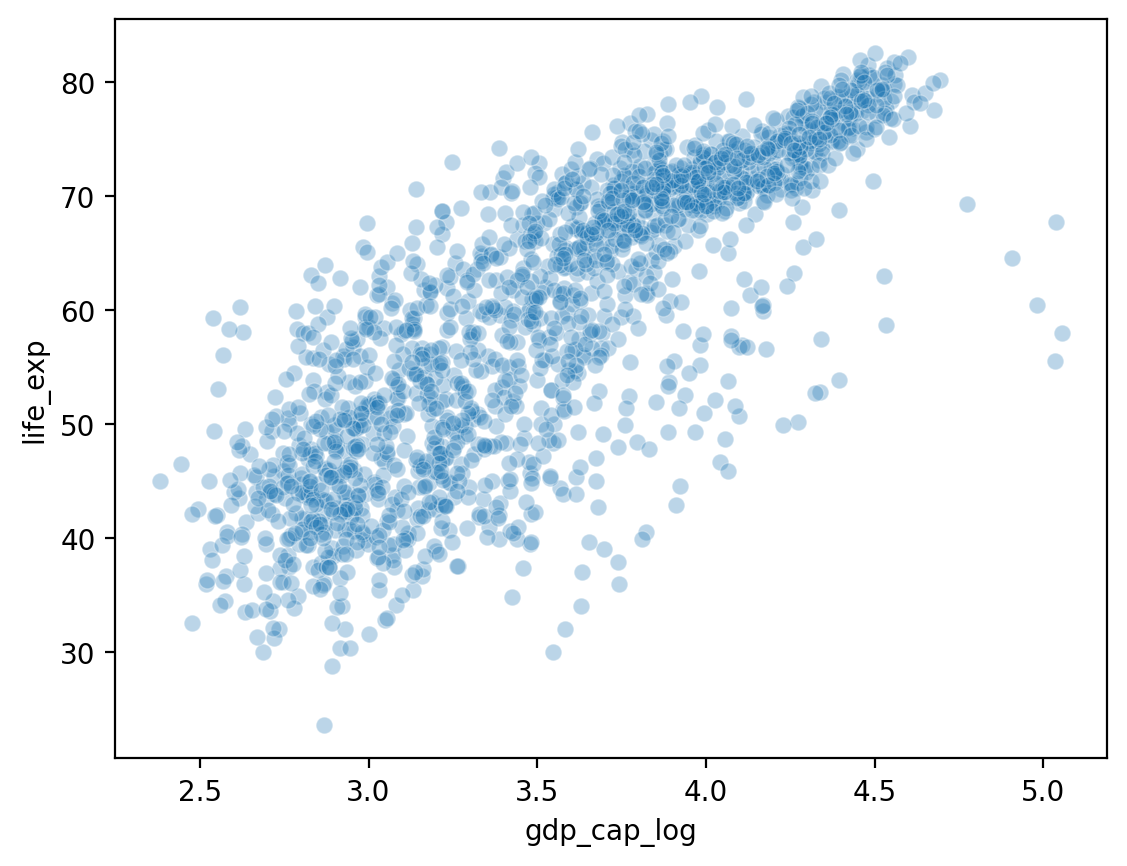

Adding a `hue`¶

What if we want to add a third component that’s categorical, like continent?
seaborn allows us to do this with hue.

## Log GDP
df_gapminder['gdp_cap_log'] = np.log10(df_gapminder['gdp_cap']) 
## Show log GDP by life exp
sns.scatterplot(data = df_gapminder[df_gapminder['year'] == 2007],
               x = 'gdp_cap_log', y = 'life_exp', hue = "continent", alpha = .7);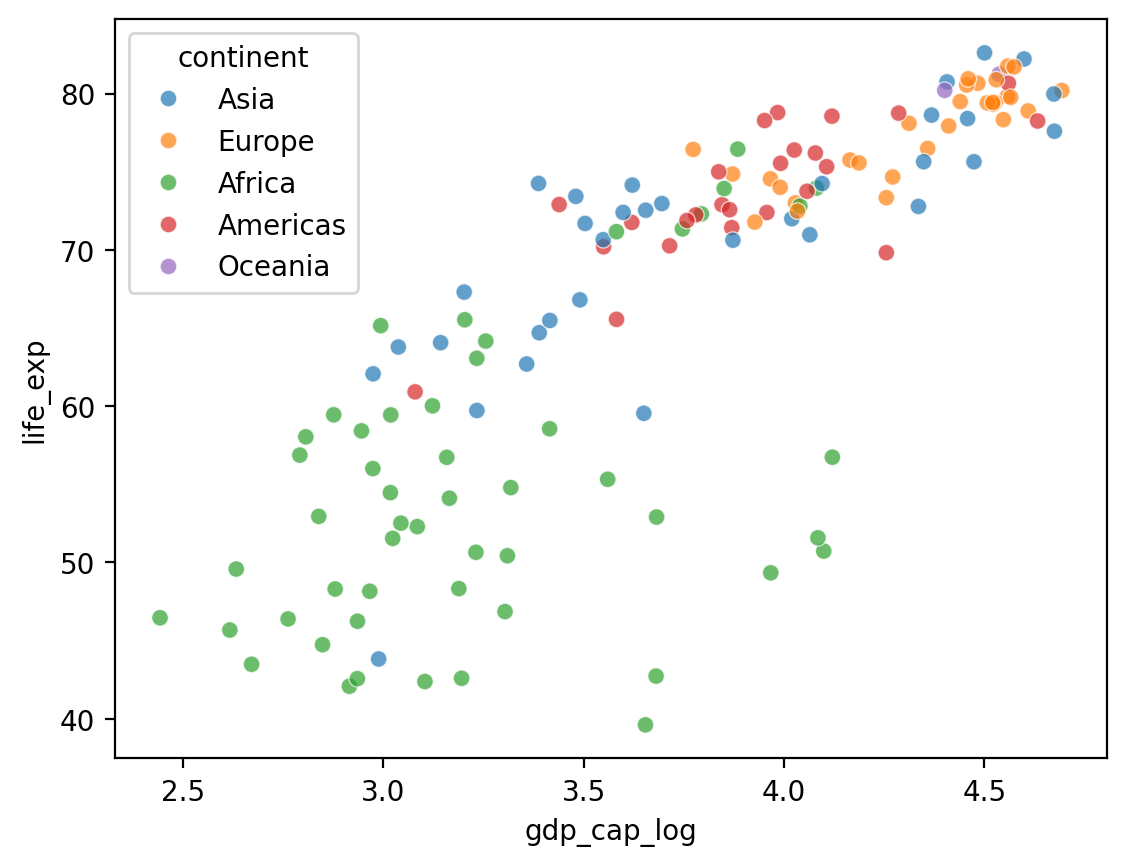

Adding a `size`¶

What if we want to add a fourth component that’s continuous, like population?
seaborn allows us to do this with size.

## Log GDP
df_gapminder['gdp_cap_log'] = np.log10(df_gapminder['gdp_cap']) 
## Show log GDP by life exp
sns.scatterplot(data = df_gapminder[df_gapminder['year'] == 2007],
               x = 'gdp_cap_log', y = 'life_exp',
                hue = "continent", size = 'population', alpha = .7);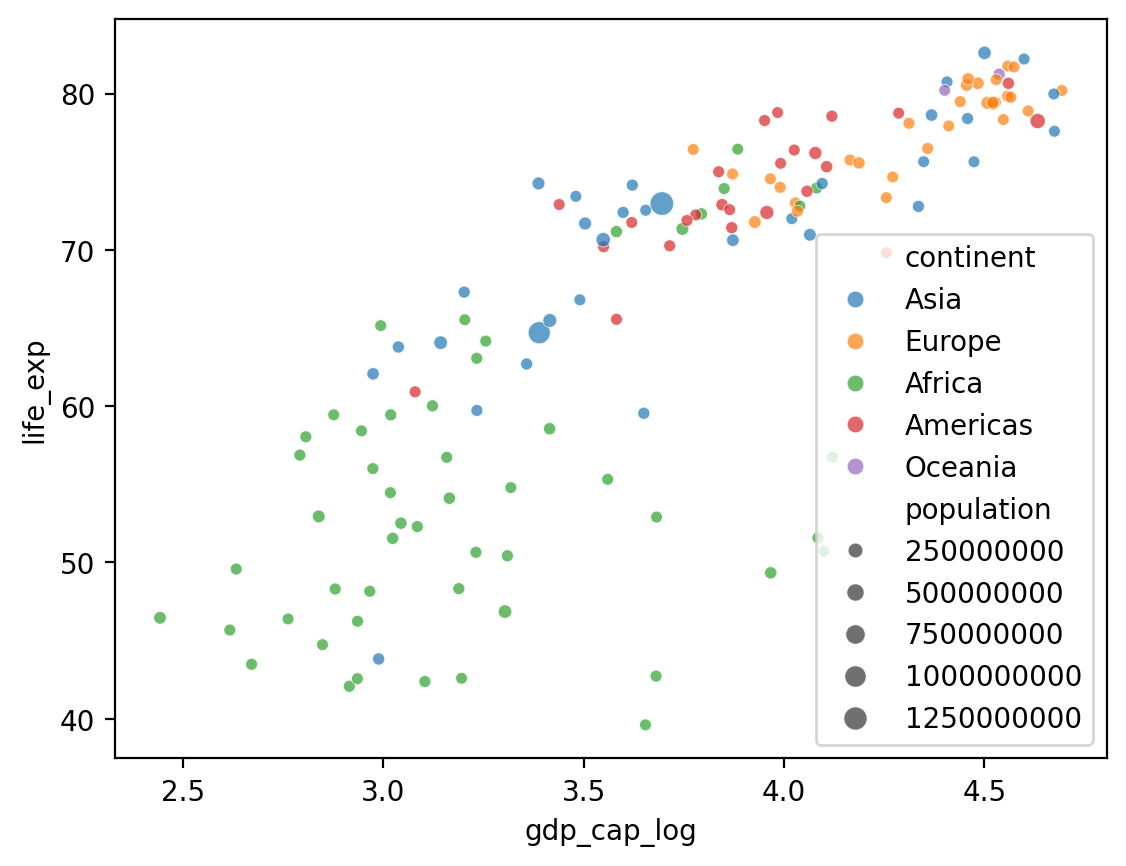

Changing the position of the legend¶

## Show log GDP by life exp
sns.scatterplot(data = df_gapminder[df_gapminder['year'] == 2007],
               x = 'gdp_cap_log', y = 'life_exp',
                hue = "continent", size = 'population', alpha = .7);

plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0);

A lineplot also visualizes the relationship between two continuous variables.

Typically, the position of the line on the y axis reflects the mean of the y-axis variable for that value of x.
Often used for plotting change over time.

One way to make a lineplot in seaborn is using sns.lineplot.

Showing `life_exp` by `year`¶

What general trend do we notice?

sns.lineplot(data = df_gapminder,
             x = 'year',
             y = 'life_exp');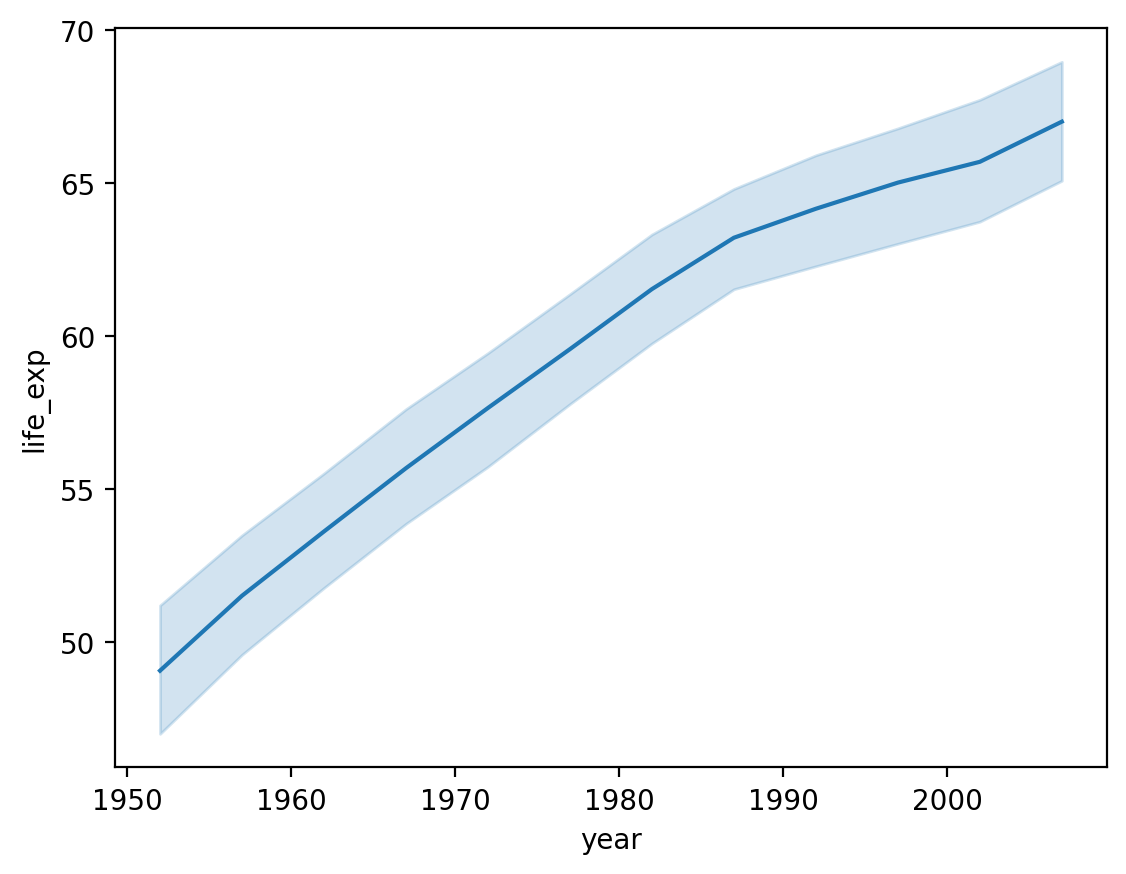

Modifying how error/uncertainty is displayed¶

By default, seaborn.lineplot will draw shading around the line representing a confidence interval.
We can change this with errstyle.

sns.lineplot(data = df_gapminder,
             x = 'year',
             y = 'life_exp',
            err_style = "bars");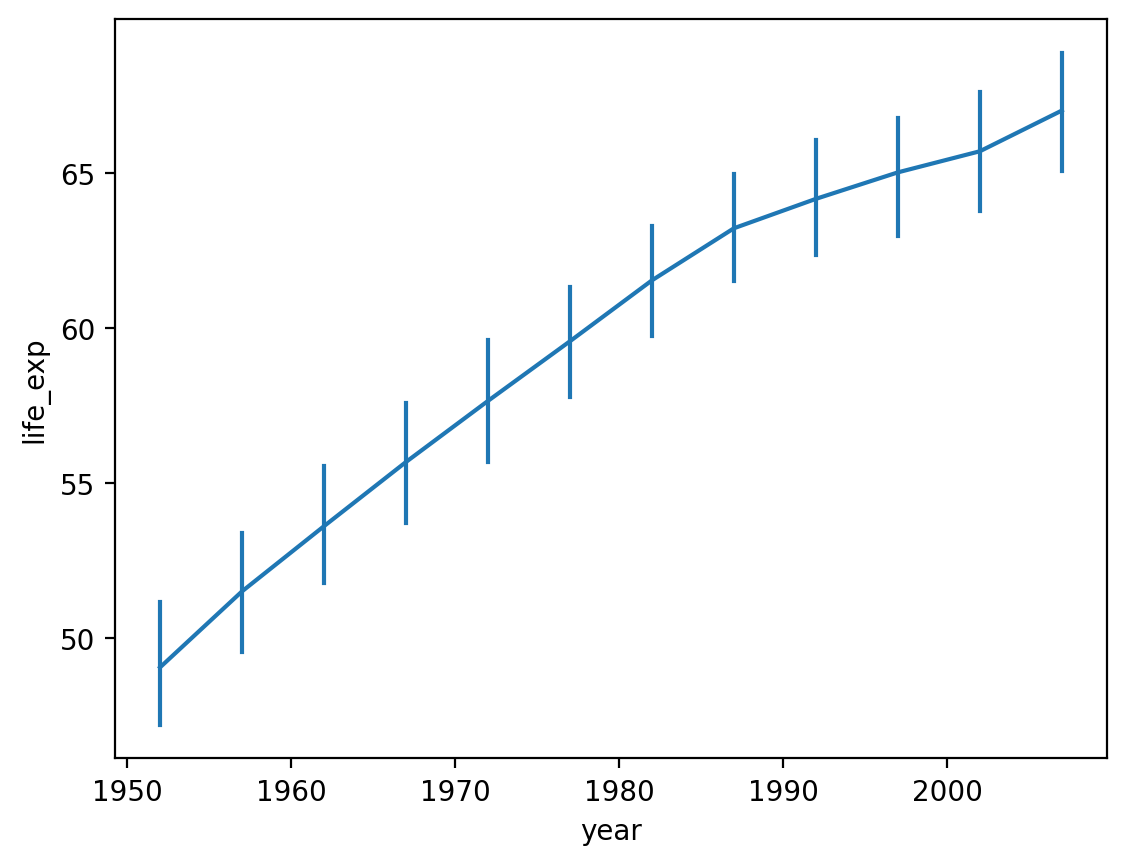

Adding a `hue`¶

We could also show this by continent.
There’s (fortunately) a positive trend line for each continent.

sns.lineplot(data = df_gapminder,
             x = 'year',
             y = 'life_exp',
            hue = "continent")
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0);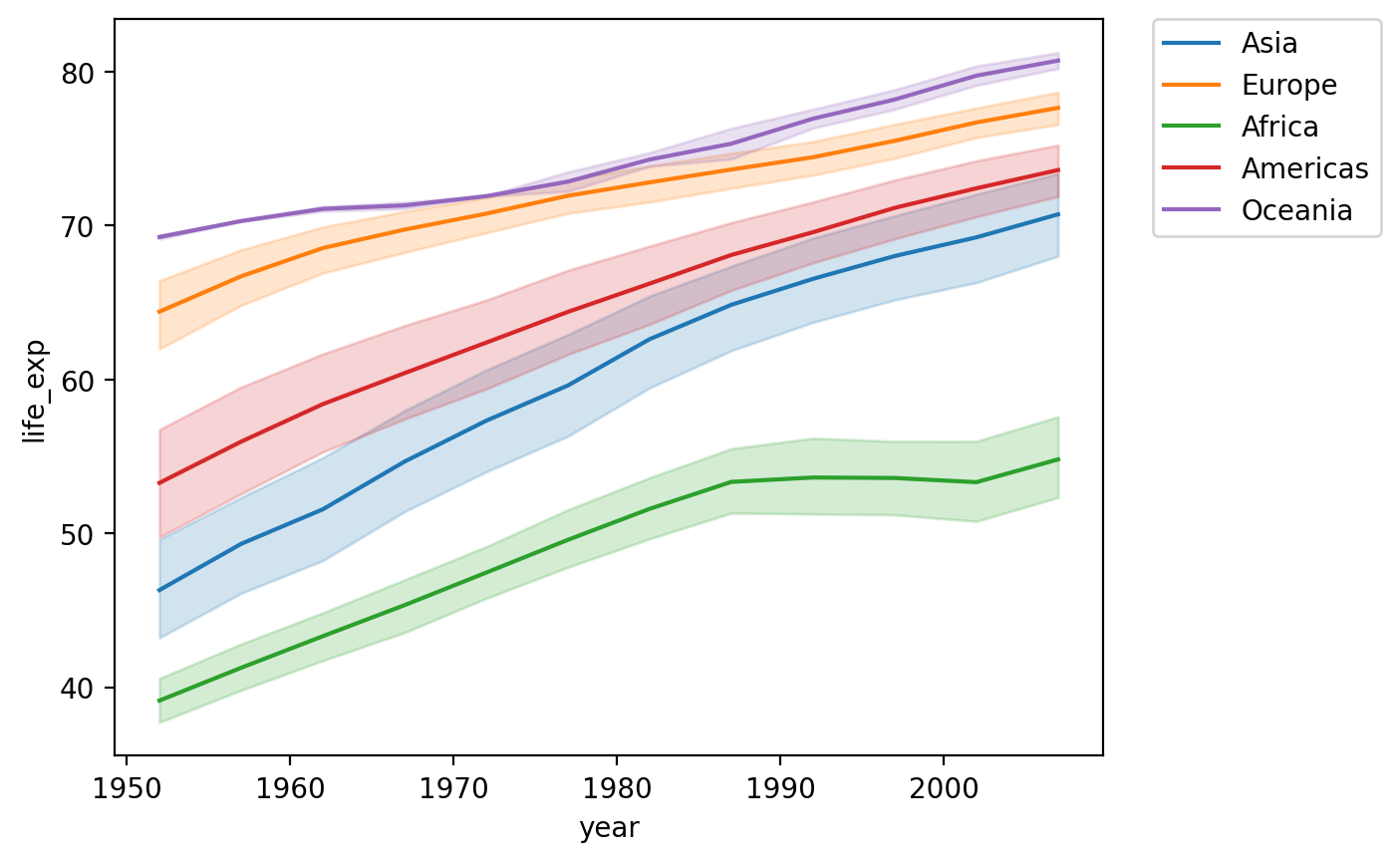

Check-in¶

How would you plot the relationship between year and gdp_cap for countries in the Americas only?

### Your code here

Heteroskedasticity in `gdp_cap` by `year`¶

Heteroskedasticity is when the variance in one variable (e.g., gdp_cap) changes as a function of another variable (e.g., year).
In this case, why do you think that is?

Plotting by country¶

There are too many countries to clearly display in the legend.
But the top two lines are the United States and Canada.
- I.e., two countries have gotten much wealthier per capita, while the others have not seen the same economic growth.

sns.lineplot(data = df_gapminder[df_gapminder['continent']=="Americas"],
             x = 'year', y = 'gdp_cap', hue = "country", legend = None);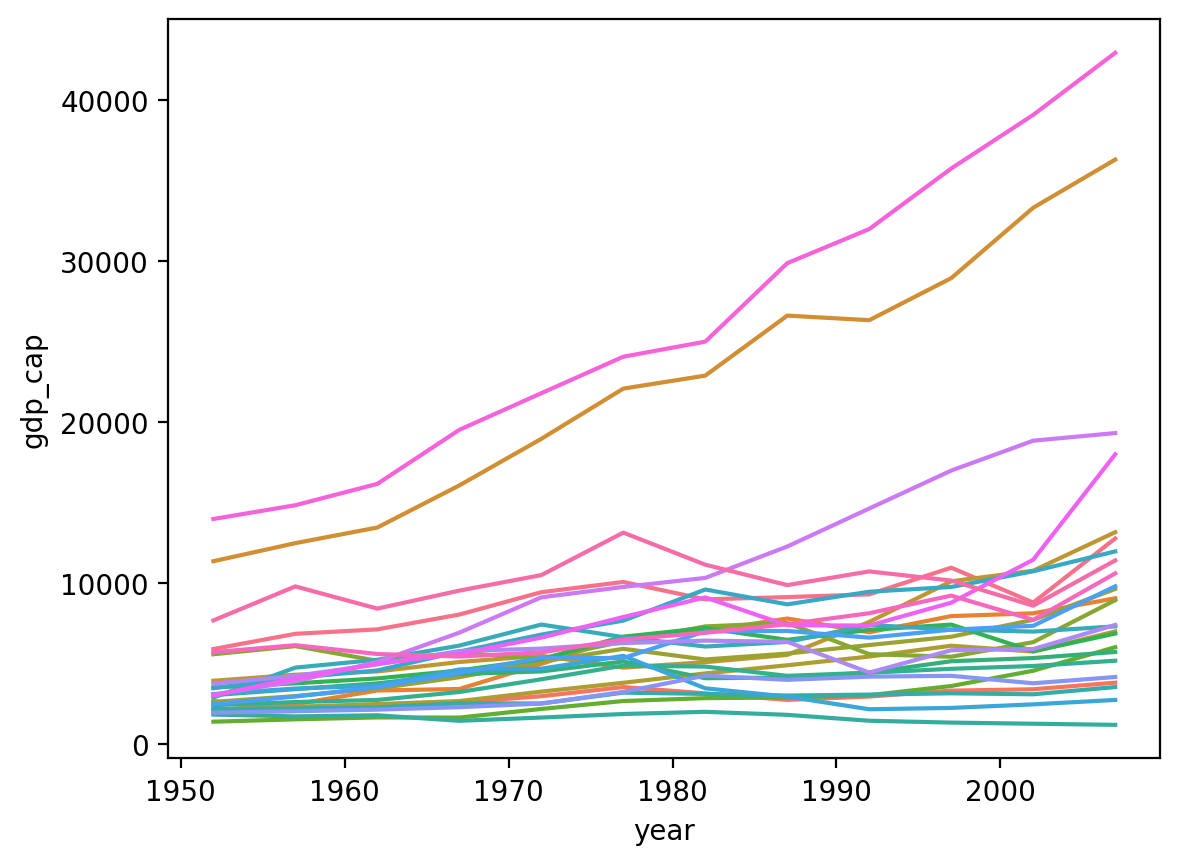

Using `relplot`¶

relplot allows you to plot either line plots or scatter plots using kind.
relplot also makes it easier to facet (which we’ll discuss momentarily).

sns.relplot(data = df_gapminder, x = "year", y = "life_exp", kind = "line");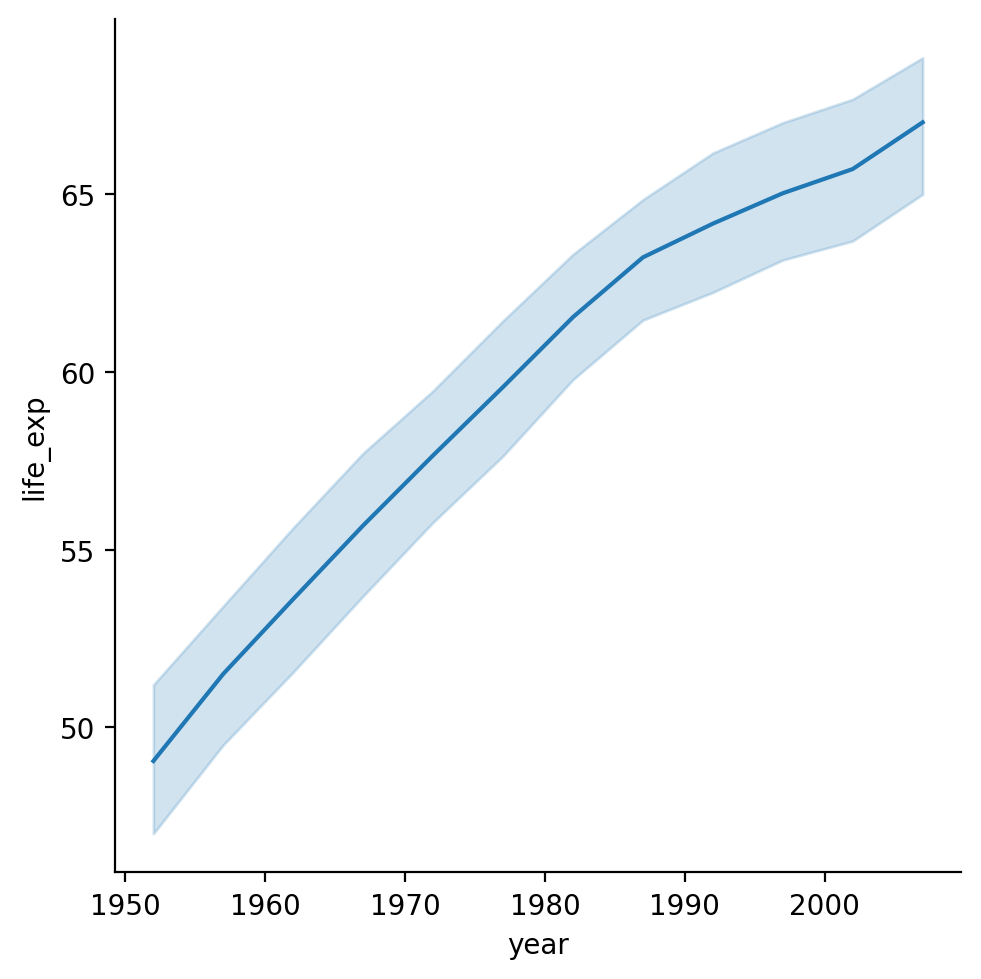

Faceting into `rows` and `cols`¶

We can also plot the same relationship across multiple “windows” or facets by adding a rows/cols parameter.

sns.relplot(data = df_gapminder, x = "year", y = "life_exp", kind = "line", 
            col = "continent");

Bivariate categorical plots¶

A bivariate categorical plot visualizes the relationship between one categorical variable and one continuous variable.

Example dataset¶

Here, we’ll return to our Pokemon dataset, which has more examples of categorical variables.

df_pokemon = pd.read_csv("data/pokemon.csv")

A barplot visualizes the relationship between one continuous variable and a categorical variable.

The height of each bar generally indicates the mean of the continuous variable.
Each bar represents a different level of the categorical variable.

With seaborn, we can use the function sns.barplot.

Average `Attack` by `Legendary` status¶

sns.barplot(data = df_pokemon,
           x = "Legendary", y = "Attack");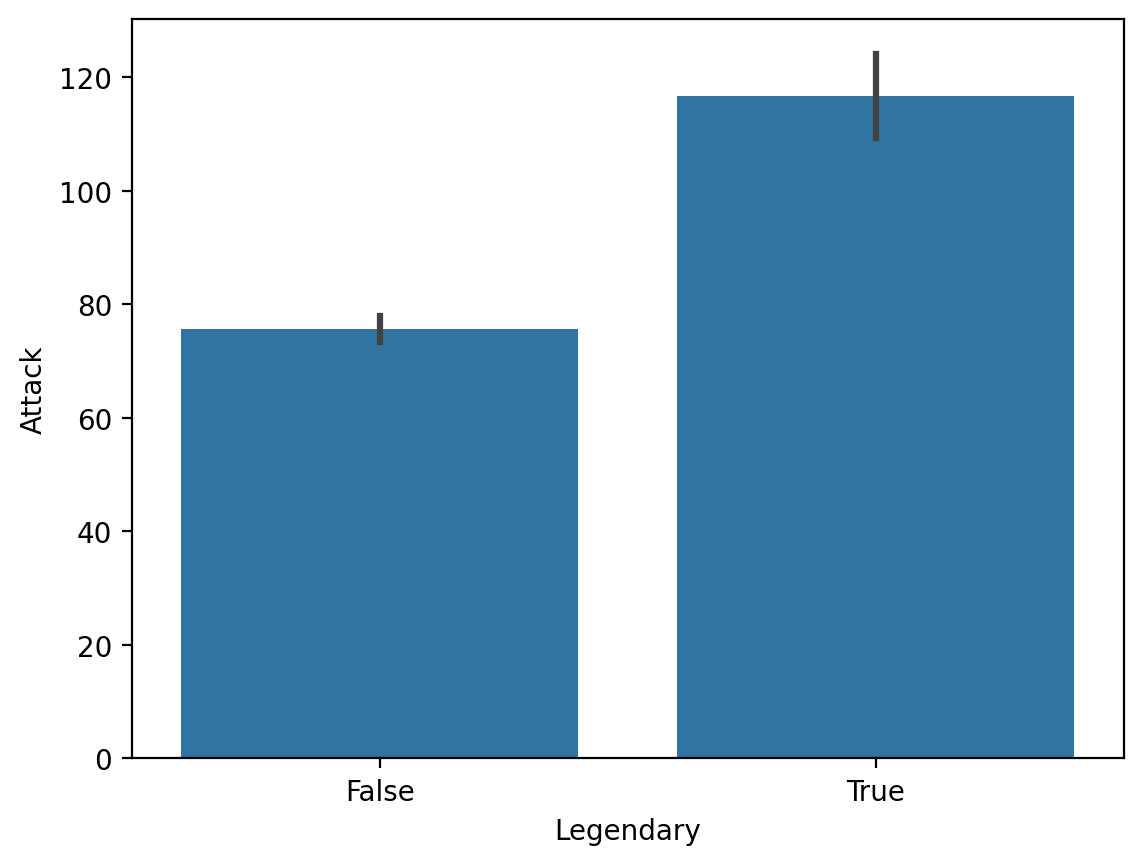

Average `Attack` by `Type 1`¶

Here, notice that I make the figure bigger, to make sure the labels all fit.

plt.figure(figsize=(15,4))
sns.barplot(data = df_pokemon,
           x = "Type 1", y = "Attack");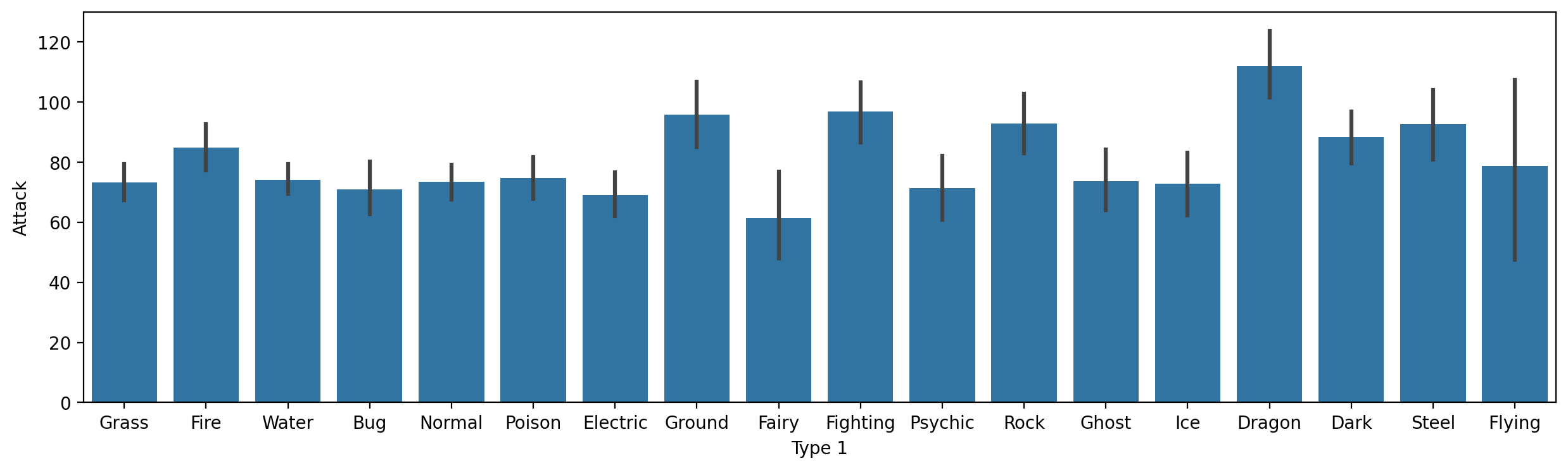

Check-in¶

How would you plot HP by Type 1?

### Your code here

Modifying `hue`¶

As with scatterplot and lineplot, we can change the hue to give further granularity.

E.g., HP by Type 1, further divided by Legendary status.

plt.figure(figsize=(15,4))
sns.barplot(data = df_pokemon,
           x = "Type 1", y = "HP", hue = "Legendary");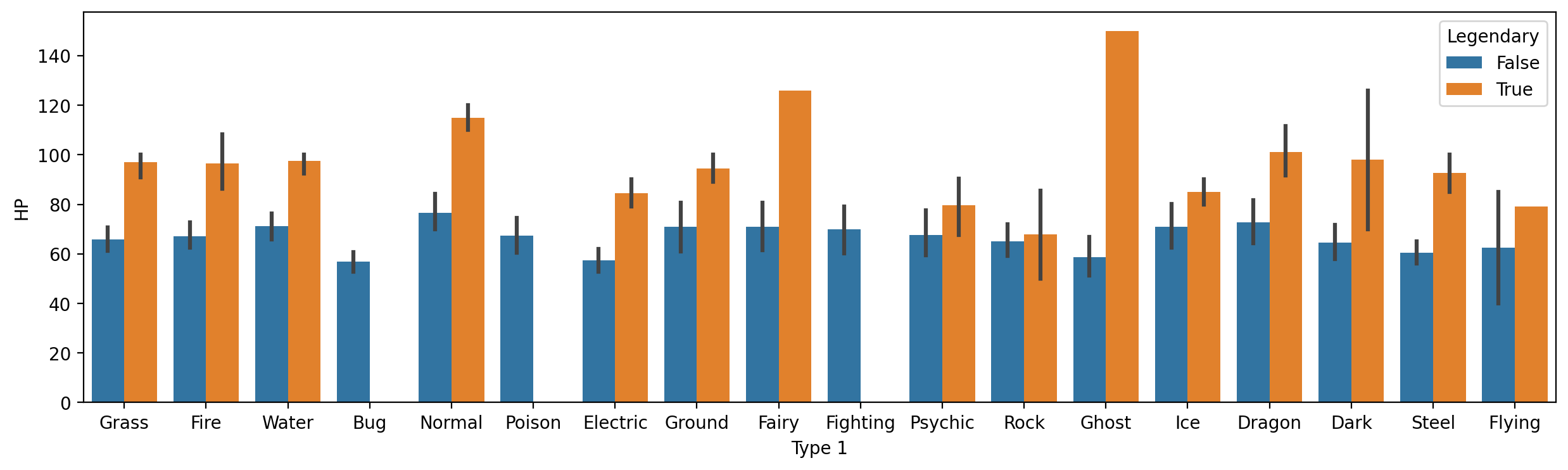

Using `catplot`¶

seaborn.catplot is a convenient function for plotting bivariate categorical data using a range of plot types (bar, box, strip).

sns.catplot(data = df_pokemon, x = "Legendary", 
             y = "Attack", kind = "bar");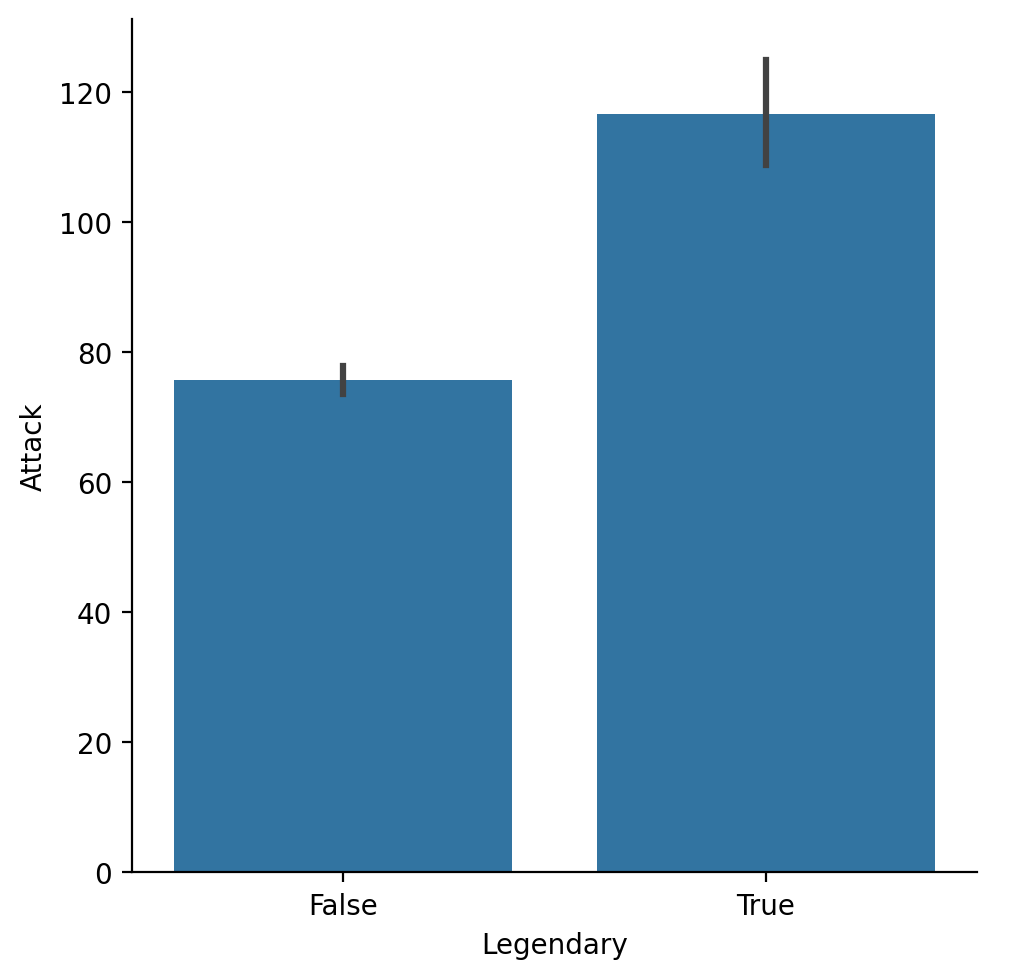

`strip` plots¶

A strip plot shows each individual point (like a scatterplot), divided by a category label.

sns.catplot(data = df_pokemon, x = "Legendary", 
             y = "Attack", kind = "strip", alpha = .5);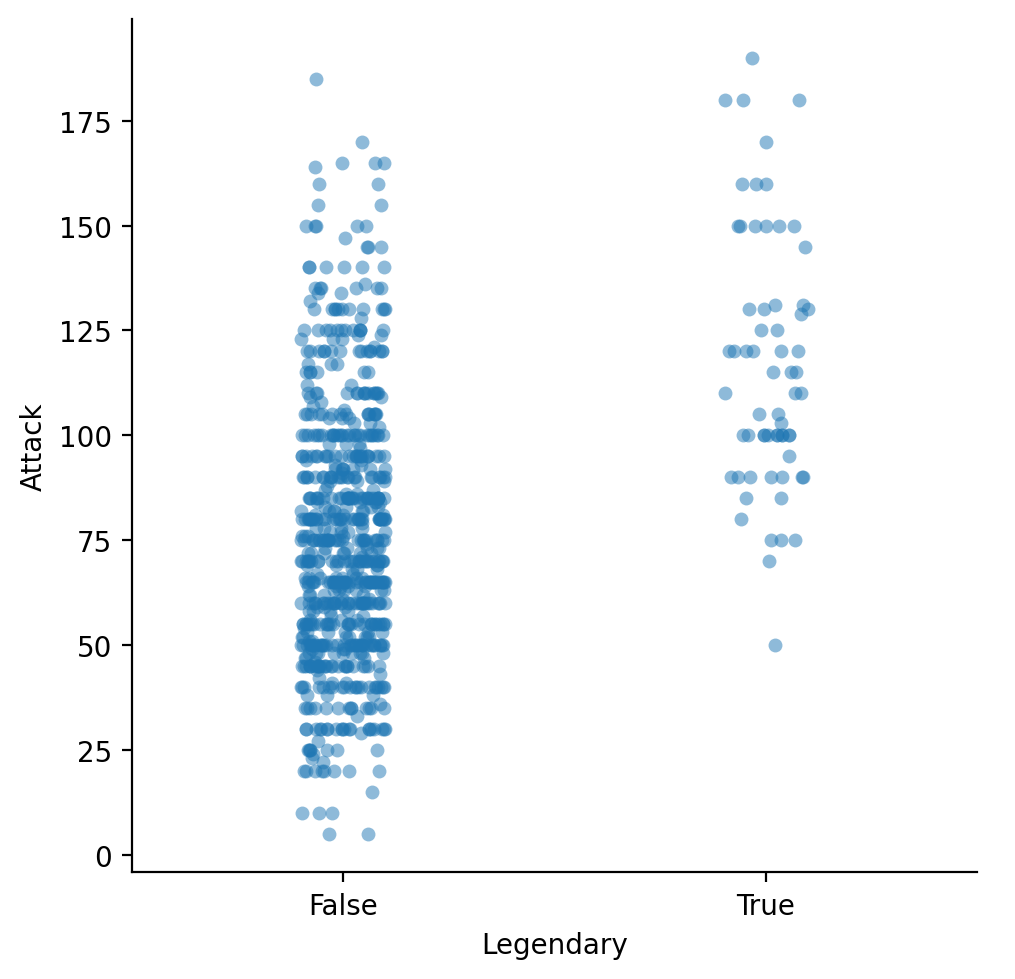

Adding a `mean` to our `strip` plot¶

We can plot two graphs at the same time, showing both the individual points and the means.

sns.catplot(data = df_pokemon, x = "Legendary", 
             y = "Attack", kind = "strip", alpha = .1)
sns.pointplot(data = df_pokemon, x = "Legendary", 
             y = "Attack", hue = "Legendary");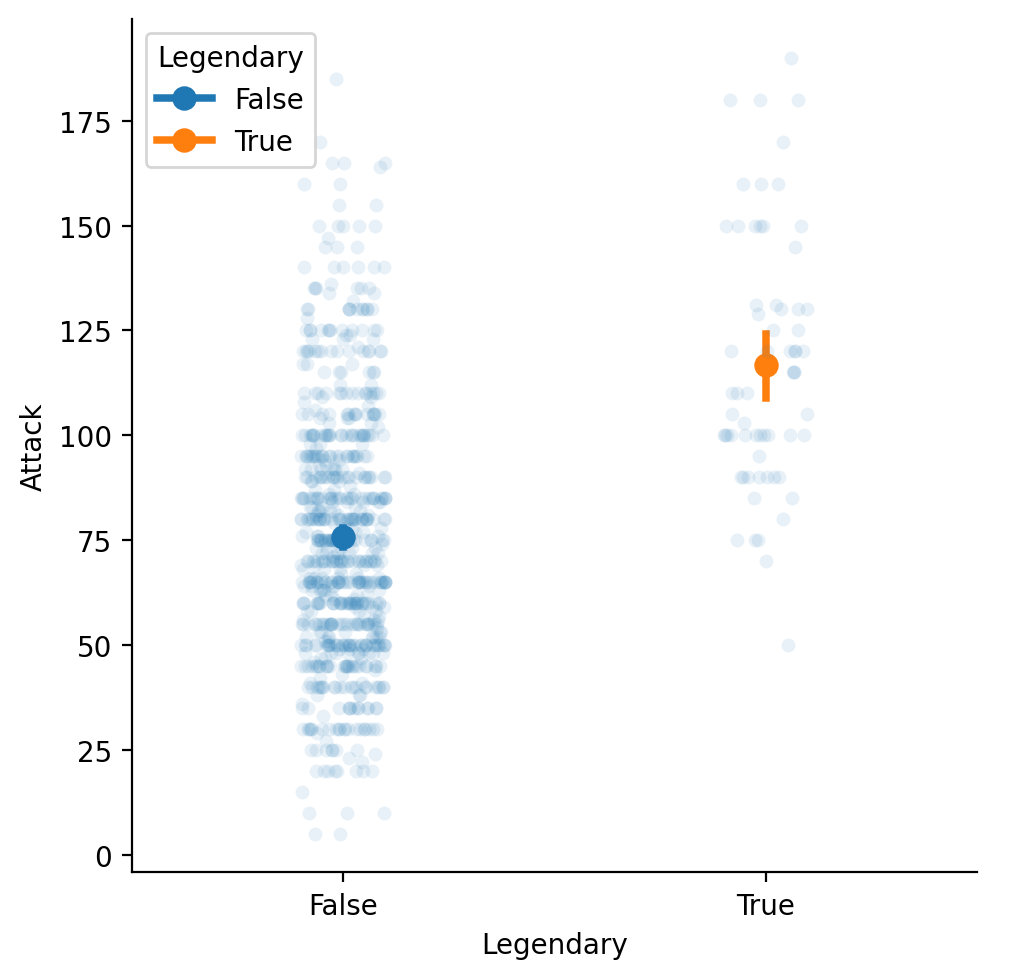

`box` plots¶

A box plot shows the interquartile range (the middle 50% of the data), along with the minimum and maximum.

A typical boxplot contains several components that are part of its anatomy:

Median: This is the middle value of the data, represented by a line in the boxplot.
Boxes: These represent the interquartile range (IQR) of the data, which represents the range between Q1 and Q3. The bottom and top edges represent Q1 and Q3, respectively.
Whiskers: These are vertical lines that extend from both ends of the box to represent the minimum and maximum values, excluding outliers.
Outliers: These are points outside the whiskers that are considered abnormal or extreme compared to the rest of the data.
Limiters: These are the horizontal lines at the ends of the whiskers, representing minimum and maximum values, including any outliers.

Do the whiskers show the minimum and maximum?

From a statistical point of view - the ends of the whiskers are therefore not min and max - because they do not contain part of the outliers.

Standard rules:

Outliers: These are points outside the whiskers’ range. These values are considered abnormal compared to the rest of the data.
Whiskers range: Whiskers extend to values that are within limits:
- Lower whisker: $Q1 - 1.5 * IQR$
- Upper whisker: $Q3 + 1.5 * IQR$
Extreme outliers: If the values are much further outside the whiskers (e.g., $Q1 - 3 * IQR$ or $Q3 + 3 * IQR$ ), they may be considered extreme outliers.

Why are outliers important?

May indicate errors in data (e.g., typos, measurement errors).
They may represent real but rare events that are worth investigating.
Outliers can significantly affect descriptive statistics, such as the mean, so their identification is crucial in data analysis.

Why 1.5 × IQR?

1.5 × $IQR$ is the standard value used to identify moderate outliers.

The interquartile range (IQR) is the difference between the third quartile (Q3) and the first quartile (Q1), the range within which the middle 50% of the data is located.

Values that fall outside the range:

Lower threshold: $Q1$ - 1.5 × $IQR$
Upper threshold: $Q3$ + 1.5 × $IQR$ are considered outliers.

The 1.5 value was empirically chosen as a reasonable compromise between detecting outliers and ignoring natural fluctuations in the data.

Why 3 × IQR?

3 × $IQR$ is used to identify extreme outliers that are much more distant from the rest of the data.

Outlier values:

Lower threshold: $Q1$ - 3 × $IQR$
Upper threshold: $Q3$ + 3 × $IQR$ are considered extreme outliers.

The 3 × $IQR$ value is more stringent and identifies points that are highly unusual and may indicate data errors or rare events.

sns.catplot(data = df_pokemon, x = "Legendary", 
             y = "Attack", kind = "box");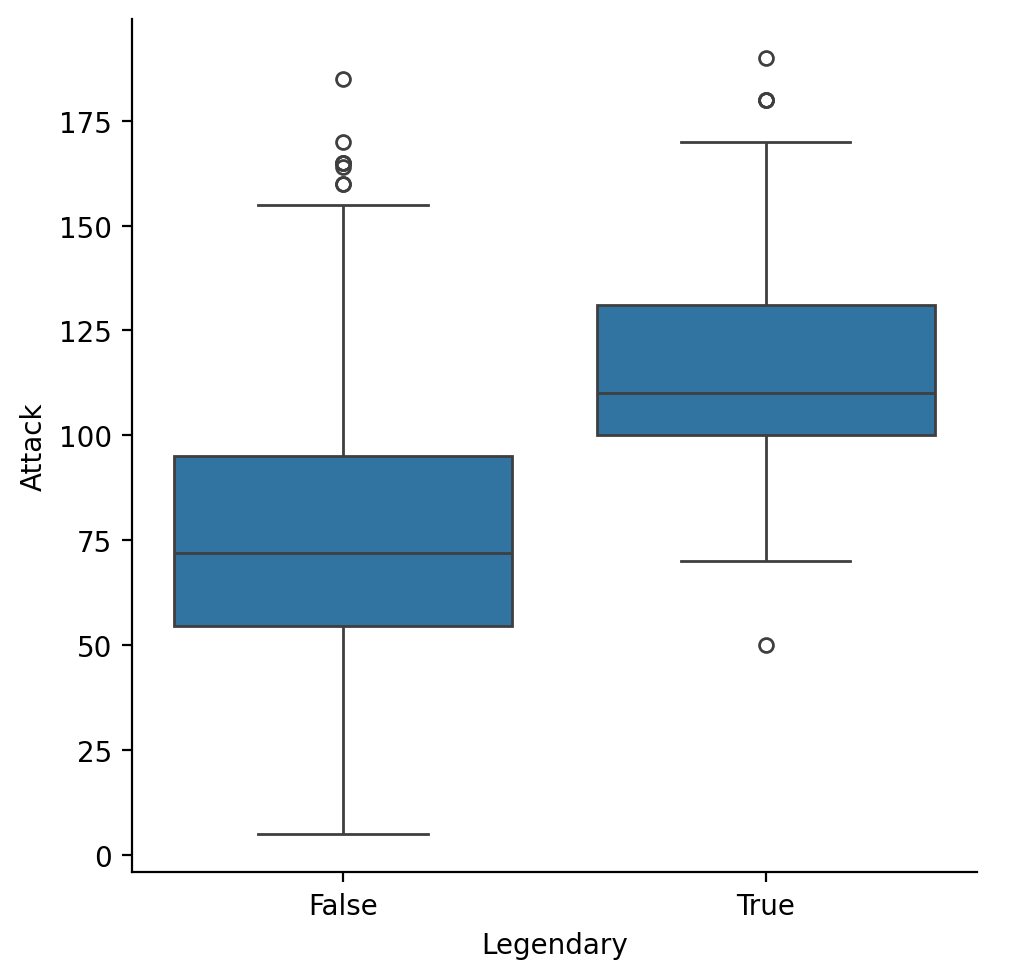

Try to consider converting the boxplots into violin plots.

Conclusion¶

As with our lecture on pyplot, this just scratches the surface.

But now, you’ve had an introduction to:

The seaborn package.
Plotting both univariate and bivariate data.
Creating plots with multiple layers.

Data Wrangling & Cleansing, Visualization & Analysis with Python.

Data visualization in Python (pyplot)

Data Wrangling & Cleansing, Visualization & Analysis with Python.

Data visualization, pt. 3 (principles)

Goals of this exercise¶

Introducing seaborn¶

What is seaborn?¶

The seaborn hierarchy of plot types¶

Example dataset¶

Univariate plots¶

Histograms with sns.histplot¶

Modifying the number of bins¶

Modifying the y-axis with stat¶

Check-in¶

Bivariate continuous plots¶

Scatterplots with sns.scatterplot¶

Showing gdp_cap by life_exp¶

Showing gdp_cap_log by life_exp¶

Adding a hue¶

Adding a size¶

Changing the position of the legend¶

Lineplots with sns.lineplot¶

Showing life_exp by year¶

Modifying how error/uncertainty is displayed¶

Adding a hue¶

Check-in¶

Heteroskedasticity in gdp_cap by year¶

Plotting by country¶

Using relplot¶

Faceting into rows and cols¶

Bivariate categorical plots¶

Example dataset¶

Barplots with sns.barplot¶

Average Attack by Legendary status¶

Average Attack by Type 1¶

Check-in¶

Modifying hue¶

Using catplot¶

strip plots¶

Adding a mean to our strip plot¶

box plots¶

Conclusion¶

Introducing `seaborn`¶

What is `seaborn`?¶

The `seaborn` hierarchy of plot types¶

Histograms with `sns.histplot`¶

Modifying the y-axis with `stat`¶

Scatterplots with `sns.scatterplot`¶

Showing `gdp_cap` by `life_exp`¶

Showing `gdp_cap_log` by `life_exp`¶

Adding a `hue`¶

Adding a `size`¶

Lineplots with `sns.lineplot`¶

Showing `life_exp` by `year`¶

Adding a `hue`¶

Heteroskedasticity in `gdp_cap` by `year`¶

Using `relplot`¶

Faceting into `rows` and `cols`¶

Barplots with `sns.barplot`¶

Average `Attack` by `Legendary` status¶

Average `Attack` by `Type 1`¶

Modifying `hue`¶

Using `catplot`¶

`strip` plots¶

Adding a `mean` to our `strip` plot¶

`box` plots¶